Quadratic polynomial
Encyclopedia
In mathematics, a quadratic polynomial or quadratic is a polynomial
of degree
two, also called second-order polynomial. That means the exponents of the polynomial's variables are no larger than 2. For example, is a quadratic polynomial, while is not.
or complex number
s, but in fact, a polynomial may be defined over any ring
.
". Usually the context will establish which of the two is meant.
Sometimes the word "order" is used with the meaning of "degree", e.g. a second-order polynomial.
x, or multiple variables such as x, y, and z.
where x is the variable, and a, b, and c represent the coefficient
s. In elementary algebra
, such polynomials often arise in the form of a quadratic equation
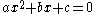. The solutions to this equation are called the roots of the quadratic polynomial, and may be found through factorization
, completing the square
, graphing
, Newton's method
, or through the use of the quadratic formula. Each quadratic polynomial has an associated quadratic function
, whose graph
is a parabola
.
If the polynomial is a polynomial in one variable
, it determines a quadratic function
in one variable. An example is given by f(x) = x2 + x − 2;. The graph
of such a function
is a parabola
(in degenerate cases a line
), and its zeroes can be found by solving the quadratic equation
f(x) = 0.
There are three main forms :
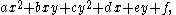
where x and y are the variables and a, b, c, d, e, and f are the coefficients. Such polynomials are fundamental to the study of conic section
s.
Similarly, quadratic polynomials with three or more variables correspond to quadric
surfaces and hypersurface
s. In linear algebra
, quadratic polynomials can be generalized to the notion of a quadratic form
on a vector space
.
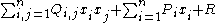
where Q is a symmetric n-dimensional matrix
, P is an n-dimensional vector, and R a constant.
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
of degree
Degree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
two, also called second-order polynomial. That means the exponents of the polynomial's variables are no larger than 2. For example, is a quadratic polynomial, while is not.
Coefficients
The coefficients of a polynomial are often taken to be realQuadratic function
A quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....
or complex number
Complex quadratic polynomial
A complex quadratic polynomial is a quadratic polynomial whose coefficients are complex numbers.-Forms:When the quadratic polynomial has only one variable , one can distinguish its 4 main forms:...
s, but in fact, a polynomial may be defined over any ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
.
Degree
When using the term "quadratic polynomial", authors sometimes mean "having degree exactly 2", and sometimes "having degree at most 2". If the degree is less than 2, this may be called a "degenerate caseDegeneracy (mathematics)
In mathematics, a degenerate case is a limiting case in which a class of object changes its nature so as to belong to another, usually simpler, class....
". Usually the context will establish which of the two is meant.
Sometimes the word "order" is used with the meaning of "degree", e.g. a second-order polynomial.
Variables
A quadratic polynomial may involve a single variableVariable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
x, or multiple variables such as x, y, and z.
The one-variable case
Any single-variable quadratic polynomial may be written aswhere x is the variable, and a, b, and c represent the coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s. In elementary algebra
Elementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
, such polynomials often arise in the form of a quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
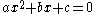. The solutions to this equation are called the roots of the quadratic polynomial, and may be found through factorizationFactorization
In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
, completing the square
Completing the square
In elementary algebra, completing the square is a technique for converting a quadratic polynomial of the formax^2 + bx + c\,\!to the formIn this context, "constant" means not depending on x. The expression inside the parenthesis is of the form ...
, graphing
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
, Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
, or through the use of the quadratic formula. Each quadratic polynomial has an associated quadratic function
Quadratic function
A quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....
, whose graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
is a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
.
If the polynomial is a polynomial in one variable
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
, it determines a quadratic function
Quadratic function
A quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....
in one variable. An example is given by f(x) = x2 + x − 2;. The graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of such a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
(in degenerate cases a line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
), and its zeroes can be found by solving the quadratic equation
Quadratic equation
In mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
f(x) = 0.
There are three main forms :
- general form,
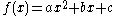. - logistic formLogistic mapThe logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
,
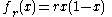, used to study 1DEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
discrete dynamics, - monic and centered formComplex quadratic polynomialA complex quadratic polynomial is a quadratic polynomial whose coefficients are complex numbers.-Forms:When the quadratic polynomial has only one variable , one can distinguish its 4 main forms:...
,
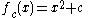, used to study complex dynamicsComplex dynamicsComplex dynamics is the study of dynamical systems defined by iteration of functions on complex number spaces. Complex analytic dynamics is the study of the dynamics of specifically analytic functions.-Techniques:*General** Montel's theorem...
.
Two variables case
Any quadratic polynomial with two variables may be written as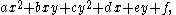where x and y are the variables and a, b, c, d, e, and f are the coefficients. Such polynomials are fundamental to the study of conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
s.
Similarly, quadratic polynomials with three or more variables correspond to quadric
Quadric
In mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
surfaces and hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
s. In linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, quadratic polynomials can be generalized to the notion of a quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
on a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
.
N variables case
In the general case, a quadratic polynomial in n variables x1, ..., xn can be written in the form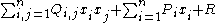where Q is a symmetric n-dimensional matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, P is an n-dimensional vector, and R a constant.
See also
- Periodic points of complex quadratic mappingsPeriodic points of complex quadratic mappingsThis article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the...
- Quadratic equationQuadratic equationIn mathematics, a quadratic equation is a univariate polynomial equation of the second degree. A general quadratic equation can be written in the formax^2+bx+c=0,\,...
- Quadratic functionQuadratic functionA quadratic function, in mathematics, is a polynomial function of the formf=ax^2+bx+c,\quad a \ne 0.The graph of a quadratic function is a parabola whose axis of symmetry is parallel to the y-axis....