CYK algorithm
Encyclopedia
The Cocke–Younger–Kasami (CYK) algorithm (alternatively called CKY) is a parsing
algorithm
for context-free grammar
s. It employs bottom-up parsing
and dynamic programming
.
The standard version of CYK operates only on context-free grammars given in Chomsky normal form
(CNF). However any context-free grammar may be transformed to a CNF grammar expressing the same language .
The importance of the CYK algorithm stems from its high efficiency in certain situations. Using Landau symbols, the worst case running time
of CYK is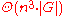
, where n is the length of the parsed string and |G| is the size of the CNF grammar G. This makes it the most efficient parsing algorithm in terms of worst-case asymptotic complexity, although other algorithms exist with better average running time in many practical scenarios.
(CNF), because it tests for possibilities to split the current sequence in half. Any context-free grammar can be represented in CNF using only rules of the forms
and 
.
is as follows:
let the input be a string S consisting of n characters: a1 ... an.
let the grammar contain r nonterminal symbols R1 ... Rr.
This grammar contains the subset Rs which is the set of start symbols.
let P[n,n,r] be an array of booleans. Initialize all elements of P to false.
for each i = 1 to n
for each unit production Rj -> ai
set P[i,1,j] = true
for each i = 2 to n -- Length of span
for each j = 1 to n-i+1 -- Start of span
for each k = 1 to i-1 -- Partition of span
for each production RA -> RB RC
if P[j,k,B] and P[j+k,i-k,C] then set P[j,i,A] = true
if any of P[1,n,x] is true (x is iterated over the set s, where s are all the indices for Rs) then
S is member of language
else
S is not member of language
, by storing parse tree nodes as elements of the array, instead of booleans. Since the grammars being recognized can be ambiguous, it is necessary to store a list of nodes (unless one wishes to only pick one possible parse tree); the end result is then a forest of possible parse trees.
An alternative formulation employs a second table B[n,n,r] of so-called backpointers.
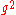to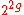 
, depending on the transformation algorithm used. For the use in teaching, they propose a slight generalization of the CYK algorithm, "without compromising efficiency of the algorithm, clarity of its presentation, or simplicity of proofs" .
and stochastic context-free grammar
s. Weights (probabilities) are then stored in the table P instead of booleans, so P[i,j,A] will contain the minimum weight (maximum probability) that the substring from i to j can be derived from A. Further extensions of the algorithm allow all parses of a string to be enumerated from lowest to highest weight (highest to lowest probability).
of CYK is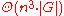
, where n is the length of the parsed string and |G| is the size of the CNF grammar G. This makes it one of the most efficient algorithms for recognizing general context-free languages in practice. gave an extension of the CYK algorithm. His algorithm computes the same parsing table
as the CYK algorithm; yet he showed that algorithms for efficient multiplication of matrices with 0-1-entries can be utilized for performing this computation.
Using the Coppersmith–Winograd algorithm
for multiplying these matrices, this gives an asymptotic worst-case running time of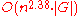
. However, the constant term hidden by the Big O Notation
is so large that the Coppersmith–Winograd algorithm is only worthwhile for matrices that are too large to handle on present-day computers . The dependence on efficient matrix multiplication cannot be avoided altogether: has proved that any parser for context-free grammars working in time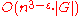
can be effectively converted into an algorithm computing the product of 
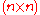-matrices with 0-1-entries in time 
.
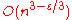Parsing
In computer science and linguistics, parsing, or, more formally, syntactic analysis, is the process of analyzing a text, made of a sequence of tokens , to determine its grammatical structure with respect to a given formal grammar...
algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for context-free grammar
Context-free grammar
In formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....
s. It employs bottom-up parsing
Bottom-up parsing
Bottom-up parsing is a strategy for analyzing unknown information that attempts to identify the most fundamental units first, and then to infer higher-order structures from them...
and dynamic programming
Dynamic programming
In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...
.
The standard version of CYK operates only on context-free grammars given in Chomsky normal form
Chomsky normal form
In computer science, a context-free grammar is said to be in Chomsky normal form if all of its production rules are of the form:Every grammar in Chomsky normal form is context-free, and conversely, every context-free grammar can be transformed into an equivalent one which is in Chomsky normal form....
(CNF). However any context-free grammar may be transformed to a CNF grammar expressing the same language .
The importance of the CYK algorithm stems from its high efficiency in certain situations. Using Landau symbols, the worst case running time
Analysis of algorithms
To analyze an algorithm is to determine the amount of resources necessary to execute it. Most algorithms are designed to work with inputs of arbitrary length...
of CYK is
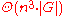, where n is the length of the parsed string and |G| is the size of the CNF grammar G. This makes it the most efficient parsing algorithm in terms of worst-case asymptotic complexity, although other algorithms exist with better average running time in many practical scenarios.Standard form
The algorithm requires the context-free grammar to be rendered into Chomsky normal formChomsky normal form
In computer science, a context-free grammar is said to be in Chomsky normal form if all of its production rules are of the form:Every grammar in Chomsky normal form is context-free, and conversely, every context-free grammar can be transformed into an equivalent one which is in Chomsky normal form....
(CNF), because it tests for possibilities to split the current sequence in half. Any context-free grammar can be represented in CNF using only rules of the forms
and .As pseudocode
The algorithm in pseudocodePseudocode
In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
is as follows:
let the input be a string S consisting of n characters: a1 ... an.
let the grammar contain r nonterminal symbols R1 ... Rr.
This grammar contains the subset Rs which is the set of start symbols.
let P[n,n,r] be an array of booleans. Initialize all elements of P to false.
for each i = 1 to n
for each unit production Rj -> ai
set P[i,1,j] = true
for each i = 2 to n -- Length of span
for each j = 1 to n-i+1 -- Start of span
for each k = 1 to i-1 -- Partition of span
for each production RA -> RB RC
if P[j,k,B] and P[j+k,i-k,C] then set P[j,i,A] = true
if any of P[1,n,x] is true (x is iterated over the set s, where s are all the indices for Rs) then
S is member of language
else
S is not member of language
As prose
In informal terms, this algorithm considers every possible subsequence of the sequence of words and sets P[i,j,k] to be true if the subsequence of words starting from i of length j can be generated from Rk. Once it has considered subsequences of length 1, it goes on to subsequences of length 2, and so on. For subsequences of length 2 and greater, it considers every possible partition of the subsequence into two parts, and checks to see if there is some production P → Q R such that Q matches the first part and R matches the second part. If so, it records P as matching the whole subsequence. Once this process is completed, the sentence is recognized by the grammar if the subsequence containing the entire sentence is matched by the start symbol.| S | ||||||
| VP | ||||||
| S | ||||||
| VP | PP | |||||
| S | NP | NP | ||||
| NP | V, VP | Det. | N | P | Det | N |
| she | eats | a | fish | with | a | fork |
Generating a parse tree
It is simple to extend the above algorithm to not only determine if a sentence is in a language, but to also construct a parse treeParse tree
A concrete syntax tree or parse tree or parsing treeis an ordered, rooted tree that represents the syntactic structure of a string according to some formal grammar. In a parse tree, the interior nodes are labeled by non-terminals of the grammar, while the leaf nodes are labeled by terminals of the...
, by storing parse tree nodes as elements of the array, instead of booleans. Since the grammars being recognized can be ambiguous, it is necessary to store a list of nodes (unless one wishes to only pick one possible parse tree); the end result is then a forest of possible parse trees.
An alternative formulation employs a second table B[n,n,r] of so-called backpointers.
Parsing non-CNF context-free grammars
As pointed out by , the drawback of all known transformations into Chomsky normal form is that they can lead to an undesirable bloat in grammar size. Using g to denote the size of the original grammar, the size blow-up in the worst case may range from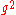 to 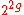, depending on the transformation algorithm used. For the use in teaching, they propose a slight generalization of the CYK algorithm, "without compromising efficiency of the algorithm, clarity of its presentation, or simplicity of proofs" .Parsing weighted context-free grammars
It is also possible to extend the CYK algorithm to parse strings using weightedWeighted context-free grammar
A weighted context-free grammar is a context-free grammar where each production has a numeric weight associated with it. The weight of a parse tree in a WCFG is the weight of the rule used to produce the top node, plus the weights of its children...
and stochastic context-free grammar
Stochastic context-free grammar
A stochastic context-free grammar is a context-free grammar in which each production is augmented with a probability...
s. Weights (probabilities) are then stored in the table P instead of booleans, so P[i,j,A] will contain the minimum weight (maximum probability) that the substring from i to j can be derived from A. Further extensions of the algorithm allow all parses of a string to be enumerated from lowest to highest weight (highest to lowest probability).
Valiant's algorithm
The worst case running timeAnalysis of algorithms
To analyze an algorithm is to determine the amount of resources necessary to execute it. Most algorithms are designed to work with inputs of arbitrary length...
of CYK is
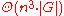, where n is the length of the parsed string and |G| is the size of the CNF grammar G. This makes it one of the most efficient algorithms for recognizing general context-free languages in practice. gave an extension of the CYK algorithm. His algorithm computes the same parsing tableas the CYK algorithm; yet he showed that algorithms for efficient multiplication of matrices with 0-1-entries can be utilized for performing this computation.
Using the Coppersmith–Winograd algorithm
Coppersmith–Winograd algorithm
In the mathematical discipline of linear algebra, the Coppersmith–Winograd algorithm, named after Don Coppersmith and Shmuel Winograd, is the asymptotically fastest known algorithm for square matrix multiplication. It can multiply two n \times n matrices in O time...
for multiplying these matrices, this gives an asymptotic worst-case running time of
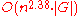. However, the constant term hidden by the Big O NotationBig O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
is so large that the Coppersmith–Winograd algorithm is only worthwhile for matrices that are too large to handle on present-day computers . The dependence on efficient matrix multiplication cannot be avoided altogether: has proved that any parser for context-free grammars working in time
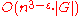can be effectively converted into an algorithm computing the product of 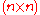-matrices with 0-1-entries in time .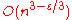