Coppersmith–Winograd algorithm
Encyclopedia
In the mathematical
discipline of linear algebra
, the Coppersmith–Winograd algorithm, named after Don Coppersmith
and Shmuel Winograd
, is the asymptotically fastest known algorithm
for square matrix multiplication
. It can multiply two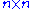
matrices in 
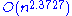time (see Big O notation
). This is an improvement over the trivial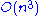
time algorithm and the 
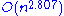time Strassen algorithm
. It is possible to improve the exponent further; however, the exponent must be at least 2 (because an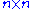
matrix has 
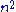values, and all of them have to be read at least once to calculate the exact result). It was known that the complexity of this algorithm is 
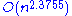. In 2010, however, Stothers gave a tighter analysis of the algorithm, 
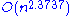. Williams improved the bound to 
.
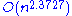The Coppersmith–Winograd algorithm is frequently used as a building block in other algorithms to prove theoretical time bounds. However, unlike the Strassen algorithm, it is not used in practice because it only provides an advantage for matrices so large that they cannot be processed by modern hardware.
Henry Cohn, Robert Kleinberg, Balázs Szegedy and Christopher Umans have rederived the Coppersmith–Winograd algorithm using a group-theoretic
construction. They also show that either of two different conjectures would imply that the optimal exponent of matrix multiplication is 2, as has long been suspected.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
discipline of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the Coppersmith–Winograd algorithm, named after Don Coppersmith
Don Coppersmith
Don Coppersmith is a cryptographer and mathematician. He was involved in the design of the Data Encryption Standard block cipher at IBM, particularly the design of the S-boxes, strengthening them against differential cryptanalysis...
and Shmuel Winograd
Shmuel Winograd
Shmuel Winograd is an American computer scientist, noted for his contributions to computational complexity. He has proved several major results regarding the computational aspects of arithmetic; his contributions include the Coppersmith-Winograd algorithm and an algorithm for Fast Fourier...
, is the asymptotically fastest known algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for square matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. It can multiply two
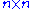matrices in 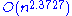time (see Big O notationBig O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
). This is an improvement over the trivial
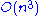time algorithm and the 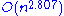time Strassen algorithmStrassen algorithm
In the mathematical discipline of linear algebra, the Strassen algorithm, named after Volker Strassen, is an algorithm used for matrix multiplication...
. It is possible to improve the exponent further; however, the exponent must be at least 2 (because an
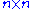matrix has 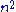values, and all of them have to be read at least once to calculate the exact result). It was known that the complexity of this algorithm is 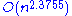. In 2010, however, Stothers gave a tighter analysis of the algorithm, 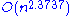. Williams improved the bound to 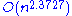.The Coppersmith–Winograd algorithm is frequently used as a building block in other algorithms to prove theoretical time bounds. However, unlike the Strassen algorithm, it is not used in practice because it only provides an advantage for matrices so large that they cannot be processed by modern hardware.
Henry Cohn, Robert Kleinberg, Balázs Szegedy and Christopher Umans have rederived the Coppersmith–Winograd algorithm using a group-theoretic
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
construction. They also show that either of two different conjectures would imply that the optimal exponent of matrix multiplication is 2, as has long been suspected.