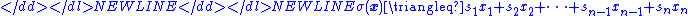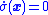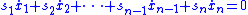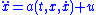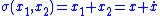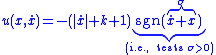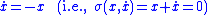Sliding mode control
Encyclopedia
In control theory
, sliding mode control, or SMC, is a nonlinear control
method that alters the dynamics of a nonlinear system by application of a discontinuous control signal that forces the system to "slide" along a cross-section of the system's normal behavior. The state
-feedback
control law is not a continuous function
of time. Instead, it can switch from one continuous structure to another based on the current position in the state space. Hence, sliding mode control is a variable structure control
method. The multiple control structures are designed so that trajectories always move toward an adjacent region with a different control structure, and so the ultimate trajectory will not exist entirely within one control structure. Instead, it will slide along the boundaries of the control structures. The motion of the system as it slides along these boundaries is called a sliding mode and the geometrical locus
consisting of the boundaries is called the sliding (hyper)surface. In the context of modern control theory, any variable structure system, like a system under SMC, may be viewed as a special case of a hybrid dynamical system
as the system both flows through a continuous state space but also moves through different discrete control modes.
Figure 1 shows an example trajectory of a system under sliding mode control. The sliding surface is described by , and the sliding mode along the surface commences after the finite time when system trajectories have reached the surface. In the theoretical description of sliding modes, the system stays confined to the sliding surface and need only be viewed as sliding along the surface. However, real implementations of sliding mode control approximate this theoretical behavior with a high-frequency and generally non-deterministic switching control signal that causes the system to "chatter" in a tight neighborhood of the sliding surface. This chattering behavior is evident in Figure 1, which chatters along the
, and the sliding mode along the surface commences after the finite time when system trajectories have reached the surface. In the theoretical description of sliding modes, the system stays confined to the sliding surface and need only be viewed as sliding along the surface. However, real implementations of sliding mode control approximate this theoretical behavior with a high-frequency and generally non-deterministic switching control signal that causes the system to "chatter" in a tight neighborhood of the sliding surface. This chattering behavior is evident in Figure 1, which chatters along the  surface as the system asymptotically approaches the origin, which is an asymptotically stable equilibrium of the system when confined to the sliding surface. In fact, although the system is nonlinear in general, the idealized (i.e., non-chattering) behavior of the system in Figure 1 when confined to the
surface as the system asymptotically approaches the origin, which is an asymptotically stable equilibrium of the system when confined to the sliding surface. In fact, although the system is nonlinear in general, the idealized (i.e., non-chattering) behavior of the system in Figure 1 when confined to the  surface is an LTI system with an exponentially stable origin.
surface is an LTI system with an exponentially stable origin.
Intuitively, sliding mode control uses practically infinite gain
to force the trajectories of a dynamic system to slide along the restricted sliding mode subspace. Trajectories from this reduced-order sliding mode have desirable properties (e.g., the system naturally slides along it until it comes to rest at a desired equilibrium
). The main strength of sliding mode control is its robustness
. Because the control can be as simple as a switching between two states (e.g., "on"/"off" or "forward"/"reverse"), it need not be precise and will not be sensitive to parameter variations that enter into the control channel. Additionally, because the control law is not a continuous function
, the sliding mode can be reached in finite time (i.e., better than asymptotic behavior). Under certain common conditions, optimality
requires the use of bang–bang control; hence, sliding mode control describes the optimal control
ler for a broad set of dynamic systems.
One application of sliding mode controllers is the control of electric drives operated by switching power converters. Because of the discontinuous operating mode of those converters, a discontinuous sliding mode controller is a natural implementation choice over continuous controllers that may need to be applied by means of pulse-width modulation
or a similar techniqueOther pulse-type modulation techniques include delta-sigma modulation
. of applying a continuous signal to an output that can only take discrete states.
Sliding mode control must be applied with more care than other forms of nonlinear control
that have more moderate control action. In particular, because actuators have delays and other imperfections, the hard sliding-mode-control action can lead to chatter, energy loss, plant damage, and excitation of unmodeled dynamics. Continuous control design methods are not as susceptible to these problems and can be made to mimic sliding-mode controllers.
where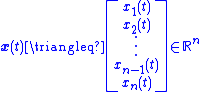
is an -dimensional state
-dimensional state
vector and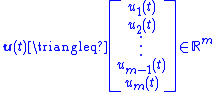
is an -dimensional input vector that will be used for state feedback
-dimensional input vector that will be used for state feedback
. The function
s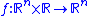 and
and 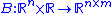 are assumed to be continuous
are assumed to be continuous
and sufficiently smooth
so that the Picard–Lindelöf theorem
can be used to guarantee that solution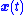 to Equation (1) exists
to Equation (1) exists
and is unique.
A common task is to design a state-feedback control law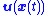 (i.e., a mapping from current state
(i.e., a mapping from current state 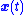 at time
at time  to the input
to the input  ) to stabilize
) to stabilize
the dynamical system
in Equation (1) around the origin
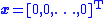 . That is, under the control law, whenever the system is started away from the origin, it will return to it. For example, the component
. That is, under the control law, whenever the system is started away from the origin, it will return to it. For example, the component 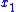 of the state vector
of the state vector  may represent the difference some output is away from a known signal (e.g., a desirable sinusoidal signal); if the control
may represent the difference some output is away from a known signal (e.g., a desirable sinusoidal signal); if the control  can ensure that
can ensure that 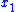 quickly returns to
quickly returns to  , then the output will track the desired sinusoid. In sliding-mode control, the designer knows that the system behaves desirably (e.g., it has a stable equilibrium
, then the output will track the desired sinusoid. In sliding-mode control, the designer knows that the system behaves desirably (e.g., it has a stable equilibrium
) provided that it is constrained to a subspace of its configuration space
. Sliding mode control forces the system trajectories into this subspace and then holds them there so that they slide along it. This reduced-order subspace is referred to as a sliding (hyper)surface, and when closed-loop feedback forces trajectories to slide along it, it is referred to as a sliding mode of the closed-loop system. Trajectories along this subspace can be likened to trajectories along eigenvectors (i.e., modes) of LTI systems; however, the sliding mode is enforced by creasing the vector field with high-gain feedback. Like a marble rolling along a crack, trajectories are confined to the sliding mode.
The sliding-mode control scheme involves
Because sliding mode control laws are not continuous
, it has the ability to drive trajectories to the sliding mode in finite time (i.e., stability of the sliding surface is better than asymptotic). However, once the trajectories reach the sliding surface, the system takes on the character of the sliding mode (e.g., the origin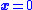 may only have asymptotic stability on this surface).
may only have asymptotic stability on this surface).
The sliding-mode designer picks a switching function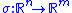 that represents a kind of "distance" that the states
that represents a kind of "distance" that the states  are away from a sliding surface.
are away from a sliding surface.
The sliding-mode-control law switches from one state to another based on the sign of this distance. So the sliding-mode control acts like a stiff pressure always pushing in the direction of the sliding mode where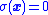 .
.
Desirable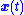 trajectories will approach the sliding surface, and because the control law is not continuous
trajectories will approach the sliding surface, and because the control law is not continuous
(i.e., it switches from one state to another as trajectories move across this surface), the surface is reached in finite time. Once a trajectory reaches the surface, it will slide along it and may, for example, move toward the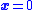 origin. So the switching function is like a topographic map
origin. So the switching function is like a topographic map
with a contour of constant height along which trajectories are forced to move.
The sliding (hyper)surface is of dimension where
where  is the number of states in
is the number of states in  and
and  is the number of input signals (i.e., control signals) in
is the number of input signals (i.e., control signals) in  . For each control index
. For each control index 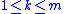 , there is an
, there is an 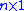 sliding surface given by
sliding surface given by
The vital part of VSC design is to choose a control law so that the sliding mode (i.e., this surface given by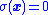 ) exists and is reachable along system trajectories. The principle of sliding mode control is to forcibly constrain the system, by suitable control strategy, to stay on the sliding surface on which the system will exhibit desirable features. When the system is constrained by the sliding control to stay on the sliding surface, the system dynamics are governed by reduced-order system obtained from Equation (2).
) exists and is reachable along system trajectories. The principle of sliding mode control is to forcibly constrain the system, by suitable control strategy, to stay on the sliding surface on which the system will exhibit desirable features. When the system is constrained by the sliding control to stay on the sliding surface, the system dynamics are governed by reduced-order system obtained from Equation (2).
To force the system states to satisfy
to satisfy 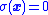 , one must:
, one must:
, it is certainly not locally Lipschitz continuous, and so existence and uniqueness of solutions to the closed-loop system is not guaranteed by the Picard–Lindelöf theorem
. Thus the solutions are to be understood in the Filippov sense. Roughly speaking, the resulting closed-loop system moving along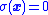 is approximated by the smooth dynamics
is approximated by the smooth dynamics 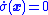 ; however, this smooth behavior may not be truly realizable. Similarly, high-speed pulse-width modulation
; however, this smooth behavior may not be truly realizable. Similarly, high-speed pulse-width modulation
or delta-sigma modulation
produces outputs that only assume two states, but the effective output swings through a continuous range of motion. These complications can be avoided by using a different nonlinear control
design method that produces a continuous controller. In some cases, sliding-mode control designs can be approximated by other continuous control designs.
candidate
where is the Euclidean norm (i.e.,
is the Euclidean norm (i.e., 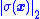 is the distance away from the sliding manifold where
is the distance away from the sliding manifold where  ). For the system given by Equation (1) and the sliding surface given by Equation (2), a sufficient condition for the existence of a sliding mode is that
). For the system given by Equation (1) and the sliding surface given by Equation (2), a sufficient condition for the existence of a sliding mode is that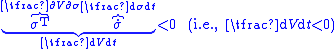
in a neighborhood
of the surface given by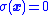 .
.
Roughly speaking (i.e., for the scalar
control case when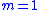 ), to achieve
), to achieve 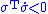 , the feedback control law
, the feedback control law 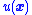 is picked so that
is picked so that  and
and 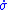 have opposite signs. That is,
have opposite signs. That is,
Note that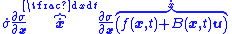
and so the feedback control law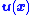 has a direct impact on
has a direct impact on 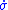 .
.
 is attained in finite time,
is attained in finite time, 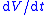 must be more strongly bounded away from zero. That is, if it vanishes too quickly, the attraction to the sliding mode will only be asymptotic. To ensure that the sliding mode is entered in finite time,
must be more strongly bounded away from zero. That is, if it vanishes too quickly, the attraction to the sliding mode will only be asymptotic. To ensure that the sliding mode is entered in finite time,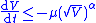
where and
and 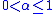 are constants.
are constants.
Explanation by comparison lemma
This condition ensures that for the neighborhood of the sliding mode ,
,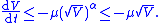
So, for ,
,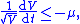
which, by the chain rule
(i.e.,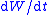 with
with  ), means
), means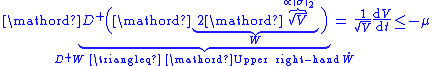
where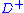 is the upper right-hand derivative of
is the upper right-hand derivative of  and the symbol
and the symbol  denotes proportionality
denotes proportionality
. So, by comparison to the curve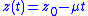 which is represented by differential equation
which is represented by differential equation 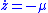 with initial condition
with initial condition 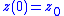 , it must be the case that
, it must be the case that 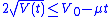 for all
for all  . Moreover, because
. Moreover, because 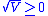 ,
,  must reach
must reach 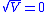 in finite time, which means that
in finite time, which means that  must reach
must reach 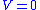 (i.e., the system enters the sliding mode) in finite time. Because
(i.e., the system enters the sliding mode) in finite time. Because 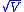 is proportional to the Euclidean norm
is proportional to the Euclidean norm  of the switching function
of the switching function  , this result implies that the rate of approach to the sliding mode must be firmly bounded away from zero.
, this result implies that the rate of approach to the sliding mode must be firmly bounded away from zero.
Consequences for sliding mode control
In the context of sliding mode control, this condition means that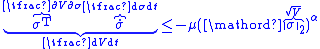
where is the Euclidean norm. For the case when switching function
is the Euclidean norm. For the case when switching function  is scalar valued, the sufficient condition becomes
is scalar valued, the sufficient condition becomes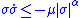 .
.
Taking , the scalar sufficient condition becomes
, the scalar sufficient condition becomes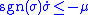
which is equivalent to the condition that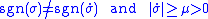 .
.
That is, the system should always be moving toward the switching surface , and its speed
, and its speed  toward the switching surface should have a non-zero lower bound. So, even though
toward the switching surface should have a non-zero lower bound. So, even though  may become vanishingly small as
may become vanishingly small as  approaches the
approaches the 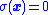 surface,
surface, 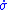 must always be bounded firmly away from zero. To ensure this condition, sliding mode controllers are discontinuous across the
must always be bounded firmly away from zero. To ensure this condition, sliding mode controllers are discontinuous across the  manifold; they switch from one non-zero value to another as trajectories cross the manifold.
manifold; they switch from one non-zero value to another as trajectories cross the manifold.
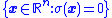 surface is reachable is given by
surface is reachable is given by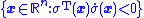
That is, when initial conditions come entirely from this space, the Lyapunov function candidate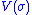 is a Lyapunov function
is a Lyapunov function
and trajectories are sure to move toward the sliding mode surface where
trajectories are sure to move toward the sliding mode surface where 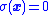 . Moreover, if the reachability conditions from Theorem 1 are satisfied, the sliding mode will enter the region where
. Moreover, if the reachability conditions from Theorem 1 are satisfied, the sliding mode will enter the region where  is more strongly bounded away from zero in finite time. Hence, the sliding mode
is more strongly bounded away from zero in finite time. Hence, the sliding mode  will be attained in finite time.
will be attained in finite time.
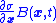
be nonsingular. That is, the system has a kind of controllability
that ensures that there is always a control that can move a trajectory to move closer to the sliding mode. Then, once the sliding mode where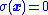 is achieved, the system will stay on that sliding mode. Along sliding mode trajectories,
is achieved, the system will stay on that sliding mode. Along sliding mode trajectories, 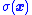 is constant, and so sliding mode trajectories are described by the differential equation
is constant, and so sliding mode trajectories are described by the differential equation .
.
If an -equilibrium
-equilibrium
is stable
with respect to this differential equation, then the system will slide along the sliding mode surface toward the equilibrium.
The equivalent control law on the sliding mode can be found by solving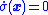
for the equivalent control law . That is,
. That is,
and so the equivalent control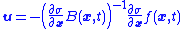
That is, even though the actual control is not continuous
is not continuous
, the rapid switching across the sliding mode where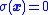 forces the system to act as if it were driven by this continuous control.
forces the system to act as if it were driven by this continuous control.
Likewise, the system trajectories on the sliding mode behave as if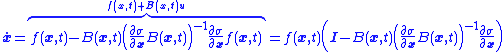
The resulting system matches the sliding mode differential equation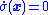
and so as long as the sliding mode surface where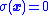 is stable (in the sense of Lyapunov), the system can be assumed to follow the simpler
is stable (in the sense of Lyapunov), the system can be assumed to follow the simpler  condition after some initial transient during the period while the system finds the sliding mode. The same motion is approximately maintained provided the equality
condition after some initial transient during the period while the system finds the sliding mode. The same motion is approximately maintained provided the equality 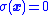 only approximately holds.
only approximately holds.
It follows from these theorems that the sliding motion is invariant (i.e., insensitive) to sufficiently small disturbances entering the system through the control channel. That is, as long as the control is large enough to ensure that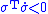 and
and 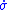 is uniformly bounded away from zero, the sliding mode will be maintained as if there was no disturbance. The invariance property of sliding mode control to certain disturbances and model uncertainties is its most attractive feature; it is strongly robust
is uniformly bounded away from zero, the sliding mode will be maintained as if there was no disturbance. The invariance property of sliding mode control to certain disturbances and model uncertainties is its most attractive feature; it is strongly robust
.
As discussed in an example below, a sliding mode control law can keep the constraint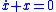
in order to asymptotically stabilize any system of the form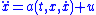
when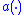 has a finite upper bound. In this case, the sliding mode is where
has a finite upper bound. In this case, the sliding mode is where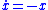
(i.e., where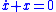 ). That is, when the system is constrained this way, it behaves like a simple stable
). That is, when the system is constrained this way, it behaves like a simple stable
linear system
, and so it has a globally exponentially stable equilibrium at the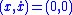 origin.
origin.
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, sliding mode control, or SMC, is a nonlinear control
Nonlinear control
Nonlinear control is the area of control engineering specifically involved with systems that are nonlinear, time-variant, or both. Many well-established analysis and design techniques exist for LTI systems ; however, one or both of the controller and the system under control in a general control...
method that alters the dynamics of a nonlinear system by application of a discontinuous control signal that forces the system to "slide" along a cross-section of the system's normal behavior. The state
State space (controls)
In control engineering, a state space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations...
-feedback
Feedback
Feedback describes the situation when output from an event or phenomenon in the past will influence an occurrence or occurrences of the same Feedback describes the situation when output from (or information about the result of) an event or phenomenon in the past will influence an occurrence or...
control law is not a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
of time. Instead, it can switch from one continuous structure to another based on the current position in the state space. Hence, sliding mode control is a variable structure control
Variable structure control
Variable structure control, or VSC, is a form of discontinuous nonlinear control. The method alters the dynamics of a nonlinear system by application of a high-frequency switching control. The state-feedback control law is not a continuous function of time; it switches from one smooth condition to...
method. The multiple control structures are designed so that trajectories always move toward an adjacent region with a different control structure, and so the ultimate trajectory will not exist entirely within one control structure. Instead, it will slide along the boundaries of the control structures. The motion of the system as it slides along these boundaries is called a sliding mode and the geometrical locus
Locus (mathematics)
In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
consisting of the boundaries is called the sliding (hyper)surface. In the context of modern control theory, any variable structure system, like a system under SMC, may be viewed as a special case of a hybrid dynamical system
Hybrid system
A hybrid system is a dynamic system that exhibits both continuous and discrete dynamic behavior – a system that can both flow and jump...
as the system both flows through a continuous state space but also moves through different discrete control modes.
Figure 1 shows an example trajectory of a system under sliding mode control. The sliding surface is described by
 , and the sliding mode along the surface commences after the finite time when system trajectories have reached the surface. In the theoretical description of sliding modes, the system stays confined to the sliding surface and need only be viewed as sliding along the surface. However, real implementations of sliding mode control approximate this theoretical behavior with a high-frequency and generally non-deterministic switching control signal that causes the system to "chatter" in a tight neighborhood of the sliding surface. This chattering behavior is evident in Figure 1, which chatters along the
, and the sliding mode along the surface commences after the finite time when system trajectories have reached the surface. In the theoretical description of sliding modes, the system stays confined to the sliding surface and need only be viewed as sliding along the surface. However, real implementations of sliding mode control approximate this theoretical behavior with a high-frequency and generally non-deterministic switching control signal that causes the system to "chatter" in a tight neighborhood of the sliding surface. This chattering behavior is evident in Figure 1, which chatters along the  surface as the system asymptotically approaches the origin, which is an asymptotically stable equilibrium of the system when confined to the sliding surface. In fact, although the system is nonlinear in general, the idealized (i.e., non-chattering) behavior of the system in Figure 1 when confined to the
surface as the system asymptotically approaches the origin, which is an asymptotically stable equilibrium of the system when confined to the sliding surface. In fact, although the system is nonlinear in general, the idealized (i.e., non-chattering) behavior of the system in Figure 1 when confined to the  surface is an LTI system with an exponentially stable origin.
surface is an LTI system with an exponentially stable origin.Intuitively, sliding mode control uses practically infinite gain
Gain
In electronics, gain is a measure of the ability of a circuit to increase the power or amplitude of a signal from the input to the output. It is usually defined as the mean ratio of the signal output of a system to the signal input of the same system. It may also be defined on a logarithmic scale,...
to force the trajectories of a dynamic system to slide along the restricted sliding mode subspace. Trajectories from this reduced-order sliding mode have desirable properties (e.g., the system naturally slides along it until it comes to rest at a desired equilibrium
Stationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
). The main strength of sliding mode control is its robustness
Robust control
Robust control is a branch of control theory that explicitly deals with uncertainty in its approach to controller design. Robust control methods are designed to function properly so long as uncertain parameters or disturbances are within some set...
. Because the control can be as simple as a switching between two states (e.g., "on"/"off" or "forward"/"reverse"), it need not be precise and will not be sensitive to parameter variations that enter into the control channel. Additionally, because the control law is not a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, the sliding mode can be reached in finite time (i.e., better than asymptotic behavior). Under certain common conditions, optimality
Optimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
requires the use of bang–bang control; hence, sliding mode control describes the optimal control
Optimal control
Optimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
ler for a broad set of dynamic systems.
One application of sliding mode controllers is the control of electric drives operated by switching power converters. Because of the discontinuous operating mode of those converters, a discontinuous sliding mode controller is a natural implementation choice over continuous controllers that may need to be applied by means of pulse-width modulation
Pulse-width modulation
Pulse-width modulation , or pulse-duration modulation , is a commonly used technique for controlling power to inertial electrical devices, made practical by modern electronic power switches....
or a similar techniqueOther pulse-type modulation techniques include delta-sigma modulation
Delta-sigma modulation
Delta-sigma modulation is a method for encoding high-resolution or analog signals into lower-resolution digital signals. The conversion is done using error feedback, where the difference between the two signals is measured and used to improve the conversion...
. of applying a continuous signal to an output that can only take discrete states.
Sliding mode control must be applied with more care than other forms of nonlinear control
Nonlinear control
Nonlinear control is the area of control engineering specifically involved with systems that are nonlinear, time-variant, or both. Many well-established analysis and design techniques exist for LTI systems ; however, one or both of the controller and the system under control in a general control...
that have more moderate control action. In particular, because actuators have delays and other imperfections, the hard sliding-mode-control action can lead to chatter, energy loss, plant damage, and excitation of unmodeled dynamics. Continuous control design methods are not as susceptible to these problems and can be made to mimic sliding-mode controllers.
Control scheme
Consider a nonlinear dynamical system described by |
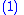 |
where
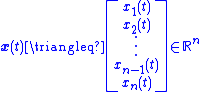
is an
 -dimensional state
-dimensional stateState space (controls)
In control engineering, a state space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations...
vector and
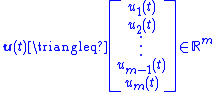
is an
 -dimensional input vector that will be used for state feedback
-dimensional input vector that will be used for state feedbackFeedback
Feedback describes the situation when output from an event or phenomenon in the past will influence an occurrence or occurrences of the same Feedback describes the situation when output from (or information about the result of) an event or phenomenon in the past will influence an occurrence or...
. The function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s
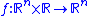 and
and 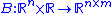 are assumed to be continuous
are assumed to be continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
and sufficiently smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
so that the Picard–Lindelöf theorem
Picard–Lindelöf theorem
In mathematics, in the study of differential equations, the Picard–Lindelöf theorem, Picard's existence theorem or Cauchy–Lipschitz theorem is an important theorem on existence and uniqueness of solutions to first-order equations with given initial conditions.The theorem is named after Charles...
can be used to guarantee that solution
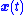 to Equation (1) exists
to Equation (1) existsExistence
In common usage, existence is the world we are aware of through our senses, and that persists independently without them. In academic philosophy the word has a more specialized meaning, being contrasted with essence, which specifies different forms of existence as well as different identity...
and is unique.
A common task is to design a state-feedback control law
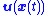 (i.e., a mapping from current state
(i.e., a mapping from current state 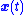 at time
at time  to the input
to the input  ) to stabilize
) to stabilizeLyapunov stability
Various types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
the dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
in Equation (1) around the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
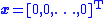 . That is, under the control law, whenever the system is started away from the origin, it will return to it. For example, the component
. That is, under the control law, whenever the system is started away from the origin, it will return to it. For example, the component 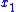 of the state vector
of the state vector  may represent the difference some output is away from a known signal (e.g., a desirable sinusoidal signal); if the control
may represent the difference some output is away from a known signal (e.g., a desirable sinusoidal signal); if the control  can ensure that
can ensure that 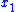 quickly returns to
quickly returns to  , then the output will track the desired sinusoid. In sliding-mode control, the designer knows that the system behaves desirably (e.g., it has a stable equilibrium
, then the output will track the desired sinusoid. In sliding-mode control, the designer knows that the system behaves desirably (e.g., it has a stable equilibriumStationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
) provided that it is constrained to a subspace of its configuration space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
. Sliding mode control forces the system trajectories into this subspace and then holds them there so that they slide along it. This reduced-order subspace is referred to as a sliding (hyper)surface, and when closed-loop feedback forces trajectories to slide along it, it is referred to as a sliding mode of the closed-loop system. Trajectories along this subspace can be likened to trajectories along eigenvectors (i.e., modes) of LTI systems; however, the sliding mode is enforced by creasing the vector field with high-gain feedback. Like a marble rolling along a crack, trajectories are confined to the sliding mode.
The sliding-mode control scheme involves
- Selection of a hypersurfaceHypersurfaceIn geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
or a manifold (i.e., the sliding surface) such that the system trajectory exhibits desirable behavior when confined to this manifold. - Finding feedback gains so that the system trajectory intersects and stays on the manifold.
Because sliding mode control laws are not continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, it has the ability to drive trajectories to the sliding mode in finite time (i.e., stability of the sliding surface is better than asymptotic). However, once the trajectories reach the sliding surface, the system takes on the character of the sliding mode (e.g., the origin
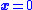 may only have asymptotic stability on this surface).
may only have asymptotic stability on this surface).The sliding-mode designer picks a switching function
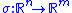 that represents a kind of "distance" that the states
that represents a kind of "distance" that the states  are away from a sliding surface.
are away from a sliding surface.
- A state
 that is outside of this sliding surface has
that is outside of this sliding surface has 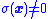 .
. - A state that is on this sliding surface has
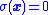 .
.
The sliding-mode-control law switches from one state to another based on the sign of this distance. So the sliding-mode control acts like a stiff pressure always pushing in the direction of the sliding mode where
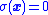 .
.Desirable
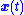 trajectories will approach the sliding surface, and because the control law is not continuous
trajectories will approach the sliding surface, and because the control law is not continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
(i.e., it switches from one state to another as trajectories move across this surface), the surface is reached in finite time. Once a trajectory reaches the surface, it will slide along it and may, for example, move toward the
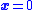 origin. So the switching function is like a topographic map
origin. So the switching function is like a topographic mapTopographic map
A topographic map is a type of map characterized by large-scale detail and quantitative representation of relief, usually using contour lines in modern mapping, but historically using a variety of methods. Traditional definitions require a topographic map to show both natural and man-made features...
with a contour of constant height along which trajectories are forced to move.
The sliding (hyper)surface is of dimension
 where
where  is the number of states in
is the number of states in  and
and  is the number of input signals (i.e., control signals) in
is the number of input signals (i.e., control signals) in  . For each control index
. For each control index 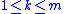 , there is an
, there is an 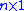 sliding surface given by
sliding surface given by
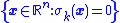 |
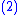 |
The vital part of VSC design is to choose a control law so that the sliding mode (i.e., this surface given by
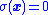 ) exists and is reachable along system trajectories. The principle of sliding mode control is to forcibly constrain the system, by suitable control strategy, to stay on the sliding surface on which the system will exhibit desirable features. When the system is constrained by the sliding control to stay on the sliding surface, the system dynamics are governed by reduced-order system obtained from Equation (2).
) exists and is reachable along system trajectories. The principle of sliding mode control is to forcibly constrain the system, by suitable control strategy, to stay on the sliding surface on which the system will exhibit desirable features. When the system is constrained by the sliding control to stay on the sliding surface, the system dynamics are governed by reduced-order system obtained from Equation (2).To force the system states
 to satisfy
to satisfy 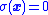 , one must:
, one must:
- Ensure that the system is capable of reaching
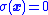 from any initial condition
from any initial condition - Having reached
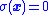 , the control action is capable of maintaining the system at
, the control action is capable of maintaining the system at 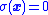
Existence of closed-loop solutions
Note that because the control law is not continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, it is certainly not locally Lipschitz continuous, and so existence and uniqueness of solutions to the closed-loop system is not guaranteed by the Picard–Lindelöf theorem
Picard–Lindelöf theorem
In mathematics, in the study of differential equations, the Picard–Lindelöf theorem, Picard's existence theorem or Cauchy–Lipschitz theorem is an important theorem on existence and uniqueness of solutions to first-order equations with given initial conditions.The theorem is named after Charles...
. Thus the solutions are to be understood in the Filippov sense. Roughly speaking, the resulting closed-loop system moving along
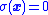 is approximated by the smooth dynamics
is approximated by the smooth dynamics 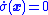 ; however, this smooth behavior may not be truly realizable. Similarly, high-speed pulse-width modulation
; however, this smooth behavior may not be truly realizable. Similarly, high-speed pulse-width modulationPulse-width modulation
Pulse-width modulation , or pulse-duration modulation , is a commonly used technique for controlling power to inertial electrical devices, made practical by modern electronic power switches....
or delta-sigma modulation
Delta-sigma modulation
Delta-sigma modulation is a method for encoding high-resolution or analog signals into lower-resolution digital signals. The conversion is done using error feedback, where the difference between the two signals is measured and used to improve the conversion...
produces outputs that only assume two states, but the effective output swings through a continuous range of motion. These complications can be avoided by using a different nonlinear control
Nonlinear control
Nonlinear control is the area of control engineering specifically involved with systems that are nonlinear, time-variant, or both. Many well-established analysis and design techniques exist for LTI systems ; however, one or both of the controller and the system under control in a general control...
design method that produces a continuous controller. In some cases, sliding-mode control designs can be approximated by other continuous control designs.
Theorem 1: Existence of Sliding Mode
Consider a Lyapunov functionLyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
candidate
 |
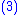 |
where
 is the Euclidean norm (i.e.,
is the Euclidean norm (i.e., 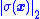 is the distance away from the sliding manifold where
is the distance away from the sliding manifold where  ). For the system given by Equation (1) and the sliding surface given by Equation (2), a sufficient condition for the existence of a sliding mode is that
). For the system given by Equation (1) and the sliding surface given by Equation (2), a sufficient condition for the existence of a sliding mode is that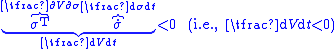
in a neighborhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
of the surface given by
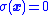 .
.Roughly speaking (i.e., for the scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
control case when
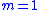 ), to achieve
), to achieve 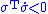 , the feedback control law
, the feedback control law 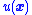 is picked so that
is picked so that  and
and 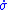 have opposite signs. That is,
have opposite signs. That is,
-
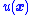 makes
makes 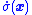 negative when
negative when 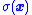 is positive.
is positive. -
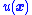 makes
makes 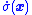 positive when
positive when 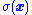 is negative.
is negative.
Note that
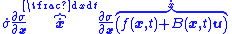
and so the feedback control law
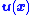 has a direct impact on
has a direct impact on 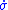 .
.Reachability: Attaining sliding manifold in finite time
To ensure that the sliding mode is attained in finite time,
is attained in finite time, 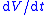 must be more strongly bounded away from zero. That is, if it vanishes too quickly, the attraction to the sliding mode will only be asymptotic. To ensure that the sliding mode is entered in finite time,
must be more strongly bounded away from zero. That is, if it vanishes too quickly, the attraction to the sliding mode will only be asymptotic. To ensure that the sliding mode is entered in finite time,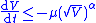
where
 and
and 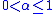 are constants.
are constants.Explanation by comparison lemma
This condition ensures that for the neighborhood of the sliding mode
 ,
,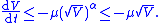
So, for
 ,
,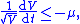
which, by the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
(i.e.,
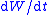 with
with  ), means
), means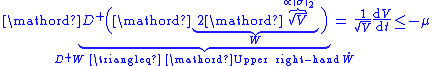
where
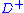 is the upper right-hand derivative of
is the upper right-hand derivative of  and the symbol
and the symbol  denotes proportionality
denotes proportionalityProportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
. So, by comparison to the curve
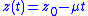 which is represented by differential equation
which is represented by differential equation 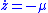 with initial condition
with initial condition 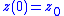 , it must be the case that
, it must be the case that 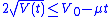 for all
for all  . Moreover, because
. Moreover, because 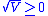 ,
,  must reach
must reach 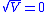 in finite time, which means that
in finite time, which means that  must reach
must reach 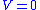 (i.e., the system enters the sliding mode) in finite time. Because
(i.e., the system enters the sliding mode) in finite time. Because 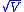 is proportional to the Euclidean norm
is proportional to the Euclidean norm  of the switching function
of the switching function  , this result implies that the rate of approach to the sliding mode must be firmly bounded away from zero.
, this result implies that the rate of approach to the sliding mode must be firmly bounded away from zero.Consequences for sliding mode control
In the context of sliding mode control, this condition means that
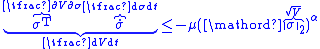
where
 is the Euclidean norm. For the case when switching function
is the Euclidean norm. For the case when switching function  is scalar valued, the sufficient condition becomes
is scalar valued, the sufficient condition becomes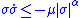 .
.Taking
 , the scalar sufficient condition becomes
, the scalar sufficient condition becomes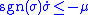
which is equivalent to the condition that
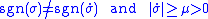 .
.That is, the system should always be moving toward the switching surface
 , and its speed
, and its speed  toward the switching surface should have a non-zero lower bound. So, even though
toward the switching surface should have a non-zero lower bound. So, even though  may become vanishingly small as
may become vanishingly small as  approaches the
approaches the 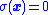 surface,
surface, 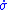 must always be bounded firmly away from zero. To ensure this condition, sliding mode controllers are discontinuous across the
must always be bounded firmly away from zero. To ensure this condition, sliding mode controllers are discontinuous across the  manifold; they switch from one non-zero value to another as trajectories cross the manifold.
manifold; they switch from one non-zero value to another as trajectories cross the manifold.Theorem 2: Region of Attraction
For the system given by Equation (1) and sliding surface given by Equation (2), the subspace for which the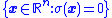 surface is reachable is given by
surface is reachable is given by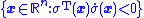
That is, when initial conditions come entirely from this space, the Lyapunov function candidate
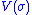 is a Lyapunov function
is a Lyapunov functionLyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
and
 trajectories are sure to move toward the sliding mode surface where
trajectories are sure to move toward the sliding mode surface where 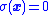 . Moreover, if the reachability conditions from Theorem 1 are satisfied, the sliding mode will enter the region where
. Moreover, if the reachability conditions from Theorem 1 are satisfied, the sliding mode will enter the region where  is more strongly bounded away from zero in finite time. Hence, the sliding mode
is more strongly bounded away from zero in finite time. Hence, the sliding mode  will be attained in finite time.
will be attained in finite time.Theorem 3: Sliding Motion
Let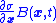
be nonsingular. That is, the system has a kind of controllability
Controllability
Controllability is an important property of a control system, and the controllability property plays a crucial role in many control problems, such as stabilization of unstable systems by feedback, or optimal control....
that ensures that there is always a control that can move a trajectory to move closer to the sliding mode. Then, once the sliding mode where
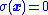 is achieved, the system will stay on that sliding mode. Along sliding mode trajectories,
is achieved, the system will stay on that sliding mode. Along sliding mode trajectories, 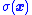 is constant, and so sliding mode trajectories are described by the differential equation
is constant, and so sliding mode trajectories are described by the differential equation .
.If an
 -equilibrium
-equilibriumStationary point
In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
is stable
Lyapunov stability
Various types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
with respect to this differential equation, then the system will slide along the sliding mode surface toward the equilibrium.
The equivalent control law on the sliding mode can be found by solving
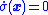
for the equivalent control law
 . That is,
. That is,
and so the equivalent control
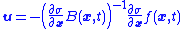
That is, even though the actual control
 is not continuous
is not continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, the rapid switching across the sliding mode where
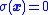 forces the system to act as if it were driven by this continuous control.
forces the system to act as if it were driven by this continuous control.Likewise, the system trajectories on the sliding mode behave as if
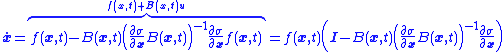
The resulting system matches the sliding mode differential equation
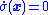
and so as long as the sliding mode surface where
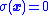 is stable (in the sense of Lyapunov), the system can be assumed to follow the simpler
is stable (in the sense of Lyapunov), the system can be assumed to follow the simpler  condition after some initial transient during the period while the system finds the sliding mode. The same motion is approximately maintained provided the equality
condition after some initial transient during the period while the system finds the sliding mode. The same motion is approximately maintained provided the equality 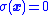 only approximately holds.
only approximately holds.It follows from these theorems that the sliding motion is invariant (i.e., insensitive) to sufficiently small disturbances entering the system through the control channel. That is, as long as the control is large enough to ensure that
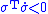 and
and 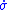 is uniformly bounded away from zero, the sliding mode will be maintained as if there was no disturbance. The invariance property of sliding mode control to certain disturbances and model uncertainties is its most attractive feature; it is strongly robust
is uniformly bounded away from zero, the sliding mode will be maintained as if there was no disturbance. The invariance property of sliding mode control to certain disturbances and model uncertainties is its most attractive feature; it is strongly robustRobust control
Robust control is a branch of control theory that explicitly deals with uncertainty in its approach to controller design. Robust control methods are designed to function properly so long as uncertain parameters or disturbances are within some set...
.
As discussed in an example below, a sliding mode control law can keep the constraint
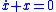
in order to asymptotically stabilize any system of the form
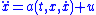
when
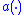 has a finite upper bound. In this case, the sliding mode is where
has a finite upper bound. In this case, the sliding mode is where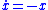
(i.e., where
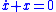 ). That is, when the system is constrained this way, it behaves like a simple stable
). That is, when the system is constrained this way, it behaves like a simple stableBIBO stability
In electrical engineering, specifically signal processing and control theory, BIBO stability is a form of stability for linear signals and systems that take inputs. BIBO stands for Bounded-Input Bounded-Output...
linear system
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
, and so it has a globally exponentially stable equilibrium at the
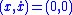 origin.
origin.Control design examples
- Consider a plantPlant (control theory)A plant in control theory is the combination of process and actuator....
described by Equation (1) with single input (i.e.,
(i.e., 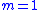 ). The switching function is picked to be the linear combination
). The switching function is picked to be the linear combination
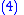
- where the weight
 for all
for all 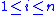 . The sliding surface is the simplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
. The sliding surface is the simplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
where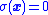 . When trajectories are forced to slide along this surface,
. When trajectories are forced to slide along this surface,
- and so
- which is a reduced-order system (i.e., the new system is of order
 because the system is constrained to this
because the system is constrained to this 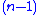 -dimensional sliding mode simplex). This surface may have favorable properties (e.g., when the plant dynamics are forced to slide along this surface, they move toward the origin
-dimensional sliding mode simplex). This surface may have favorable properties (e.g., when the plant dynamics are forced to slide along this surface, they move toward the origin 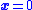 ). Taking the derivative of the Lyapunov functionLyapunov functionIn the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
). Taking the derivative of the Lyapunov functionLyapunov functionIn the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
in Equation (3), we have
- To ensure
 is a negative-definite function (i.e.,
is a negative-definite function (i.e., 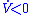 for Lyapunov stabilityLyapunov stabilityVarious types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
for Lyapunov stabilityLyapunov stabilityVarious types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
of the surface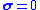 ), the feedback control law
), the feedback control law 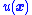 must be chosen so that
must be chosen so that
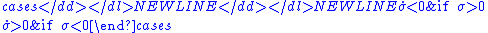
- Hence, the product
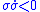 because it is the product of a negative and a positive number. Note that
because it is the product of a negative and a positive number. Note that
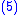
- The control law
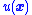 is chosen so that
is chosen so that
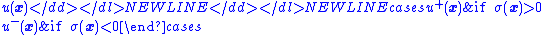
- where
-
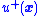 is some control (e.g., possibly extreme, like "on" or "forward") that ensures Equation (5) (i.e.,
is some control (e.g., possibly extreme, like "on" or "forward") that ensures Equation (5) (i.e., 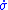 ) is negative at
) is negative at 
-
 is some control (e.g., possibly extreme, like "off" or "reverse") that ensures Equation (5) (i.e.,
is some control (e.g., possibly extreme, like "off" or "reverse") that ensures Equation (5) (i.e., 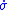 ) is positive at
) is positive at 
-
- The resulting trajectory should move toward the sliding surface where
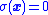 . Because real systems have delay, sliding mode trajectories often chatter back and forth along this sliding surface (i.e., the true trajectory may not smoothly follow
. Because real systems have delay, sliding mode trajectories often chatter back and forth along this sliding surface (i.e., the true trajectory may not smoothly follow 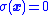 , but it will always return to the sliding mode after leaving it).
, but it will always return to the sliding mode after leaving it).
- Consider the dynamic system
-
- which can be expressed in a 2-dimensional state spaceState space (controls)In control engineering, a state space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations...
(with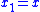 and
and  ) as
) as
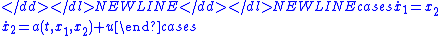
- Also assume that
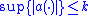 (i.e.,
(i.e.,  has a finite upper bound
has a finite upper bound  that is known). For this system, choose the switching function
that is known). For this system, choose the switching function
- By the previous example, we must choose the feedback control law
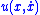 so that
so that  . Here,
. Here,
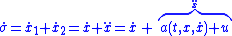
- When
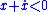 (i.e., when
(i.e., when  ), to make
), to make  , the control law should be picked so that
, the control law should be picked so that 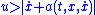
- When
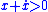 (i.e., when
(i.e., when  ), to make
), to make  , the control law should be picked so that
, the control law should be picked so that 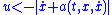
- When
- However, by the triangle inequalityTriangle inequalityIn mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
, - and by the assumption about
 ,
,
- So the system can be feedback stabilized (to return to the sliding mode) by means of the control law

- which can be expressed in closed formClosed-form expressionIn mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
as - Assuming that the system trajectories are forced to move so that
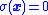 , then
, then
- So once the system reaches the sliding mode, the system's 2-dimensional dynamics behave like this 1-dimensional system, which has a globally exponentially stable equilibriumStationary pointIn mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
at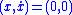 .
.
Sliding mode observer
Sliding mode control can be used in the design of state observerState observerIn control theory, a state observer is a system that models a real system in order to provide an estimate of its internal state, given measurements of the input and output of the real system. It is typically a computer-implemented mathematical model....
s. These non-linear high-gain observers have the ability to bring coordinates of the estimator error dynamics to zero in finite time. Additionally, switched-mode observers have attractive measurement noise resilience that is similar to a Kalman filterKalman filterIn statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
. For simplicity, the example here uses a traditional sliding mode modification of a Luenberger observer for an LTI system. In these sliding mode observers, the order of the observer dynamics are reduced by one when the system enters the sliding mode. In this particular example, the estimator error for a single estimated state is brought to zero in finite time, and after that time the other estimator errors decay exponentially to zero. However, as first described by Drakunov, a sliding mode observer for non-linear systems can be built that brings the estimation error for all estimated states to zero in a finite (and arbitrarily small) time.
Here, consider the LTI system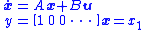
where state vector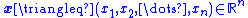 ,
, 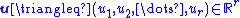 is a vector of inputs, and output
is a vector of inputs, and output  is a scalar equal to the first state of the
is a scalar equal to the first state of the  state vector. Let
state vector. Let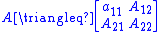
where-
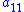 is a scalar representing the influence of the first state
is a scalar representing the influence of the first state 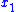 on itself,
on itself, -
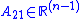 is a column vector representing the influence of the other states on the first state,
is a column vector representing the influence of the other states on the first state, -
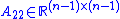 is a matrix representing the influence of the other states on themselves, and
is a matrix representing the influence of the other states on themselves, and -
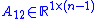 is a row vector corresponding to the influence of the first state on the other states.
is a row vector corresponding to the influence of the first state on the other states.
The goal is to design a high-gain state observer that estimates the state vector using only information from the measurement
using only information from the measurement 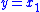 . Hence, let the vector
. Hence, let the vector 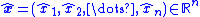 be the estimates of the
be the estimates of the  states. The observer takes the form
states. The observer takes the form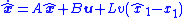
where is a nonlinear function of the error between estimated state
is a nonlinear function of the error between estimated state 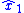 and the output
and the output 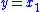 , and
, and 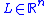 is an observer gain vector that serves a similar purpose as in the typical linear Luenberger observerState observerIn control theory, a state observer is a system that models a real system in order to provide an estimate of its internal state, given measurements of the input and output of the real system. It is typically a computer-implemented mathematical model....
is an observer gain vector that serves a similar purpose as in the typical linear Luenberger observerState observerIn control theory, a state observer is a system that models a real system in order to provide an estimate of its internal state, given measurements of the input and output of the real system. It is typically a computer-implemented mathematical model....
. Likewise, let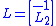
where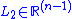 is a column vector. Additionally, let
is a column vector. Additionally, let 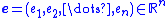 be the state estimator error. That is,
be the state estimator error. That is,  . The error dynamics are then
. The error dynamics are then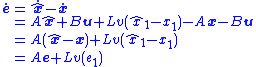
where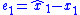 is the estimator error for the first state estimate. The nonlinear control law
is the estimator error for the first state estimate. The nonlinear control law  can be designed to enforce the sliding manifold
can be designed to enforce the sliding manifold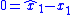
so that estimate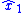 tracks the real state
tracks the real state 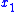 after some finite time (i.e.,
after some finite time (i.e.,  ). Hence, the sliding mode control switching function
). Hence, the sliding mode control switching function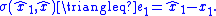
To attain the sliding manifold,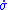 and
and  must always have opposite signs (i.e.,
must always have opposite signs (i.e., 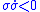 for essentiallyAlmost everywhereIn measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
for essentiallyAlmost everywhereIn measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
all ). However,
). However,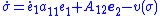
where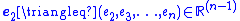 is the collection of the estimator errors for all of the unmeasured states. To ensure that
is the collection of the estimator errors for all of the unmeasured states. To ensure that 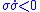 , let
, let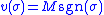
where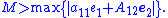
That is, positive constant must be greater that a scaled version of the maximum possible estimator errors for the system (i.e., the initial errors, which are assumed to be bounded so that
must be greater that a scaled version of the maximum possible estimator errors for the system (i.e., the initial errors, which are assumed to be bounded so that  can be picked large enough; al). If
can be picked large enough; al). If  is sufficiently large, it can be assumed that the system achieves
is sufficiently large, it can be assumed that the system achieves  (i.e.,
(i.e., 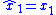 ). Because
). Because 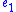 is constant (i.e., 0) along this manifold,
is constant (i.e., 0) along this manifold, 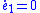 as well. Hence, the discontinuous control
as well. Hence, the discontinuous control 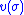 may be replaced with the equivalent continuous control
may be replaced with the equivalent continuous control 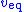 where
where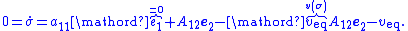
So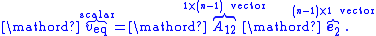
This equivalent control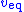 represents the contribution from the other
represents the contribution from the other  states to the trajectory of the output state
states to the trajectory of the output state 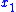 . In particular, the row
. In particular, the row 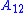 acts like an output vector for the error subsystem
acts like an output vector for the error subsystem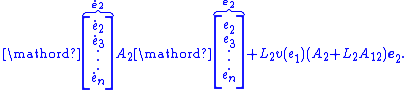
So, to ensure the estimator error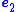 for the unmeasured states converges to zero, the
for the unmeasured states converges to zero, the  vector
vector  must be chosen so that the
must be chosen so that the  matrix
matrix 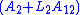 is HurwitzHurwitz matrix-Hurwitz matrix and the Hurwitz stability criterion:In mathematics, Hurwitz matrix is a structured real square matrix constructed with coefficientsof a real polynomial...
is HurwitzHurwitz matrix-Hurwitz matrix and the Hurwitz stability criterion:In mathematics, Hurwitz matrix is a structured real square matrix constructed with coefficientsof a real polynomial...
(i.e., the real part of each of its eigenvalues must be negative). Hence, provided that it is observableObservableIn physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
, this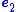 system can be stabilized in exactly the same way as a typical linear state observerState observerIn control theory, a state observer is a system that models a real system in order to provide an estimate of its internal state, given measurements of the input and output of the real system. It is typically a computer-implemented mathematical model....
system can be stabilized in exactly the same way as a typical linear state observerState observerIn control theory, a state observer is a system that models a real system in order to provide an estimate of its internal state, given measurements of the input and output of the real system. It is typically a computer-implemented mathematical model....
when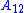 is viewed as the output matrix (i.e., "
is viewed as the output matrix (i.e., " "). That is, the
"). That is, the 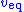 equivalent control provides measurement information about the unmeasured states that can continually move their estimates asymptotically closer to them. Meanwhile, the discontinuous control
equivalent control provides measurement information about the unmeasured states that can continually move their estimates asymptotically closer to them. Meanwhile, the discontinuous control 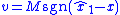 forces the estimate of the measured state to have zero error in finite time. Additionally, white zero-mean symmetric measurement noise (e.g., Gaussian noise) only affects the switching frequency of the control
forces the estimate of the measured state to have zero error in finite time. Additionally, white zero-mean symmetric measurement noise (e.g., Gaussian noise) only affects the switching frequency of the control  , and hence the noise will have little effect on the equivalent sliding mode control
, and hence the noise will have little effect on the equivalent sliding mode control 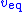 . Hence, the sliding mode observer has Kalman filterKalman filterIn statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
. Hence, the sliding mode observer has Kalman filterKalman filterIn statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
–like features.
The final version of the observer is thus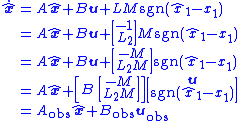
where-
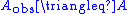 ,
, -
 , and
, and -
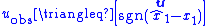 .
.
That is, by augmenting the control vector with the switching function
with the switching function 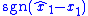 , the sliding mode observer can be implemented as an LTI system. That is, the discontinuous signal
, the sliding mode observer can be implemented as an LTI system. That is, the discontinuous signal 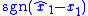 is viewed as a control input to the 2-input LTI system.
is viewed as a control input to the 2-input LTI system.
For simplicity, this example assumes that the sliding mode observer has access to a measurement of a single state (i.e., output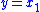 ). However, a similar procedure can be used to design a sliding mode observer for a vector of weighted combinations of states (i.e., when output
). However, a similar procedure can be used to design a sliding mode observer for a vector of weighted combinations of states (i.e., when output 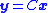 uses a generic matrix
uses a generic matrix  ). In each case, the sliding mode will be the manifold where the estimated output
). In each case, the sliding mode will be the manifold where the estimated output 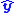 follows the measured output
follows the measured output  with zero error (i.e., the manifold where
with zero error (i.e., the manifold where  ).
).
See also
- Variable structure controlVariable structure controlVariable structure control, or VSC, is a form of discontinuous nonlinear control. The method alters the dynamics of a nonlinear system by application of a high-frequency switching control. The state-feedback control law is not a continuous function of time; it switches from one smooth condition to...
- Variable structure system
- Hybrid systemHybrid systemA hybrid system is a dynamic system that exhibits both continuous and discrete dynamic behavior – a system that can both flow and jump...
- Nonlinear controlNonlinear controlNonlinear control is the area of control engineering specifically involved with systems that are nonlinear, time-variant, or both. Many well-established analysis and design techniques exist for LTI systems ; however, one or both of the controller and the system under control in a general control...
- Robust controlRobust controlRobust control is a branch of control theory that explicitly deals with uncertainty in its approach to controller design. Robust control methods are designed to function properly so long as uncertain parameters or disturbances are within some set...
- Optimal controlOptimal controlOptimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
- Bang–bang control – Sliding mode control is often implemented as a bang–bang control. In some cases, such control is necessary for optimalityOptimal controlOptimal control theory, an extension of the calculus of variations, is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and his collaborators in the Soviet Union and Richard Bellman in the United States.-General method:Optimal...
. - H-bridgeH-bridgeAn H bridge is an electronic circuit that enables a voltage to be applied across a load in either direction. These circuits are often used in robotics and other applications to allow DC motors to run forwards and backwards...
– A topology that combines four switches forming the four legs of an "H". Can be used to drive a motor (or other electrical device) forward or backward when only a single supply is available. Often used in actuator in sliding-mode controlled systems. - Switching amplifierSwitching amplifierA class-D amplifier or switching amplifier is an electronic amplifier where all power devices are operated as binary switches. They are either fully on or fully off. Ideally, zero time is spent transitioning between those two states....
– Uses switching-mode control to drive continuous outputs - Delta-sigma modulationDelta-sigma modulationDelta-sigma modulation is a method for encoding high-resolution or analog signals into lower-resolution digital signals. The conversion is done using error feedback, where the difference between the two signals is measured and used to improve the conversion...
– Another (feedback) method of encoding a continuous range of values in a signal that rapidly switches between two states (i.e., a kind of specialized sliding-mode control) - Pulse density modulation – A generalized form of delta-sigma modulation.
- Pulse-width modulationPulse-width modulationPulse-width modulation , or pulse-duration modulation , is a commonly used technique for controlling power to inertial electrical devices, made practical by modern electronic power switches....
– Another modulation scheme that produces continuous motion through discontinuous switching.
- which can be expressed in closed form
- Also assume that
- where
- Hence, the product
- To ensure
-