
Colombeau algebra
Encyclopedia
In mathematics
, the Colombeau algebra (named for Jean-François Colombeau) is an algebra
introduced with the aim of constructing an improved theory of distribution
s in which multiplication is not problematic. The origins of the theory are in applications to quasilinear hyperbolic partial differential equation
s.
It is defined as a quotient algebra
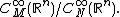
Here the moderate functions on Rn are defined as
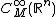
which are families (fε) of smooth function
s on Rn such that
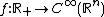
(where R+=(0,∞)) is the set of "regularization
" indices, and for all compact subsets K of Rn and multiindices α we have N > 0 such that

The ideal
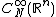
of negligible functions is defined in the same way but with the partial derivatives instead bounded by O(εN) for all N > 0.
with any element of the algebra having as representative a δ-net
, i.e. such that in D' as ε→0.
in D' as ε→0.
This embedding is non-canonical, because it depends on the choice of the δ-net. However, there are versions of Colombeau algebras (so called full algebras) which allow for canonic embeddings of distributions. A well known full version is obtained by adding the mollifiers as second indexing set.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Colombeau algebra (named for Jean-François Colombeau) is an algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
introduced with the aim of constructing an improved theory of distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
s in which multiplication is not problematic. The origins of the theory are in applications to quasilinear hyperbolic partial differential equation
Hyperbolic partial differential equation
In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
s.
It is defined as a quotient algebra
Quotient algebra
In mathematics, a quotient algebra, , also called a factor algebra is obtained by partitioning the elements of an algebra in equivalence classes given by a congruence, that is an equivalence relation that is additionally compatible with all the operations of the algebra, in the formal sense...
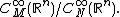
Here the moderate functions on Rn are defined as
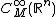
which are families (fε) of smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s on Rn such that
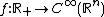
(where R+=(0,∞)) is the set of "regularization
Regularization
Regularization may refer to:* Regularization ** Regularization * Regularization * Regularization * Regularization...
" indices, and for all compact subsets K of Rn and multiindices α we have N > 0 such that

The ideal
Ideal
-In philosophy:* Ideal , values that one actively pursues as goals* Platonic ideal, a philosophical idea of trueness of form, associated with Plato-In mathematics:* Ideal , special subsets of a ring considered in abstract algebra...
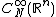
of negligible functions is defined in the same way but with the partial derivatives instead bounded by O(εN) for all N > 0.
Embedding of distributions
The space(s) of Schwartz distributions can be embedded into this simplified algebra by (component-wise) convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
with any element of the algebra having as representative a δ-net
E-net (probability theory)
An \varepsilon-net is any of several related concepts in mathematics, and has a particular meaning in probability theory where it is used in desription of the approximation of one probability distribution by another.- Theory :...
, i.e. such that
 in D' as ε→0.
in D' as ε→0.This embedding is non-canonical, because it depends on the choice of the δ-net. However, there are versions of Colombeau algebras (so called full algebras) which allow for canonic embeddings of distributions. A well known full version is obtained by adding the mollifiers as second indexing set.

