
Operational calculus
Encyclopedia
Operational calculus, also known as operational analysis, is a technique by which problems in analysis
, in particular differential equation
s, are transformed into algebraic problems, usually the problem of solving a polynomial equation.
has a long history that goes back to Gottfried Leibniz
. The mathematician Louis François Antoine Arbogast was one of the first to manipulate these symbols independently of the function to which they were applied.
This approach was further developed by Servois who developed convenient notations. Servois was followed
by a school of British mathematicians including Heargrave, Boole, Bownin, Carmichael, Doukin, Graves, Murphy, William Spottiswoode
and Sylvester.
Treatises describing the application of operator methods to ordinary and partial differential equations were written by George Boole
in 1859 and by Robert Bell Carmichael in 1855.
This technique was fully developed by the physicist Oliver Heaviside
in 1893, in connection with his work on electromagnetism. At the time, Heaviside's methods were not rigorous, and
his work was not further developed by mathematicians.
Operational calculus first found applications in electrical engineering problems, for
the calculation of transients in linear circuits after 1910, under the impulse of Ernst Julius Berg
, John Renshaw Carson
and Vannevar Bush
.
A rigorous mathematical justification of Heaviside's operational methods came only
after the work of Bromwich
that related operational calculus with
Laplace transformation methods (see the books by Jeffreys, by Carslaw or by MacLachlan for a detailed exposition).
Other ways of justifying the operational methods of Heaviside were introduced in the mid 1920's using
integral equation
techniques (as done by Carson) or Fourier transform
ation (as done by Norbert Wiener).
A different approach to operational calculus was developed in the 1930s by Polish mathematician
Jan Mikusinski
, using algebraic reasoning.
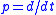 acting on functions.
acting on functions.
Linear differential equations can then be recast in the form of an operator valued function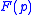 of the operator
of the operator 
acting on the unknown function equals the known function. Solutions are then obtained by making the
inverse operator of act on the known function.
act on the known function.
In electrical circuit theory, one is trying to determine the response of an electrical circuit to
an impulse. Due to linearity, it is enough to consider a unit step, i. e. the function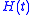 such that
such that  and
and  .
.
The simplest example of application of the operational calculus is to solve: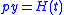 , which gives:
, which gives:
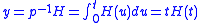 .
.
from this example, one sees that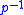 represents integration, and
represents integration, and 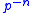
represent iterated integrations. In particular, one has that
iterated integrations. In particular, one has that 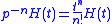 . It is then possible to make sense of
. It is then possible to make sense of 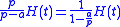 by using a series expansion.
by using a series expansion.
One finds that:
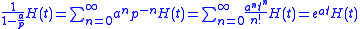
Using [partial fraction] decomposition, it becomes possible to define any fraction in the operator and compute its action on
and compute its action on 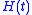 .
.
Moreover, if the function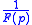 has a series expansion of the form:
has a series expansion of the form:
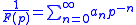 ,
,
it is straightforward to find that:
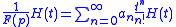
Applying the above rule, solving any linear differential equation is thus reduced to a purely algebraic problem.
Heaviside went farther, and defined fractional power of , thus establishing a connection
, thus establishing a connection
between operational calculus and fractional calculus
.
Using the Taylor expansion, one can also see that , so that operational
, so that operational
calculus is also applicable to finite difference equations and to electrical engineering problems with
delayed signals.
Analysis
Analysis is the process of breaking a complex topic or substance into smaller parts to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle , though analysis as a formal concept is a relatively recent development.The word is...
, in particular differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, are transformed into algebraic problems, usually the problem of solving a polynomial equation.
History
The idea of representing the processes of calculus, derivation and integration, as operatorshas a long history that goes back to Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
. The mathematician Louis François Antoine Arbogast was one of the first to manipulate these symbols independently of the function to which they were applied.
This approach was further developed by Servois who developed convenient notations. Servois was followed
by a school of British mathematicians including Heargrave, Boole, Bownin, Carmichael, Doukin, Graves, Murphy, William Spottiswoode
William Spottiswoode
William Spottiswoode FRS was an English mathematician and physicist. He was President of the Royal Society from 1878 to 1883.-Early life:...
and Sylvester.
Treatises describing the application of operator methods to ordinary and partial differential equations were written by George Boole
George Boole
George Boole was an English mathematician and philosopher.As the inventor of Boolean logic—the basis of modern digital computer logic—Boole is regarded in hindsight as a founder of the field of computer science. Boole said,...
in 1859 and by Robert Bell Carmichael in 1855.
This technique was fully developed by the physicist Oliver Heaviside
Oliver Heaviside
Oliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...
in 1893, in connection with his work on electromagnetism. At the time, Heaviside's methods were not rigorous, and
his work was not further developed by mathematicians.
Operational calculus first found applications in electrical engineering problems, for
the calculation of transients in linear circuits after 1910, under the impulse of Ernst Julius Berg
Ernst Julius Berg
-Biography:Ernst Julius Berg was born in Östersund, Jämtland County in Sweden. After graduating from the Royal Institute of Technology in Stockholm in 1892, he immigrated to the United States. He began working as an assistant to Charles Proteus Steinmetz at General Electric...
, John Renshaw Carson
John Renshaw Carson
John Renshaw Carson , who published as J. R. Carson, was a noted transmission theorist for early communications systems...
and Vannevar Bush
Vannevar Bush
Vannevar Bush was an American engineer and science administrator known for his work on analog computing, his political role in the development of the atomic bomb as a primary organizer of the Manhattan Project, the founding of Raytheon, and the idea of the memex, an adjustable microfilm viewer...
.
A rigorous mathematical justification of Heaviside's operational methods came only
after the work of Bromwich
Thomas John I'Anson Bromwich
Thomas John I'Anson Bromwich was an English mathematician, and a Fellow of the Royal Society. His third name begins with an uppercase i, as opposed to the lowercase L which would seem more likely.-Life:...
that related operational calculus with
Laplace transformation methods (see the books by Jeffreys, by Carslaw or by MacLachlan for a detailed exposition).
Other ways of justifying the operational methods of Heaviside were introduced in the mid 1920's using
integral equation
Integral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
techniques (as done by Carson) or Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
ation (as done by Norbert Wiener).
A different approach to operational calculus was developed in the 1930s by Polish mathematician
Jan Mikusinski
Jan Mikusinski
Prof. Jan Mikusiński was a Polish mathematician known for his pioneering work in mathematical analysis. Mikusiński developed an operational calculus - 44A40 Calculus of Mikusiński, which is relevant for solving differential equations...
, using algebraic reasoning.
Principle
The key element of the operational calculus is to consider differentiation as an operator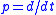 acting on functions.
acting on functions.Linear differential equations can then be recast in the form of an operator valued function
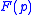 of the operator
of the operator 
acting on the unknown function equals the known function. Solutions are then obtained by making the
inverse operator of
 act on the known function.
act on the known function.In electrical circuit theory, one is trying to determine the response of an electrical circuit to
an impulse. Due to linearity, it is enough to consider a unit step, i. e. the function
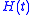 such that
such that  and
and  .
.The simplest example of application of the operational calculus is to solve:
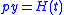 , which gives:
, which gives: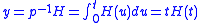 .
.from this example, one sees that
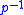 represents integration, and
represents integration, and 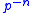
represent
 iterated integrations. In particular, one has that
iterated integrations. In particular, one has that 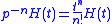 . It is then possible to make sense of
. It is then possible to make sense of 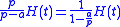 by using a series expansion.
by using a series expansion.One finds that:
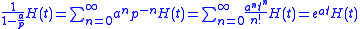
Using [partial fraction] decomposition, it becomes possible to define any fraction in the operator
 and compute its action on
and compute its action on 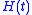 .
.Moreover, if the function
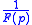 has a series expansion of the form:
has a series expansion of the form: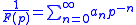 ,
,it is straightforward to find that:
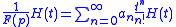
Applying the above rule, solving any linear differential equation is thus reduced to a purely algebraic problem.
Heaviside went farther, and defined fractional power of
 , thus establishing a connection
, thus establishing a connectionbetween operational calculus and fractional calculus
Fractional calculus
Fractional calculus is a branch of mathematical analysis that studies the possibility of taking real number powers or complex number powers of the differentiation operator.and the integration operator J...
.
Using the Taylor expansion, one can also see that
 , so that operational
, so that operationalcalculus is also applicable to finite difference equations and to electrical engineering problems with
delayed signals.

