
Approximate identity
Encyclopedia
In functional analysis
and ring theory, an approximate identity is a net in a Banach algebra or ring (possibly without an identity) that acts as a substitute for an identity element.
More precisely, a right approximate identity in a Banach algebra
, A, is a net
(or a sequence
)

such that for every element, a, of A, the net (or sequence)
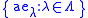
has limit a.
Similarly, a left approximate identity is a net
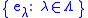
such that for every element, a, of A, the net (or sequence)
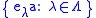
has limit a.
An approximate identity is a right approximate identity which is also a left approximate identity.
For C*-algebras, a right (or left) approximate identity is the same as an approximate identity. Every C*-algebra has an approximate identity of positive elements of norm ≤ 1; indeed, the net of all positive elements of norm ≤ 1; in A with its natural order always suffices. This is called the canonical approximate identity of a C*-algebra. Approximate identities of C*-algebras are not unique. For example, for compact operators acting on a Hilbert space, the net consisting of finite rank projections would be another approximate identity.
An approximate identity in a convolution
algebra plays the same role as a sequence of function approximations to the Dirac delta function
(which is the identity element for convolution). For example the Fejér kernels of Fourier series
theory give rise to an approximate identity.
A module over a ring with approximate identity is called non-degenerate if for every m in the module there is some λ with m=meλ.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and ring theory, an approximate identity is a net in a Banach algebra or ring (possibly without an identity) that acts as a substitute for an identity element.
More precisely, a right approximate identity in a Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
, A, is a net
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
(or a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
)

such that for every element, a, of A, the net (or sequence)
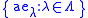
has limit a.
Similarly, a left approximate identity is a net
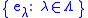
such that for every element, a, of A, the net (or sequence)
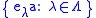
has limit a.
An approximate identity is a right approximate identity which is also a left approximate identity.
For C*-algebras, a right (or left) approximate identity is the same as an approximate identity. Every C*-algebra has an approximate identity of positive elements of norm ≤ 1; indeed, the net of all positive elements of norm ≤ 1; in A with its natural order always suffices. This is called the canonical approximate identity of a C*-algebra. Approximate identities of C*-algebras are not unique. For example, for compact operators acting on a Hilbert space, the net consisting of finite rank projections would be another approximate identity.
An approximate identity in a convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
algebra plays the same role as a sequence of function approximations to the Dirac delta function
Dirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
(which is the identity element for convolution). For example the Fejér kernels of Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
theory give rise to an approximate identity.
Ring theory
In ring theory an approximate identity is defined in a similar way, except that the ring is given the discrete topology so that a=aeλ for some λ.A module over a ring with approximate identity is called non-degenerate if for every m in the module there is some λ with m=meλ.

