Constant sheaf
Encyclopedia
In mathematics
, the constant sheaf on a topological space
X associated to a set A is a sheaf of sets
on X whose stalks
are all equal to A. It is denoted by or AX. The constant presheaf with value A is the presheaf that assigns to each open subset
of X the value A, and all of whose restriction maps are the identity map . The constant sheaf associated to A is the sheafification of the constant presheaf associated to A.
In certain cases, the set A may be replaced with an object A in some category
C (e.g. when C is the category of abelian groups
, or commutative rings).
Constant sheaves of abelian group
s appear in particular as coefficients in sheaf cohomology
.
, then these locally constant functions are constant. If f: X → {pt} is the unique map
to the one-point space and A is considered as a sheaf on {pt}, then the inverse image f−1A is the constant sheaf on X. The sheaf space of is the projection map X × A → X (where A is given the discrete topology).
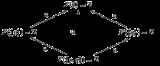
Let X be the topological space consisting of two points p and q with the discrete topology. X has four open sets: ∅, {p}, {q}, }. The five non-trivial inclusions of the open sets of X are shown in the chart.
A presheaf on X chooses a set for each of the four open sets of X and a restriction map for each of the nine inclusions (five non-trivial inclusions and four trivial ones). The constant presheaf with value Z, which we will denote F, is the presheaf which chooses all four sets to be Z, the integers, and all restriction maps to be the identity. F is a functor, hence a presheaf, because it is constant. Each of the restriction maps is injective, so F is a separated presheaf. F satisfies the gluing axiom, but it is not a sheaf because it fails the local identity axiom on the empty set. This is because the empty set is covered by the empty family of sets: Vacuously, any two sections of F over the empty set are equal when restricted to any set in the empty family. The local identity axiom would therefore imply that any two sections of F over the empty set are equal, but this is not true.
A similar presheaf G which satisfies the local identity axiom over the empty set is constructed as follows. Let , where 0 is a one-element set. On all non-empty sets, give G the value Z. For each inclusion of open sets, G returns either the unique map to 0, if the smaller set is empty, or the identity map on Z.
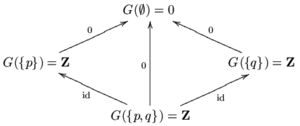Notice that as a consequence of the local identity axiom for the empty set, all the restriction maps involving the empty set are boring. This is true for any presheaf satisfying the local identity axiom for the empty set, and in particular for any sheaf.
G is a separated presheaf which satisfies the local identity axiom, but unlike F it fails the gluing axiom. } is covered by the two open sets {p} and {q}, and these sets have empty intersection. A section on {p} or on {q} is an element of Z, that is, it is a number. Choose a section m over {p} and n over {q}, and assume that . Because m and n restrict to the same element 0 over ∅, the gluing axiom requires the existence of a unique section s on which restricts to m on {p} and n on {q}. But because the restriction map from } to {p} is the identity, , and similarly , so , a contradiction.
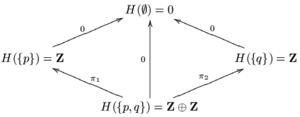is too small to carry information about both {p} and {q}. To enlarge it so that it satisfies the gluing axiom, let . Let π1 and π2 be the two projection maps . Define and . For the remaining open sets and inclusions, let H equal G. H is a sheaf called the constant sheaf on X with value Z. Because Z is a ring and all the restriction maps are ring homomorphisms, H is a sheaf of commutative rings.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the constant sheaf on a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X associated to a set A is a sheaf of sets
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
on X whose stalks
Stalk (sheaf)
The stalk of a sheaf is a mathematical construction capturing the behaviour of a sheaf around a given point.-Motivation and definition:Sheaves are defined on open sets, but the underlying topological space X consists of points. It is reasonable to attempt to isolate the behavior of a sheaf at a...
are all equal to A. It is denoted by or AX. The constant presheaf with value A is the presheaf that assigns to each open subset
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of X the value A, and all of whose restriction maps are the identity map . The constant sheaf associated to A is the sheafification of the constant presheaf associated to A.
In certain cases, the set A may be replaced with an object A in some category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
C (e.g. when C is the category of abelian groups
Category of abelian groups
In mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
, or commutative rings).
Constant sheaves of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s appear in particular as coefficients in sheaf cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
.
Basics
Let X be a topological space, and A a set. The sections of the constant sheaf over an open set U may be interpreted as the continuous functions , where A is given the discrete topology. If U is connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, then these locally constant functions are constant. If f: X → {pt} is the unique map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
to the one-point space and A is considered as a sheaf on {pt}, then the inverse image f−1A is the constant sheaf on X. The sheaf space of is the projection map X × A → X (where A is given the discrete topology).
A detailed example
A presheaf on X chooses a set for each of the four open sets of X and a restriction map for each of the nine inclusions (five non-trivial inclusions and four trivial ones). The constant presheaf with value Z, which we will denote F, is the presheaf which chooses all four sets to be Z, the integers, and all restriction maps to be the identity. F is a functor, hence a presheaf, because it is constant. Each of the restriction maps is injective, so F is a separated presheaf. F satisfies the gluing axiom, but it is not a sheaf because it fails the local identity axiom on the empty set. This is because the empty set is covered by the empty family of sets: Vacuously, any two sections of F over the empty set are equal when restricted to any set in the empty family. The local identity axiom would therefore imply that any two sections of F over the empty set are equal, but this is not true.
A similar presheaf G which satisfies the local identity axiom over the empty set is constructed as follows. Let , where 0 is a one-element set. On all non-empty sets, give G the value Z. For each inclusion of open sets, G returns either the unique map to 0, if the smaller set is empty, or the identity map on Z.
G is a separated presheaf which satisfies the local identity axiom, but unlike F it fails the gluing axiom. } is covered by the two open sets {p} and {q}, and these sets have empty intersection. A section on {p} or on {q} is an element of Z, that is, it is a number. Choose a section m over {p} and n over {q}, and assume that . Because m and n restrict to the same element 0 over ∅, the gluing axiom requires the existence of a unique section s on which restricts to m on {p} and n on {q}. But because the restriction map from } to {p} is the identity, , and similarly , so , a contradiction.