Topological K-theory
Encyclopedia
In mathematics
, topological K-theory is a branch of algebraic topology
. It was founded to study vector bundle
s on general topological space
s, by means of ideas now recognised as (general) K-theory
that were introduced by Alexander Grothendieck
. The early work on topological K-theory is due to Michael Atiyah
and Friedrich Hirzebruch
.
or 
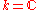. Then 
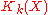is the Grothendieck group
of the commutative monoid whose elements are the isomorphism class
es of finite dimensional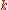
-vector bundles on X with the operation
for vector bundles E, F. Usually,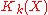
is denoted 
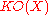in real case and 
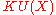in the complex case.
More explicitly, stable equivalence, the equivalence relation
on bundles E and F on X of defining the same element in K(X), occurs when there is a trivial bundle G, so that
.
Under the tensor product of vector bundles K(X) then becomes a commutative ring
.
The rank of a vector bundle carries over to the K-group. Define the homomorphism
where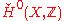
is the 0-group of Čech cohomology
which is equal to the group of locally constant functions with values in
.
If X has a distinguished basepoint
x0, then the reduced K-group (cf. reduced homology
) satisfies
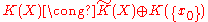
and is defined as either the kernel
of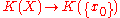
(where 
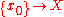is basepoint inclusion) or the cokernel
of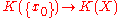
(where 
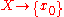is the constant map).
When X is a connected space
,
.
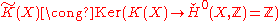The definition of the functor
K extends to the category
of pairs of compact space
s (in this category, an object is a pair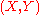
, where 
is compact and 
is closed, a morphism
between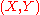
and 
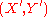is a continuous map 
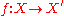such that 
)
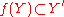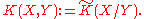
The reduced K-group is given by
.
The definition
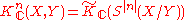
gives the sequence of K-groups for
, where S denotes the reduced suspension.
named for Raoul Bott
(see Bott periodicity theorem
) can be formulated this way:
In real K-theory there is a similar periodicity, but modulo 8.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, topological K-theory is a branch of algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
. It was founded to study vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
s on general topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s, by means of ideas now recognised as (general) K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
that were introduced by Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
. The early work on topological K-theory is due to Michael Atiyah
Michael Atiyah
Sir Michael Francis Atiyah, OM, FRS, FRSE is a British mathematician working in geometry.Atiyah grew up in Sudan and Egypt but spent most of his academic life in the United Kingdom at Oxford and Cambridge, and in the United States at the Institute for Advanced Study...
and Friedrich Hirzebruch
Friedrich Hirzebruch
Friedrich Ernst Peter Hirzebruch is a German mathematician, working in the fields of topology, complex manifolds and algebraic geometry, and a leading figure in his generation.-Life:He was born in Hamm, Westphalia...
.
Definitions
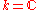Let X be a compact Hausdorff space and or . Then 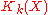is the Grothendieck groupGrothendieck group
In mathematics, the Grothendieck group construction in abstract algebra constructs an abelian group from a commutative monoid in the best possible way...
of the commutative monoid whose elements are the isomorphism class
Isomorphism class
An isomorphism class is a collection of mathematical objects isomorphic to each other.Isomorphism classes are often defined if the exact identity of the elements of the set is considered irrelevant, and the properties of the structure of the mathematical object are studied. Examples of this are...
es of finite dimensional
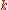-vector bundles on X with the operationfor vector bundles E, F. Usually,
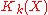is denoted 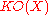in real case and 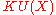in the complex case.More explicitly, stable equivalence, the equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on bundles E and F on X of defining the same element in K(X), occurs when there is a trivial bundle G, so that
.Under the tensor product of vector bundles K(X) then becomes a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
.
The rank of a vector bundle carries over to the K-group. Define the homomorphism
where
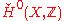is the 0-group of Čech cohomologyCech cohomology
In mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.-Motivation:...
which is equal to the group of locally constant functions with values in
.If X has a distinguished basepoint
Pointed space
In mathematics, a pointed space is a topological space X with a distinguished basepoint x0 in X. Maps of pointed spaces are continuous maps preserving basepoints, i.e. a continuous map f : X → Y such that f = y0...
x0, then the reduced K-group (cf. reduced homology
Reduced homology
In mathematics, reduced homology is a minor modification made to homology theory in algebraic topology, designed to make a point have all its homology groups zero...
) satisfies
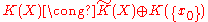
and is defined as either the kernel
Kernel (category theory)
In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
of
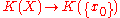(where 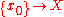is basepoint inclusion) or the cokernelCokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
of
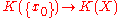(where 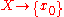is the constant map).When X is a connected space
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
,
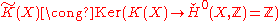.The definition of the functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
K extends to the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of pairs of compact space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
s (in this category, an object is a pair
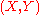, where is compact and is closed, a morphismMorphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
between
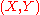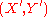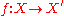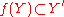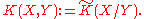
and is a continuous map such that )The reduced K-group is given by
.The definition
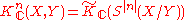
gives the sequence of K-groups for
, where S denotes the reduced suspension.Properties
-
is a contravariant functor. - The classifying spaceClassifying spaceIn mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
of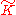
is 
(BO, in real case; BU in complex case), i.e. 
- The classifying spaceClassifying spaceIn mathematics, specifically in homotopy theory, a classifying space BG of a topological group G is the quotient of a weakly contractible space EG by a free action of G...
of
is 
(
with discrete topology), i.e.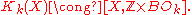 
- There is a natural ring homomorphismRing homomorphismIn ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
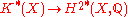, the Chern character, such that 
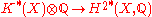is an isomorphism. - Topological K-theory can be generalized vastly to a functor on C*-algebras, see operator K-theoryOperator K-theoryIn mathematics, operator K-theory is a variant of K-theory on the category of Banach algebras ....
and KK-theoryKK-theoryIn mathematics, KK-theory is a common generalization both of K-homology and K-theory , as an additive bivariant functor on separable C*-algebras...
.
Bott periodicity
The phenomenon of periodicityFrequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
named for Raoul Bott
Raoul Bott
Raoul Bott, FRS was a Hungarian mathematician known for numerous basic contributions to geometry in its broad sense...
(see Bott periodicity theorem
Bott periodicity theorem
In mathematics, the Bott periodicity theorem describes a periodicity in the homotopy groups of classical groups, discovered by , which proved to be of foundational significance for much further research, in particular in K-theory of stable complex vector bundles, as well as the stable homotopy...
) can be formulated this way:
-
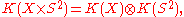and 
where 
is the class of the tautological bundleTautological bundleIn mathematics, tautological bundle is a term for a particularly natural vector bundle occurring over a Grassmannian, and more specially over projective space...
on the
, i.e. the Riemann sphereRiemann sphereIn mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
as complex projective line. -
-
In real K-theory there is a similar periodicity, but modulo 8.