Pointed space
Encyclopedia
In mathematics
, a pointed space is a topological space
X with a distinguished basepoint x0 in X. Maps of pointed spaces (based maps) are continuous maps preserving basepoints, i.e. a continuous map f : X → Y such that f(x0) = y0. This is usually denoted
Pointed spaces are important in algebraic topology
, particularly in homotopy theory, where many constructions, such as the fundamental group
, depend on a choice of basepoint.
The pointed set
concept is less important; it is anyway the case of a pointed discrete space
.
of all pointed spaces forms a category
Top• with basepoint preserving continuous maps as morphism
s. Another way to think about this category is as the comma category
, ({•} ↓ Top) where {•} is any one point space and Top is the category of topological spaces
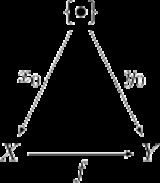
. (This is also called a coslice category denoted {•}/Top.) Objects in this category are continuous maps {•} → X. Such morphisms can be thought of as picking out a basepoint in X. Morphisms in ({•} ↓ Top) are morphisms in Top for which the following diagram commutes
:
It is easy to see that commutativity of the diagram is equivalent to the condition that f preserves basepoints.
As a pointed space {•} is a zero object in Top• while it is only a terminal object in Top.
There is a forgetful functor
Top• → Top which "forgets" which point is the basepoint. This functor has a left adjoint which assigns to each topological space X the disjoint union
of X and a one point space {•} whose single element is taken to be the basepoint.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a pointed space is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X with a distinguished basepoint x0 in X. Maps of pointed spaces (based maps) are continuous maps preserving basepoints, i.e. a continuous map f : X → Y such that f(x0) = y0. This is usually denoted
- f : (X, x0) → (Y, y0).
Pointed spaces are important in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, particularly in homotopy theory, where many constructions, such as the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
, depend on a choice of basepoint.
The pointed set
Pointed set
In mathematics, a pointed set is a set X with a distinguished element x_0\in X, which is called the basepoint. Maps of pointed sets are those functions that map one basepoint to another, i.e. a map f : X \to Y such that f = y_0. This is usually denotedf : \to .Pointed sets may be regarded as a...
concept is less important; it is anyway the case of a pointed discrete space
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
.
Category of pointed spaces
The classClass (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
of all pointed spaces forms a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
Top• with basepoint preserving continuous maps as morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s. Another way to think about this category is as the comma category
Comma category
In mathematics, a comma category is a construction in category theory. It provides another way of looking at morphisms: instead of simply relating objects of a category to one another, morphisms become objects in their own right. This notion was introduced in 1963 by F. W...
, ({•} ↓ Top) where {•} is any one point space and Top is the category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
. (This is also called a coslice category denoted {•}/Top.) Objects in this category are continuous maps {•} → X. Such morphisms can be thought of as picking out a basepoint in X. Morphisms in ({•} ↓ Top) are morphisms in Top for which the following diagram commutes
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:
It is easy to see that commutativity of the diagram is equivalent to the condition that f preserves basepoints.
As a pointed space {•} is a zero object in Top• while it is only a terminal object in Top.
There is a forgetful functor
Forgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
Top• → Top which "forgets" which point is the basepoint. This functor has a left adjoint which assigns to each topological space X the disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of X and a one point space {•} whose single element is taken to be the basepoint.
Operations on pointed spaces
- A subspace of a pointed space X is a topological subspace A ⊆ X which shares its basepoint with X so that the inclusion mapInclusion mapIn mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
is basepoint preserving. - One can form the quotientQuotient spaceIn topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
of a pointed space X under any equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
. The basepoint of the quotient is the image of the basepoint in X under the quotient map. - One can form the productProduct (category theory)In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
of two pointed spaces (X, x0), (Y, y0) as the topological product X × Y with (x0, y0) serving as the basepoint. - The coproductCoproductIn category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
in the category of pointed spaces is the wedge sumWedge sumIn topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces the wedge sum of X and Y is the quotient of the disjoint union of X and Y by the identification x0 ∼ y0:X\vee Y = \;/ \sim,\,where ∼ is the...
, which can be thought of as the one-point union of spaces. - The smash productSmash productIn mathematics, the smash product of two pointed spaces X and Y is the quotient of the product space X × Y under the identifications ∼ for all x ∈ X and y ∈ Y. The smash product is usually denoted X ∧ Y...
of two pointed spaces is essentially the quotientQuotient spaceIn topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
of the direct product and the wedge sum. The smash product turns the category of pointed spaces into a symmetric monoidal category with the pointed 0-sphere as the unit object. - The reduced suspension ΣX of a pointed space X is (up to a homeomorphismHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
) the smash product of X and the pointed circle S1. - The reduced suspension is a functor from the category of pointed spaces to itself. This functor is a left adjoint to the functor
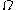 taking a based space
taking a based space 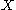 to its loop space
to its loop space 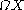 .
.

