Pointed set
Encyclopedia
In mathematics
, a pointed set is a set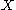
with a distinguished element 
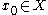, which is called the basepoint. Maps of pointed sets (based maps) are those functions
that map one basepoint to another, i.e. a map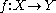
such that 
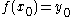. This is usually denoted
.
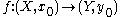Pointed sets may be regarded as a rather simple algebraic structure
. In the sense of universal algebra
, they are structures with a single nullary operation which picks out the basepoint.
The class
of all pointed sets together with the class of all based maps form a category
.
A pointed set may be seen as a pointed space
under the discrete topology or as a vector space
over the field with one element
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a pointed set is a set
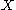with a distinguished element 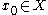, which is called the basepoint. Maps of pointed sets (based maps) are those functionsFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that map one basepoint to another, i.e. a map
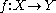such that 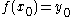. This is usually denoted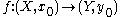.Pointed sets may be regarded as a rather simple algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
. In the sense of universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
, they are structures with a single nullary operation which picks out the basepoint.
The class
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
of all pointed sets together with the class of all based maps form a category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
.
A pointed set may be seen as a pointed space
Pointed space
In mathematics, a pointed space is a topological space X with a distinguished basepoint x0 in X. Maps of pointed spaces are continuous maps preserving basepoints, i.e. a continuous map f : X → Y such that f = y0...
under the discrete topology or as a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over the field with one element
Field with one element
In mathematics, the field with one element is a suggestive name for an object that should behave similarly to a finite field with a single element, if such a field could exist. This object is denoted F1, or, in a French-English pun, Fun...
.