Symmetry of second derivatives
Encyclopedia
In mathematics
, the symmetry of second derivatives (also called the equality of mixed partials) refers to the possibility of interchanging the order of taking partial derivative
s of a function
of n variables. If the partial derivative with respect to
is denoted with a subscript 
, then the symmetry is the assertion that the second-order partial derivatives 
satisfy the identity
so that they form an n × n symmetric matrix. This is sometimes known as Young's theorem.
This property may also be considered as a condition
for the function
to be single-valued. Then it is called the
Schwarz integrability condition. In physics, however, it is important
for the understanding of many phenomena in nature to remove this restrictions and allow functions to violate the
Schwarz integrability criterion, which makes them multivalued.
The simplest example is the function
. At first one defines this with a cut
in the complex
-plane running from 0 to infinity.
The cut makes the function single-valued. In complex analysis, however, one thinks of this function as having several 'sheets' (forming a Riemann surface
).
of f. The entries in it off the main diagonal are the mixed derivatives; that is, successive partial derivatives with respect to different variables.
In most circumstances the Hessian matrix is symmetric. Mathematical analysis
reveals that symmetry requires a hypothesis on f that goes further than simply stating the existence of the second derivatives at a particular point. Clairaut's theorem
gives a sufficient condition on f for this to occur.
This equality can also be written as
Alternatively, the symmetry can be written as an algebraic statement involving the differential operator
Di which takes the partial derivative with respect to xi:
From this relation it follows that the ring
of differential operators with constant coefficients
, generated by the Di, is commutative. But one should naturally specify some domain for these operators. It is easy to check the symmetry as applied to monomial
s, so that one can take polynomial
s in the xi as a domain. In fact smooth function
s are possible.
, Clairaut's theorem or Schwarz's theorem, named after Alexis Clairaut and Hermann Schwarz
, states that if
has continuous
second partial derivatives at any given point in
, say, 
then for 
In words, the partial derivations of this function are commutative at that point. One easy way to establish this theorem (in the case where n = 2, i = 1, and j = 2, which readily entails the result in general) is by applying Green's theorem
to the gradient
of f.
s eliminates analytic problems with the symmetry. The derivative of any integrable function can be defined as a distribution. The use of integration by parts
puts the symmetry question back onto the test functions, which are smooth and certainly satisfy the symmetry. In the sense of distributions, symmetry always holds.
Another approach, which defines the Fourier transform
of a function, is to note that on such transforms partial derivatives become multiplication operators that commute much more obviously.
corresponding to making h → 0 first, and to making k → 0 first. These processes need not commute (see interchange of limiting operations
): it can matter, looking at the first-order terms, which is applied first. This leads to the construction of pathological
examples in which second derivatives are non-symmetric. Given that the derivatives as Schwartz distributions are symmetric, this kind of example belongs in the 'fine' theory of real analysis
.
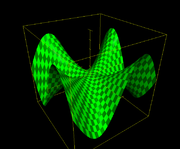The following example displays non-symmetry. Note that it does not violate Clairaut's theorem since the derivatives are not continuous at (0,0)
The mixed partial derivatives of f exist and are continuous everywhere except at
. Moreover
at
.
. That is, Di in a sense generates the one-parameter group
of translation
s parallel to the xi-axis. These groups commute with each other, and therefore the infinitesimal generators do also; the Lie bracket
is this property's reflection. In other words, the Lie derivative of one coordinate with respect to another is zero.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the symmetry of second derivatives (also called the equality of mixed partials) refers to the possibility of interchanging the order of taking partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of a function
of n variables. If the partial derivative with respect to
is denoted with a subscript , then the symmetry is the assertion that the second-order partial derivatives satisfy the identityso that they form an n × n symmetric matrix. This is sometimes known as Young's theorem.
This property may also be considered as a condition
for the function
to be single-valued. Then it is called the
Schwarz integrability condition. In physics, however, it is important
for the understanding of many phenomena in nature to remove this restrictions and allow functions to violate the
Schwarz integrability criterion, which makes them multivalued.
The simplest example is the function
. At first one defines this with a cutin the complex
-plane running from 0 to infinity.The cut makes the function single-valued. In complex analysis, however, one thinks of this function as having several 'sheets' (forming a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
).
Hessian matrix
This matrix of second-order partial derivatives of f is called the Hessian matrixHessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
of f. The entries in it off the main diagonal are the mixed derivatives; that is, successive partial derivatives with respect to different variables.
In most circumstances the Hessian matrix is symmetric. Mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
reveals that symmetry requires a hypothesis on f that goes further than simply stating the existence of the second derivatives at a particular point. Clairaut's theorem
Clairaut's theorem
Clairaut's theorem, published in 1743 by Alexis Claude Clairaut in his Théorie de la figure de la terre, tirée des principes de l'hydrostatique, synthesized physical and geodetic evidence that the Earth is an oblate rotational ellipsoid. It is a general mathematical law applying to spheroids of...
gives a sufficient condition on f for this to occur.
Formal expressions of symmetry
In symbols, the symmetry says that, for example,This equality can also be written as
Alternatively, the symmetry can be written as an algebraic statement involving the differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
Di which takes the partial derivative with respect to xi:
- Di . Dj = Dj . Di.
From this relation it follows that the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of differential operators with constant coefficients
Constant coefficients
In mathematics, constant coefficients is a term applied to differential operators, and also some difference operators, to signify that they contain no functions of the independent variables, other than constant functions. In other words, it singles out special operators, within the larger class of...
, generated by the Di, is commutative. But one should naturally specify some domain for these operators. It is easy to check the symmetry as applied to monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
s, so that one can take polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in the xi as a domain. In fact smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s are possible.
Clairaut's theorem
In mathematical analysisMathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, Clairaut's theorem or Schwarz's theorem, named after Alexis Clairaut and Hermann Schwarz
Hermann Schwarz
Karl Hermann Amandus Schwarz was a German mathematician, known for his work in complex analysis. He was born in Hermsdorf, Silesia and died in Berlin...
, states that if
has continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
second partial derivatives at any given point in
, say, then for In words, the partial derivations of this function are commutative at that point. One easy way to establish this theorem (in the case where n = 2, i = 1, and j = 2, which readily entails the result in general) is by applying Green's theorem
Green's theorem
In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
to the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of f.
Distribution theory formulation
The theory of distributionDistribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
s eliminates analytic problems with the symmetry. The derivative of any integrable function can be defined as a distribution. The use of integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
puts the symmetry question back onto the test functions, which are smooth and certainly satisfy the symmetry. In the sense of distributions, symmetry always holds.
Another approach, which defines the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of a function, is to note that on such transforms partial derivatives become multiplication operators that commute much more obviously.
Non-symmetry
In the worst case symmetry fails. Given two variables near (0, 0) and two limiting processes oncorresponding to making h → 0 first, and to making k → 0 first. These processes need not commute (see interchange of limiting operations
Interchange of limiting operations
In mathematics, the study of interchange of limiting operations is one of the major concerns of mathematical analysis. in that two given limiting operations, say L and M, cannot be assumed to give the same result when applied in either order...
): it can matter, looking at the first-order terms, which is applied first. This leads to the construction of pathological
Pathological (mathematics)
In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....
examples in which second derivatives are non-symmetric. Given that the derivatives as Schwartz distributions are symmetric, this kind of example belongs in the 'fine' theory of real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
.
The mixed partial derivatives of f exist and are continuous everywhere except at
. Moreoverat
.In Lie theory
Consider the first-order differential operators Di to be infinitesimal operators on Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. That is, Di in a sense generates the one-parameter group
One-parameter group
In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphismfrom the real line R to some other topological group G...
of translation
Translation
Translation is the communication of the meaning of a source-language text by means of an equivalent target-language text. Whereas interpreting undoubtedly antedates writing, translation began only after the appearance of written literature; there exist partial translations of the Sumerian Epic of...
s parallel to the xi-axis. These groups commute with each other, and therefore the infinitesimal generators do also; the Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
- [Di, Dj] = 0
is this property's reflection. In other words, the Lie derivative of one coordinate with respect to another is zero.