In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, runcination is an operation that cuts a regular polytope

Regular polytope

In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...

 (or honeycomb

Honeycomb (geometry)

In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....

) simultaneously along the faces, edges and vertices, creating new facets in place of the original face, edge, and vertex centers.

It is a higher order truncation operation, following cantellation

Cantellation (geometry)

In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs...

, and truncation

Truncation (geometry)

In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...

.

It is represented by an extended Schläfli symbol t_0,3{p,q,...}. This operation only exists for 4-polytopes {p,q,r} or higher.

This operation is dual-symmetric for regular polychora

Uniform polychoron

In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

 and 3-space convex uniform honeycomb

Convex uniform honeycomb

In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;...

s.

For a regular {p,q,r} polychoron, the original {p,q} cells remain, but become separated. The gaps at the separated faces become p-gonal prisms

Prism (geometry)

In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...

. The gaps between the separated edges become r-gonal prisms. The gaps between the separated vertices become {r,q} cells. The vertex figure

Vertex figure

In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...

 for a regular 4-polytope {p,q,r} is an q-gonal antiprism

Antiprism

In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...

 (called an antipodium if p and r are different).

For regular polychora/honeycombs, this operation is also called expansion

Expansion (geometry)

In geometry, expansion is a polytope operation where facets are separated and moved radially apart, and new facets are formed at separated elements...

by Alicia Boole Stott

Alicia Boole Stott

Alicia Boole Stott was the third daughter of George Boole and Mary Everest Boole, born in Cork, Ireland. Before marrying Walter Stott, an actuary, in 1890, she was known as Alicia Boole...

, as imagined by taking the cells of the regular form moving them away from the center and filling in new faces in the gaps for each opened vertex and edge.

Runcinated polychoron/honeycombs forms:

Schläfli symbol Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...	Name	Vertex figure Vertex figure In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...	Image
Uniform polychora Uniform polychoron In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
t0,3{3,3,3}	Runcinated 5-cell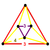
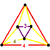
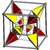
t0,3{3,3,4}	Runcinated 16-cell (Same as runcinated 8-cell)
t0,3{3,4,3}	Runcinated 24-cell Runcinated 24-cell In four-dimensional geometry, a runcinated 24-cell is a convex uniform polychoron, being a runcination of the regular 24-cell....
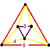
t0,3{3,3,5}	Runcinated 120-cell Runcinated 120-cell In four-dimensional geometry, a runcinated 120-cell is a convex uniform polychoron, being a runcination of the regular 120-cell.... (Same as runcinated 600-cell)
Euclidean convex uniform honeycomb Convex uniform honeycomb In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;... s
t0,3{4,3,4}	Runcinated cubic honeycomb (Same as cubic honeycomb Cubic honeycomb The cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron.... )
Hyperbolic uniform honeycombs Convex uniform honeycombs in hyperbolic space In geometry, a convex uniform honeycomb is a tessellation of convex uniform polyhedron cells. In 3-dimensional hyperbolic space there are nine Coxeter group families of compact convex uniform honeycombs, generated as Wythoff constructions, and represented by ring permutations of the Coxeter–Dynkin...
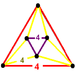
t0,3{4,3,5}	Runcinated order-5 cubic honeycomb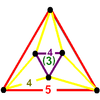
t0,3{3,5,3}	Runcinated icosahedral honeycomb
t0,3{5,3,5}	Runcinated order-5 dodecahedral honeycomb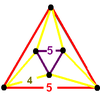

See also

• uniform polyhedron
  Uniform polyhedron
  A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
  
  
• uniform polychoron
  Uniform polychoron
  In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
  
  
• Rectification (geometry)
  Rectification (geometry)
  In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...
  
  
• Truncation (geometry)
  Truncation (geometry)
  In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
  
  
• Cantellation (geometry)
  Cantellation (geometry)
  In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs...