Projective polyhedron
Encyclopedia
In geometry
, a (globally) projective polyhedron is a tessellation
of the real projective plane
. These are projective analogs of spherical polyhedra – tessellations of the sphere
– and toroidal polyhedra – tessellations of the toroids.
Projective polyhedra are also referred to as elliptic tessellations or elliptic tilings, referring to the projective plane as (projective) elliptic geometry
, by analogy with spherical tiling, a synonym for "spherical polyhedron". However, the term elliptic geometry
applies to both spherical and projective geometries, so the term carries some ambiguity for polyhedra.
As cellular decomposition
s of the projective plane, they have Euler characteristic
1, while spherical polyhedra have Euler characteristic 2. The qualifier "globally" is to contrast with locally projective polyhedra, which are defined in the theory of abstract polyhedra.
Non-overlapping projective polyhedra (density
1) correspond to spherical polyhedra (equivalently, convex polyhedra) with central symmetry. This is elaborated and extended below in relation with spherical polyhedra and relation with traditional polyhedra.
The best-known examples of projective polyhedra are the regular projective polyhedra, the quotients of the centrally symmetric Platonic solid
s:
These can be obtained by taking the quotient of the associated spherical polyhedron by the antipodal map (identifying opposite points on the sphere).
On the other hand, the tetrahedron does not have central symmetry, so there is no "hemi-tetrahedron". See relation with spherical polyhedra below on how the tetrahedron is treated.
Note that the prefix "hemi-" is also used to refer to hemipolyhedra, which are uniform polyhedra having some faces that pass through the center of symmetry. As these do not define spherical polyhedra (because they pass through the center, which does not map to a defined point on the sphere), they do not define projective polyhedra by the quotient map from 3-space (minus the origin) to the projective plane.
Of these uniform hemipolyhedra, only the tetrahemihexahedron
is topologically a projective polyhedron, as can be verified by its Euler characteristic
and visually obvious connection to the Roman surface
. It is 2-covered by the cuboctahedron
, and can be realized as the quotient of the spherical cuboctahedron by the antipodal map. It is the only uniform (traditional) polyhedron that is projective – that is, the only uniform projective polyhedron that immerses in Euclidean three-space as a uniform traditional polyhedron.
of the sphere to the projective plane, and under this map, projective polyhedra correspond to spherical polyhedra with central symmetry – the 2-fold cover of a projective polyhedron is a centrally symmetric spherical polyhedron. Further, because a covering map
is a local homeomorphism
(in this case a local isometry), both the spherical and the corresponding projective polyhedra have the same abstract vertex figure.
For example, the 2-fold cover of the (projective) hemi-cube is the (spherical) cube. The hemi-cube has 4 vertices, 3 faces, and 6 edges, each of which is covered by 2 copies in the sphere, and accordingly the cube has 8 vertices, 6 faces, and 12 edges, while both these polyhedra have a 4.4.4 vertex figure (3 squares meeting at a vertex).
Further, the symmetry group (of isometries) of a projective polyhedron and covering spherical polyhedron are related: the symmetries of the projective polyhedron are naturally identified with the rotation symmetries of the spherical polyhedron, while the full symmetry group of the spherical polyhedron is the product of its rotation group (the symmetry group of the projective polyhedron) and the cyclic group of order 2, {±I}. See symmetry group below for elaboration and other dimensions.
Spherical polyhedra without central symmetry do not define a projective polyhedron, as the images of vertices, edges, and faces will overlap. In the language of tilings, the image in the projective plane is a degree 2 tiling, meaning that it covers the projective plane twice – rather than 2 faces in the sphere corresponding to 1 face in the projective plane, covering it twice, each face in the sphere corresponds to a single face in the projective plane, accordingly covering it twice.
The correspondence between projective polyhedra and centrally symmetric spherical polyhedra can be extended to a Galois connection
including all spherical polyhedra (not necessarily centrally symmetric) if the classes are extended to include degree 2 tilings of the projective plane, whose covers are not polyhedra but rather the polyhedral compound
of a non-centrally symmetric polyhedron, together with its central inverse (a compound of 2 polyhedra). This geometrizes the Galois connection at the level of finite subgroups of O(3) and PO(3), under which the adjunction is "union with central inverse". For example, the tetrahedron is not centrally symmetric, and has 4 vertices, 6 edges, and 4 faces, and vertex figure 3.3.3 (3 triangles meeting at each vertex). Its image in the projective plane has 4 vertices, 6 edges (which intersect), and 4 faces (which overlap), covering the projective plane twice. The cover of this is the stellated octahedron – equivalently, the compound of two tetrahedra – which has 8 vertices, 12 edges, and 8 faces, and vertex figure 3.3.3.
s, one instead refers to "locally projective polytopes" – see Abstract polytope: Local topology. For example, the 11-cell
is a "locally projective polytope", but is not a globally projective polyhedron, nor indeed tessellates any manifold, as it not locally Euclidean, but rather locally projective, as the name indicates.
Projective polytopes can be defined in higher dimension as tessellations of projective space in one less dimension. Defining k-dimensional projective polytopes in n-dimensional projective space is somewhat trickier, because the usual definition of polytopes in Euclidean space requires taking convex combination
s of points, which is not a projective concept, and is infrequently addressed in the literature, but has been defined, such as in .
, finite and discrete sets are identical – infinite sets have an accumulation point. subgroup of the projective orthogonal group
, PO, and conversely every finite subgroup of PO is the symmetry group of a projective polytope by taking the polytope given by images of a fundamental domain
for the group.
The relevant dimensions are as follows: n-dimensional real projective space is the projectivization of (n+1)-dimensional Euclidean space
,
so the projective orthogonal group of an n-dimensional projective space is denoted
If n=2k is even (so n+1 = 2k+1 is odd), then O(2k+1) = SO(2k+1)×{±I} decomposes as a product, and thus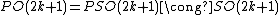
The isomorphism
/equality distinction in this equation is because the context is the 2-to-1 quotient map
– PSO(2k+1) and PO(2k+1) are equal subsets of the target (namely, the whole space), hence the equality, while the induced map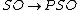 
is an isomorphism but the two groups are subsets of different spaces, hence the isomorphism rather than an equality.
See for an example of this distinction being made. so the group of projective isometries can be identified with the group of rotational isometries.
Thus in particular the symmetry group of a projective polyhedron is the rotational symmetry group of the covering spherical polyhedron; the full symmetry group of the spherical polyhedron is then just the direct product with reflection through the origin, which is the kernel on passage to projective space. The projective plane is non-orientable, and thus there is no distinct notion of "orientation-preserving isometries of a projective polyhedron", which is reflected in the equality PSO(3) = PO(3).
If n=2k + 1 is odd, then O(n+1) = O(2k+2) does not decompose as a product, and thus the symmetry group of the projective polytope is not simply the rotational symmetries of the spherical polytope, but rather a 2-to-1 quotient of the full symmetry group of the corresponding spherical polytope (the spherical group is a central extension
of the projective group). Further, in odd projective dimension (even vector dimension)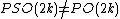
and is instead a proper (index 2) subgroup, so there is a distinct notion of orientation-preserving isometries.
For example, in n = 1 (polygons), the symmetries of a 2r-gon is the dihedral group
Dih2r (of order 4r), with rotational group the cyclic group C2r, these being subgroups of O(2) and SO(2), respectively. The projectivization of a 2r-gon (in the circle) is an r-gon (in the projective line), and accordingly the quotient groups, subgroups of PO(2) and PSO(2) are Dihr and Cr. Note that the same commutative square of subgroups occurs for the square of Spin group and Pin group
– Spin(2), Pin+(2), SO(2), O(2) – here going up to a 2-fold cover, rather than down to a 2-fold quotient.
Lastly, by the lattice theorem
there is a Galois connection
between subgroups of O(n) and subgroups of PO(n), in particular of finite subgroups. Under this connection, symmetry groups of centrally symmetric polytopes correspond to symmetry groups of the corresponding projective polytope, while symmetry groups of spherical polytopes without central symmetry correspond to symmetry groups of degree 2 projective polytopes (tilings that cover projective space twice), whose cover (corresponding to the adjunction of the connection) is a compound of two polytopes – the original polytope and its central inverse.
These symmetry groups should be compared and contrasted with binary polyhedral groups – just as Pin±(n) → O(n) is a 2-to-1 cover, and hence there is a Galois connection between binary polyhedral groups and polyhedral groups, O(n) → PO(n) is a 2-to-1-cover, and hence has an analogous Galois connection between subgroups. However, while discrete subgroups of O(n) and PO(n) correspond to symmetry groups of spherical and projective polytopes, corresponding geometrically to the covering map
there is no covering space of 
(for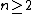 
) as the sphere is simply connected, and thus there is no corresponding "binary polytope" for which subgroups of Pin are symmetry groups.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a (globally) projective polyhedron is a tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
of the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
. These are projective analogs of spherical polyhedra – tessellations of the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
– and toroidal polyhedra – tessellations of the toroids.
Projective polyhedra are also referred to as elliptic tessellations or elliptic tilings, referring to the projective plane as (projective) elliptic geometry
Elliptic geometry
Elliptic geometry is a non-Euclidean geometry, in which, given a line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which can be interpreted as asserting that there is exactly one...
, by analogy with spherical tiling, a synonym for "spherical polyhedron". However, the term elliptic geometry
Elliptic geometry
Elliptic geometry is a non-Euclidean geometry, in which, given a line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which can be interpreted as asserting that there is exactly one...
applies to both spherical and projective geometries, so the term carries some ambiguity for polyhedra.
As cellular decomposition
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
s of the projective plane, they have Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
1, while spherical polyhedra have Euler characteristic 2. The qualifier "globally" is to contrast with locally projective polyhedra, which are defined in the theory of abstract polyhedra.
Non-overlapping projective polyhedra (density
Polytope density
In geometry, polytope density represents the number of windings of a polytope, particularly a uniform or regular polytope, around its center. It can be visually determined by counting the minimum number of facet crossings of a ray from the center to infinity...
1) correspond to spherical polyhedra (equivalently, convex polyhedra) with central symmetry. This is elaborated and extended below in relation with spherical polyhedra and relation with traditional polyhedra.
Examples
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s:
- Hemi-cube
- Hemi-octahedronHemi-octahedronA hemi-octahedron is an abstract regular polyhedron, containing half the faces of a regular octahedron.It has 4 triangular faces, 6 edges, and 3 vertices...
- Hemi-dodecahedronHemi-dodecahedronA hemi-dodecahedron is an abstract regular polyhedron, containing half the faces of a regular dodecahedron. It can be realized as a projective polyhedron , which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and...
- Hemi-icosahedronHemi-icosahedronA hemi-icosahedron is an abstract regular polyhedron, containing half the faces of a regular icosahedron. It can be realized as a projective polyhedron , which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing...
These can be obtained by taking the quotient of the associated spherical polyhedron by the antipodal map (identifying opposite points on the sphere).
On the other hand, the tetrahedron does not have central symmetry, so there is no "hemi-tetrahedron". See relation with spherical polyhedra below on how the tetrahedron is treated.
Hemipolyhedra
Note that the prefix "hemi-" is also used to refer to hemipolyhedra, which are uniform polyhedra having some faces that pass through the center of symmetry. As these do not define spherical polyhedra (because they pass through the center, which does not map to a defined point on the sphere), they do not define projective polyhedra by the quotient map from 3-space (minus the origin) to the projective plane.
Of these uniform hemipolyhedra, only the tetrahemihexahedron
Tetrahemihexahedron
In geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 6 vertices and 12 edges, and 7 faces: 4 triangular and 3 square. Its vertex figure is a crossed quadrilateral. It has Coxeter-Dynkin diagram of ....
is topologically a projective polyhedron, as can be verified by its Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
and visually obvious connection to the Roman surface
Roman surface
The Roman surface is a self-intersecting mapping of the real projective plane into three-dimensional space, with an unusually high degree of symmetry...
. It is 2-covered by the cuboctahedron
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
, and can be realized as the quotient of the spherical cuboctahedron by the antipodal map. It is the only uniform (traditional) polyhedron that is projective – that is, the only uniform projective polyhedron that immerses in Euclidean three-space as a uniform traditional polyhedron.
Relation with spherical polyhedra
There is a 2-to-1 covering mapCovering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
of the sphere to the projective plane, and under this map, projective polyhedra correspond to spherical polyhedra with central symmetry – the 2-fold cover of a projective polyhedron is a centrally symmetric spherical polyhedron. Further, because a covering mapCovering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
is a local homeomorphism
Local homeomorphism
In mathematics, more specifically topology, a local homeomorphism is intuitively a function, f, between topological spaces that preserves local structure. Equivalently, one can cover the domain of this function by open sets, such that f restricted to each such open set is a homeomorphism onto its...
(in this case a local isometry), both the spherical and the corresponding projective polyhedra have the same abstract vertex figure.
For example, the 2-fold cover of the (projective) hemi-cube is the (spherical) cube. The hemi-cube has 4 vertices, 3 faces, and 6 edges, each of which is covered by 2 copies in the sphere, and accordingly the cube has 8 vertices, 6 faces, and 12 edges, while both these polyhedra have a 4.4.4 vertex figure (3 squares meeting at a vertex).
Further, the symmetry group (of isometries) of a projective polyhedron and covering spherical polyhedron are related: the symmetries of the projective polyhedron are naturally identified with the rotation symmetries of the spherical polyhedron, while the full symmetry group of the spherical polyhedron is the product of its rotation group (the symmetry group of the projective polyhedron) and the cyclic group of order 2, {±I}. See symmetry group below for elaboration and other dimensions.
Spherical polyhedra without central symmetry do not define a projective polyhedron, as the images of vertices, edges, and faces will overlap. In the language of tilings, the image in the projective plane is a degree 2 tiling, meaning that it covers the projective plane twice – rather than 2 faces in the sphere corresponding to 1 face in the projective plane, covering it twice, each face in the sphere corresponds to a single face in the projective plane, accordingly covering it twice.
The correspondence between projective polyhedra and centrally symmetric spherical polyhedra can be extended to a Galois connection
Galois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
including all spherical polyhedra (not necessarily centrally symmetric) if the classes are extended to include degree 2 tilings of the projective plane, whose covers are not polyhedra but rather the polyhedral compound
Polyhedral compound
A polyhedral compound is a polyhedron that is itself composed of several other polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram....
of a non-centrally symmetric polyhedron, together with its central inverse (a compound of 2 polyhedra). This geometrizes the Galois connection at the level of finite subgroups of O(3) and PO(3), under which the adjunction is "union with central inverse". For example, the tetrahedron is not centrally symmetric, and has 4 vertices, 6 edges, and 4 faces, and vertex figure 3.3.3 (3 triangles meeting at each vertex). Its image in the projective plane has 4 vertices, 6 edges (which intersect), and 4 faces (which overlap), covering the projective plane twice. The cover of this is the stellated octahedron – equivalently, the compound of two tetrahedra – which has 8 vertices, 12 edges, and 8 faces, and vertex figure 3.3.3.
Generalizations
In the context of abstract polytopeAbstract polytope
In mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...
s, one instead refers to "locally projective polytopes" – see Abstract polytope: Local topology. For example, the 11-cell
11-cell
In mathematics, the 11-cell is a self-dual abstract regular 4-polytope . Its 11 cells are hemi-icosahedral. It has 11 vertices, 55 edges and 55 faces. Its symmetry group is the projective special linear group L2, so it has660 symmetries...
is a "locally projective polytope", but is not a globally projective polyhedron, nor indeed tessellates any manifold, as it not locally Euclidean, but rather locally projective, as the name indicates.
Projective polytopes can be defined in higher dimension as tessellations of projective space in one less dimension. Defining k-dimensional projective polytopes in n-dimensional projective space is somewhat trickier, because the usual definition of polytopes in Euclidean space requires taking convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
s of points, which is not a projective concept, and is infrequently addressed in the literature, but has been defined, such as in .
Symmetry group
The symmetry group of a projective polytope is a finite (hence discrete)Since PO is compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, finite and discrete sets are identical – infinite sets have an accumulation point. subgroup of the projective orthogonal group
Projective orthogonal group
In projective geometry and linear algebra, the projective orthogonal group PO is the induced action of the orthogonal group of a quadratic space V = A quadratic space is a vector space V together with a quadratic form Q; the Q is dropped from notation when it is clear. on the associated projective...
, PO, and conversely every finite subgroup of PO is the symmetry group of a projective polytope by taking the polytope given by images of a fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
for the group.
The relevant dimensions are as follows: n-dimensional real projective space is the projectivization of (n+1)-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
,
so the projective orthogonal group of an n-dimensional projective space is denoted
- PO(n+1) = P(O(n+1)) = O(n+1)/{±I}.
If n=2k is even (so n+1 = 2k+1 is odd), then O(2k+1) = SO(2k+1)×{±I} decomposes as a product, and thus
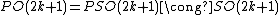The isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
/equality distinction in this equation is because the context is the 2-to-1 quotient map
– PSO(2k+1) and PO(2k+1) are equal subsets of the target (namely, the whole space), hence the equality, while the induced map 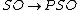is an isomorphism but the two groups are subsets of different spaces, hence the isomorphism rather than an equality.See for an example of this distinction being made. so the group of projective isometries can be identified with the group of rotational isometries.
Thus in particular the symmetry group of a projective polyhedron is the rotational symmetry group of the covering spherical polyhedron; the full symmetry group of the spherical polyhedron is then just the direct product with reflection through the origin, which is the kernel on passage to projective space. The projective plane is non-orientable, and thus there is no distinct notion of "orientation-preserving isometries of a projective polyhedron", which is reflected in the equality PSO(3) = PO(3).
If n=2k + 1 is odd, then O(n+1) = O(2k+2) does not decompose as a product, and thus the symmetry group of the projective polytope is not simply the rotational symmetries of the spherical polytope, but rather a 2-to-1 quotient of the full symmetry group of the corresponding spherical polytope (the spherical group is a central extension
Central extension
Central extension may refer to:* Central Extension , a rail line* Central extension , a type of group extension...
of the projective group). Further, in odd projective dimension (even vector dimension)
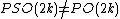and is instead a proper (index 2) subgroup, so there is a distinct notion of orientation-preserving isometries.For example, in n = 1 (polygons), the symmetries of a 2r-gon is the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
Dih2r (of order 4r), with rotational group the cyclic group C2r, these being subgroups of O(2) and SO(2), respectively. The projectivization of a 2r-gon (in the circle) is an r-gon (in the projective line), and accordingly the quotient groups, subgroups of PO(2) and PSO(2) are Dihr and Cr. Note that the same commutative square of subgroups occurs for the square of Spin group and Pin group
Pin group
In mathematics, the pin group is a certain subgroup of the Clifford algebra associated to a quadratic space. It maps 2-to-1 to the orthogonal group, just as the spin group maps 2-to-1 to the special orthogonal group....
– Spin(2), Pin+(2), SO(2), O(2) – here going up to a 2-fold cover, rather than down to a 2-fold quotient.
Lastly, by the lattice theorem
Lattice theorem
In mathematics, the lattice theorem, sometimes referred to as the fourth isomorphism theorem or the correspondence theorem, states that if N is a normal subgroup of a group G, then there exists a bijection from the set of all subgroups A of G such that A contains N, onto the set of all subgroups...
there is a Galois connection
Galois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
between subgroups of O(n) and subgroups of PO(n), in particular of finite subgroups. Under this connection, symmetry groups of centrally symmetric polytopes correspond to symmetry groups of the corresponding projective polytope, while symmetry groups of spherical polytopes without central symmetry correspond to symmetry groups of degree 2 projective polytopes (tilings that cover projective space twice), whose cover (corresponding to the adjunction of the connection) is a compound of two polytopes – the original polytope and its central inverse.
These symmetry groups should be compared and contrasted with binary polyhedral groups – just as Pin±(n) → O(n) is a 2-to-1 cover, and hence there is a Galois connection between binary polyhedral groups and polyhedral groups, O(n) → PO(n) is a 2-to-1-cover, and hence has an analogous Galois connection between subgroups. However, while discrete subgroups of O(n) and PO(n) correspond to symmetry groups of spherical and projective polytopes, corresponding geometrically to the covering map
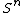there is no covering space of (for 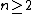) as the sphere is simply connected, and thus there is no corresponding "binary polytope" for which subgroups of Pin are symmetry groups.