Local homeomorphism
Encyclopedia
In mathematics
, more specifically topology
, a local homeomorphism is intuitively a function
, f, between topological space
s that preserves local structure. Equivalently, one can cover the domain of this function by open set
s, such that f restricted to each such open set is a homeomorphism
onto its image. In particular, every homeomorphism
is a local homeomorphism. The formal definition is given below.
Local homeomorphisms are very important in mathematics, particularly in the theory of manifold
s (e.g. differential topology
) and algebraic topology
. An important example of local homeomorphisms are covering map
s. Covering maps are important, because unlike local homeomorphisms, they satisfy the local triviality condition, they induce isomorphisms
of particular homotopy group
s, and in particular, one can lift any path
in the base space of a covering map, to a path in the total space. Although local homeomorphisms are not as strong as covering maps in this respect, they have many important applications in differential topology
; namely one uses the notion of a local homeomorphism to define a differentiable manifold
.
s. A function
,
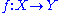is a local homeomorphism, if for every point x in X, there exists an open set U containing x, such that 
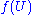is open in Y and 
is a homeomorphism
.
Let f : S1 → S1 be the map that wraps the circle
around itself n times (i.e. has winding number
n). This is a local homeomorphism for all non-zero n, but a homeomorphism only in the cases where it is bijective, i.e. n = 1 or -1.
It is shown in complex analysis
that a complex analytic function f gives a local homeomorphism precisely when the derivative
f′(z) is non-zero for all z in the domain of f. The function f(z) = zn on an open disk around 0 is not a local homeomorphism at 0 when n is at least 2. In that case 0 is a point of "ramification
" (intuitively, n sheets come together there).
A local homeomorphism f : X → Y preserves "local" topological properties:
If f : X → Y is a local homeomorphism and U is an open subset of X, then the restriction f|U is also a local homeomorphism.
If f : X → Y and g : Y → Z are local homeomorphisms, then the composition gf : X → Z is also a local homeomorphism.
The local homeomorphisms with codomain
Y stand in a natural 1-1 correspondence with the sheaves
of sets on Y. Furthermore, every continuous map with codomain Y gives rise to a uniquely defined local homeomorphism with codomain Y in a natural way. All of this is explained in detail in the article on sheaves
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a local homeomorphism is intuitively a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, f, between topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s that preserves local structure. Equivalently, one can cover the domain of this function by open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s, such that f restricted to each such open set is a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
onto its image. In particular, every homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
is a local homeomorphism. The formal definition is given below.
Local homeomorphisms are very important in mathematics, particularly in the theory of manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s (e.g. differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
) and algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
. An important example of local homeomorphisms are covering map
Covering map
In mathematics, more specifically algebraic topology, a covering map is a continuous surjective function p from a topological space, C, to a topological space, X, such that each point in X has a neighbourhood evenly covered by p...
s. Covering maps are important, because unlike local homeomorphisms, they satisfy the local triviality condition, they induce isomorphisms
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
of particular homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s, and in particular, one can lift any path
Path
Path, pathway or PATH may refer to:-Path:* Course , the intended path of a vehicle over the surface of the Earth* Trail, hiking trail, footpath, or bridle path...
in the base space of a covering map, to a path in the total space. Although local homeomorphisms are not as strong as covering maps in this respect, they have many important applications in differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
; namely one uses the notion of a local homeomorphism to define a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
.
Formal definition
Let X and Y be topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s. A function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
,
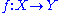is a local homeomorphism, if for every point x in X, there exists an open set U containing x, such that 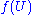is open in Y and is a homeomorphismHomeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
.
Examples
If U is an open subset of Y equipped with the subspace topology, then the inclusion map i : U → Y is a local homeomorphism. Openness is essential here: the inclusion map of a non-open subset of Y never yields a local homeomorphism.Let f : S1 → S1 be the map that wraps the circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
around itself n times (i.e. has winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
n). This is a local homeomorphism for all non-zero n, but a homeomorphism only in the cases where it is bijective, i.e. n = 1 or -1.
It is shown in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
that a complex analytic function f gives a local homeomorphism precisely when the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
f′(z) is non-zero for all z in the domain of f. The function f(z) = zn on an open disk around 0 is not a local homeomorphism at 0 when n is at least 2. In that case 0 is a point of "ramification
Ramification
In mathematics, ramification is a geometric term used for 'branching out', in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign...
" (intuitively, n sheets come together there).
Properties
Every local homeomorphism is a continuous and open map. A bijective local homeomorphism is therefore a homeomorphism.A local homeomorphism f : X → Y preserves "local" topological properties:
- X is locally connectedLocally connected spaceIn topology and other branches of mathematics, a topological space X islocally connected if every point admits a neighbourhood basis consisting entirely of open, connected sets.-Background:...
if and only if f(X) is - X is locally path-connectedLocally connected spaceIn topology and other branches of mathematics, a topological space X islocally connected if every point admits a neighbourhood basis consisting entirely of open, connected sets.-Background:...
if and only if f(X) is - X is locally compact if and only if f(X) is
- X is first-countableFirst-countable spaceIn topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X is said to be first-countable if each point has a countable neighbourhood basis...
if and only if f(X) is
If f : X → Y is a local homeomorphism and U is an open subset of X, then the restriction f|U is also a local homeomorphism.
If f : X → Y and g : Y → Z are local homeomorphisms, then the composition gf : X → Z is also a local homeomorphism.
The local homeomorphisms with codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
Y stand in a natural 1-1 correspondence with the sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of sets on Y. Furthermore, every continuous map with codomain Y gives rise to a uniquely defined local homeomorphism with codomain Y in a natural way. All of this is explained in detail in the article on sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
.