
Octahemioctahedron
Encyclopedia
In geometry
, the octahemioctahedron is a nonconvex uniform polyhedron
, indexed as U3. Its vertex figure
is a crossed quadrilateral
.
It is one of nine hemipolyhedra
with 4 hexagonal faces passing through the model center.
and edge arrangement with the cuboctahedron
(having the triangular faces in common), and with the cubohemioctahedron
(having the hexagonal faces in common).
By construction it has tetrahedral symmetry
(Td), like the cantellated tetrahedron construction for the cuboctahedron,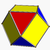 , with alternate triangles with inverted orientations. Without alternating triangles, it has octahedral symmetry
, with alternate triangles with inverted orientations. Without alternating triangles, it has octahedral symmetry
(Oh).
of zero (a topological torus
).
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the octahemioctahedron is a nonconvex uniform polyhedron
Nonconvex uniform polyhedron
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting...
, indexed as U3. Its vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
is a crossed quadrilateral
Antiparallelogram
An antiparallelogram is a quadrilateral in which, like a parallelogram, the pairs of nonadjacent sides are congruent, but in which two opposite sides intersect and are therefore not parallel.-Properties:Every antiparallelogram has an axis of symmetry through its crossing point...
.
It is one of nine hemipolyhedra
Hemipolyhedron
In geometry, a hemipolyhedron is a uniform star polyhedron some of whose faces pass through its center. These "hemi" faces lie parallel to the faces of some other symmetrical polyhedron, and their count is half the number of faces of that other polyhedron - hence the "hemi" prefix.The prefix "hemi"...
with 4 hexagonal faces passing through the model center.
Related polyhedra
It shares the vertex arrangementVertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
and edge arrangement with the cuboctahedron
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
(having the triangular faces in common), and with the cubohemioctahedron
Cubohemioctahedron
In geometry, the cubohemioctahedron is a nonconvex uniform polyhedron, indexed as U15. Its vertex figure is a crossed quadrilateral.A nonconvex polyhedron has intersecting faces which do not represent new edges or faces...
(having the hexagonal faces in common).
 Cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
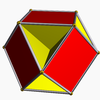 Cubohemioctahedron Cubohemioctahedron In geometry, the cubohemioctahedron is a nonconvex uniform polyhedron, indexed as U15. Its vertex figure is a crossed quadrilateral.A nonconvex polyhedron has intersecting faces which do not represent new edges or faces... |
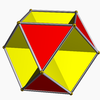 Octahemioctahedron |
By construction it has tetrahedral symmetry
Tetrahedral symmetry
150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
(Td), like the cantellated tetrahedron construction for the cuboctahedron,
 , with alternate triangles with inverted orientations. Without alternating triangles, it has octahedral symmetry
, with alternate triangles with inverted orientations. Without alternating triangles, it has octahedral symmetryOctahedral symmetry
150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...
(Oh).
Orientability
It is the only hemipolyhedron that is orientable, and the only uniform polyhedron with an Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of zero (a topological torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
).
The topological net of faces can be arranged as a rhombus Rhombus In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every... divided into 8 triangles and 4 hexagons. All vertex angle defects are zero. |

