
Hemipolyhedron
Encyclopedia
In geometry
, a hemipolyhedron is a uniform star polyhedron some of whose faces pass through its center. These "hemi" faces lie parallel to the faces of some other symmetrical polyhedron, and their count is half the number of faces of that other polyhedron - hence the "hemi" prefix.
The prefix "hemi" is also used to refer to projective polyhedra, such as the hemi-cube, which are the image of a 2 to 1 map of a spherical polyhedron
with central symmetry.
s are of the form p/(p − 1) p | r; their vertex figure
s are crossed quadrilaterals. The vertex configuration
is p·2r·p/(p − 1)·2r. The 2r-gon faces pass through the center of the model. The p/(p − 1) notation implies a convex p-gonal faces turning backwards around the vertex figure. Pentagrams that turn backwards around the vertex figure use a 5/3 notation, while decagrams use a 10/7 notation.
The nine forms, listed with their vertex figure
s are:
passing through the center, the dual figures
have some vertices
at infinity; properly, on the real projective plane
at infinity, since one wishes to count only one vertex for each pair of prisms going in opposite directions. In Magnus Wenninger
's Dual Models, they are represented with intersecting infinite prisms
passing through the model center, cut off at a certain point that is convenient for the maker. Wenninger suggested these figures are members of a new class of stellation
figures, called stellation to infinity. However, he also acknowledged that strictly speaking they are not polyhedra because their construction does not conform to the usual definitions.
There are 9 such duals, sharing only 5 distinct outward forms, four of them existing in identical pairs. The members of a given pair differ in their arrangements of true vertices vs. points where edges pass through each other. The outwards forms are:
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a hemipolyhedron is a uniform star polyhedron some of whose faces pass through its center. These "hemi" faces lie parallel to the faces of some other symmetrical polyhedron, and their count is half the number of faces of that other polyhedron - hence the "hemi" prefix.
The prefix "hemi" is also used to refer to projective polyhedra, such as the hemi-cube, which are the image of a 2 to 1 map of a spherical polyhedron
Spherical polyhedron
In mathematics, a spherical polyhedron is a tiling of the sphere in which the surface is divided or partitioned by great arcs into bounded regions called spherical polygons...
with central symmetry.
Wythoff symbol and vertex figure
Their Wythoff symbolWythoff symbol
In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....
s are of the form p/(p − 1) p | r; their vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s are crossed quadrilaterals. The vertex configuration
Vertex configuration
In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...
is p·2r·p/(p − 1)·2r. The 2r-gon faces pass through the center of the model. The p/(p − 1) notation implies a convex p-gonal faces turning backwards around the vertex figure. Pentagrams that turn backwards around the vertex figure use a 5/3 notation, while decagrams use a 10/7 notation.
The nine forms, listed with their vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s are:
 Tetrahemihexahedron Tetrahemihexahedron In geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 6 vertices and 12 edges, and 7 faces: 4 triangular and 3 square. Its vertex figure is a crossed quadrilateral. It has Coxeter-Dynkin diagram of .... (3.4.3/2.4) (p = 3, r = 2) |
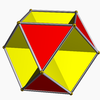 Octahemioctahedron Octahemioctahedron In geometry, the octahemioctahedron is a nonconvex uniform polyhedron, indexed as U3. Its vertex figure is a crossed quadrilateral.It is one of nine hemipolyhedra with 4 hexagonal faces passing through the model center.- Related polyhedra :... (3.6.3/2.6) (p = 3, r = 3) |
 Small icosihemidodecahedron Small icosihemidodecahedron In geometry, the small icosihemidodecahedron is a uniform star polyhedron, indexed as U49. Its vertex figure alternates two regular triangles and decagons as a crossed quadrilateral.... (3.10.3/2.10) (p = 3, r = 5) |
 Great icosihemidodecahedron Great icosihemidodecahedron In geometry, the great icosihemidodecahedron is a nonconvex uniform polyhedron, indexed as U71. Its vertex figure is a crossed quadrilateral.It is a hemipolyhedron with 6 decagrammic faces passing through the model center.- Related polyhedra :... (10/3.3.10/7.3) (p = 3, r = 5/3) |
 Small dodecahemicosahedron Small dodecahemicosahedron In geometry, the small dodecahemicosahedron is a nonconvex uniform polyhedron, indexed as U62. Its vertex figure is a crossed quadrilateral.It is a hemipolyhedron with ten hexagonal faces passing through the model center.- Related polyhedra :... (5/2.6.5/3.6) (p = 5/2, r = 3) |
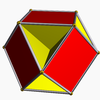 Cubohemioctahedron Cubohemioctahedron In geometry, the cubohemioctahedron is a nonconvex uniform polyhedron, indexed as U15. Its vertex figure is a crossed quadrilateral.A nonconvex polyhedron has intersecting faces which do not represent new edges or faces... (4.6.4/3.6) (p = 4, r = 3) |
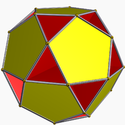 Small dodecahemidodecahedron Small dodecahemidodecahedron In geometry, the small dodecahemidodecahedron is a nonconvex uniform polyhedron, indexed as U51. Its vertex figure alternates two regular pentagons and decagons as a crossed quadrilateral.... (5.10.5/4.10) (p = 5, r = 5) |
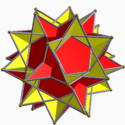 Great dodecahemidodecahedron Great dodecahemidodecahedron In geometry, the great dodecahemidodecahedron is a nonconvex uniform polyhedron, indexed as U70. Its vertex figure is a crossed quadrilateral.... (5/2.10/3.5/3.10/3) (p = 5/2, r = 5/3) |
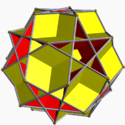 Great dodecahemicosahedron Great dodecahemicosahedron In geometry, the great dodecahemicosahedron is a nonconvex uniform polyhedron, indexed as U65. Its vertex figure is a crossed quadrilateral.It is a hemipolyhedron with ten hexagonal faces passing through the model center.- Related polyhedra :... (5.6.5/4.6) (p = 5, r = 3) |
Duals of the hemipolyhedra
Since the hemipolyhedra have facesFace (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
passing through the center, the dual figures
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
have some vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
at infinity; properly, on the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
at infinity, since one wishes to count only one vertex for each pair of prisms going in opposite directions. In Magnus Wenninger
Magnus Wenninger
Father Magnus J. Wenninger OSB is a mathematician who works on constructing polyhedron models, and wrote the first book on their construction.-Early life and education:...
's Dual Models, they are represented with intersecting infinite prisms
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
passing through the model center, cut off at a certain point that is convenient for the maker. Wenninger suggested these figures are members of a new class of stellation
Stellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
figures, called stellation to infinity. However, he also acknowledged that strictly speaking they are not polyhedra because their construction does not conform to the usual definitions.
There are 9 such duals, sharing only 5 distinct outward forms, four of them existing in identical pairs. The members of a given pair differ in their arrangements of true vertices vs. points where edges pass through each other. The outwards forms are:
| Tetrahemihexacron Tetrahemihexacron In geometry, the tetrahemihexacron is the dual of the tetrahemihexahedron, and is one of nine dual hemipolyhedra.Since the tetrahemihexahedron has three square faces passing through the model centre, the tetrahemihexacron has three vertices at infinity... |
Octahemioctacron Octahemioctacron In geometry, the octahemioctacron is the dual of the octahemioctahedron, and is one of nine dual hemipolyhedra. It appears visually indistinct from the hexahemioctacron.... and hexahemioctacron Hexahemioctacron In geometry, the hexahemioctacron is the dual of the cubohemioctahedron, and is one of nine dual hemipolyhedra. It appears visually indistinct from the octahemioctacron.... |
Small icosihemidodecacron Small icosihemidodecacron In geometry, the small icosihemidodecacron is the dual of the small icosihemidodecahedron, and is one of nine dual hemipolyhedra. It appears visually indistinct from the small dodecahemidodecacron.... and small dodecahemidodecacron Small dodecahemidodecacron In geometry, the small dodecahemidodecacron is the dual of the small dodecahemidodecahedron, and is one of nine dual hemipolyhedra. It appears visually indistinct from the small icosihemidodecacron.... |
Great dodecahemidodecacron Great dodecahemidodecacron In geometry, the great dodecahemidodecacron is the dual of the great dodecahemidodecahedron, and is one of nine dual hemipolyhedra. It is appears indistinct from the great icosihemidodecacron.... and great icosihemidodecacron Great icosihemidodecacron In geometry, the great icosihemidodecacron is the dual of the great icosihemidodecahedron, and is one of nine dual hemipolyhedra. It appears indistinct from the great dodecahemidodecacron.... |
Great dodecahemicosacron Great dodecahemicosacron In geometry, the great dodecahemicosacron is the dual of the great dodecahemicosahedron, and is one of nine dual hemipolyhedra. It appears visually indistinct from the small dodecahemicosacron.... and small dodecahemicosacron Small dodecahemicosacron In geometry, the small dodecahemicosacron is the dual of the small dodecahemicosahedron, and is one of nine dual hemipolyhedra. It appears visually indistinct from the great dodecahemicosacron.... |
| 3 intersecting infinite square prisms | 4 intersecting infinite hexagonal prisms | 6 intersecting infinite decagonal prisms | 6 intersecting infinite decagrammic prisms | 10 intersecting infinite hexagonal prisms |

