Spherical trigonometry is a branch of
spherical geometrySpherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
which deals with
polygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
s (especially
triangleA triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s) on the
sphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
and the relationships between the sides and the
angleIn geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s. This is of great importance for calculations in
astronomyAstronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
and earth-surface, orbital and space
navigationNavigation is the process of monitoring and controlling the movement of a craft or vehicle from one place to another. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks...
.
History
Spherical triangles were studied by early
Greek mathematiciansGreek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
such as
Menelaus of AlexandriaMenelaus of Alexandria was a Greek mathematician and astronomer, the first to recognize geodesics on a curved surface as natural analogs of straight lines.-Life and Works:...
, who wrote a book on spherical triangles called
Sphaerica and developed
Menelaus' theoremMenelaus' theorem, named for Menelaus of Alexandria, is a theorem about triangles in plane geometry. Given a triangle ABC, and a transversal line that crosses BC, AC and AB at points D, E and F respectively, with D, E, and F distinct from A, B and C, thenThis equation uses signed lengths of...
. E. S. Kennedy, however, points out that while it was possible in ancient mathematics to compute the magnitudes of a spherical figure, in principle, by use of the table of
chordsA chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
and Menelaus' theorem, the application of the theorem to spherical problems was very difficult in practice.
Islamic world
Further advances were made in the Islamic world. In order to observe holy days on the
Islamic calendarThe Hijri calendar , also known as the Muslim calendar or Islamic calendar , is a lunar calendar consisting of 12 lunar months in a year of 354 or 355 days. It is used to date events in many Muslim countries , and used by Muslims everywhere to determine the proper day on which to celebrate Islamic...
in which timings were determined by phases of the moon, the astronomers initially used Menalaus' method to calculate the place of the
moonThe Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
and
starA star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s, though this method proved to be clumsy and difficult. It involved setting up two intersecting
right triangleA right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
s; by applying Menelaus' theorem it was possible to solve one of the six sides, but only if the other five sides were known. To tell the time from the
sunThe Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
's
altitudeAltitude or height is defined based on the context in which it is used . As a general definition, altitude is a distance measurement, usually in the vertical or "up" direction, between a reference datum and a point or object. The reference datum also often varies according to the context...
, for instance, repeated applications of Menelaus' theorem were required. For medieval Islamic astronomers, there was an obvious challenge to find a simpler trigonometric method.
In the early 9th century,
Muhammad ibn Mūsā al-Khwārizmī'There is some confusion in the literature on whether al-Khwārizmī's full name is ' or '. Ibn Khaldun notes in his encyclopedic work: "The first who wrote upon this branch was Abu ʿAbdallah al-Khowarizmi, after whom came Abu Kamil Shojaʿ ibn Aslam." . 'There is some confusion in the literature on...
, a Persian Mathematician, was an early pioneer in spherical trigonometry and wrote a treatise on the subject. In the 10th century, another Persian Mathematician Abū al-Wafā' al-Būzjānī established the angle addition formulas, e.g., sin(
a +
b), and discovered the
sine formulaIn trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...
for spherical trigonometry:
Here,
a,
b, and
c are the angles at the centre of the sphere subtended by the three sides of the triangle, and
α,
β, and
γ are the angles between the sides, where angle
α is opposite the side which subtends angle
a, etc.
Al-JayyaniAbū ʿAbd Allāh Muḥammad ibn Muʿādh al-Jayyānī was a mathematician, Islamic scholar, and Qadi from Al-Andalus...
(989-1079), an
Arabic mathematicianIn the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
in
Islamic Iberian PeninsulaAl-Andalus was the Arabic name given to a nation and territorial region also commonly referred to as Moorish Iberia. The name describes parts of the Iberian Peninsula and Septimania governed by Muslims , at various times in the period between 711 and 1492, although the territorial boundaries...
, wrote what some consider the first treatise on spherical trigonometry,
circa 1060, entitled
The book of unknown arcs of a sphere, in which spherical trigonometry was brought into its modern form. Al-Jayyani's book "contains formulae for
right-angle trianglesA special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45-45-90. This is called an "angle-based" right triangle...
, the general
law of sinesIn trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...
and the solution of a spherical triangle by means of the polar
triangleA triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
". This treatise later had a "strong influence on European mathematics", and his "definition of
ratioIn mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
s as numbers" and "method of solving a spherical triangle when all sides are unknown" are likely to have influenced
RegiomontanusJohannes Müller von Königsberg , today best known by his Latin toponym Regiomontanus, was a German mathematician, astronomer, astrologer, translator and instrument maker....
.
In the 13th century, Persian mathematician
Nasīr al-Dīn al-TūsīKhawaja Muḥammad ibn Muḥammad ibn Ḥasan Ṭūsī , better known as Naṣīr al-Dīn al-Ṭūsī , was a Persian polymath and prolific writer: an astronomer, biologist, chemist, mathematician, philosopher, physician, physicist, scientist, theologian and Marja Taqleed...
was the first to treat trigonometry as a mathematical discipline independent from astronomy, and he further developed spherical trigonometry, bringing it to its present form. He listed the six distinct cases of a right-angled triangle in spherical trigonometry. In his
On the Sector Figure, he also stated the law of sines for plane and spherical triangles, and discovered the
law of tangentsIn trigonometry, the law of tangents is a statement about the relationship between the tangents of two angles of a triangle and the lengths of the opposite sides....
for spherical triangles.
Lines and angles on a sphere
On the surface of a sphere, the closest analogue to straight
linesThe notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
are
great circleA great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
s, i.e. circles whose centers coincide with the center of the sphere. For example, simplifying the shape of the
EarthEarth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
(the
geoidThe geoid is that equipotential surface which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest , and extended through the continents . According to C.F...
) to a sphere, the
meridianA meridian is an imaginary line on the Earth's surface from the North Pole to the South Pole that connects all locations along it with a given longitude. The position of a point along the meridian is given by its latitude. Each meridian is perpendicular to all circles of latitude...
s and the
equatorAn equator is the intersection of a sphere's surface with the plane perpendicular to the sphere's axis of rotation and containing the sphere's center of mass....
are great circles on its surface, while non-equatorial lines of latitude are small circles. As with a line segment in a
planeIn mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
, an
arcIn geometry, an arc is a closed segment of a differentiable curve in the two-dimensional plane; for example, a circular arc is a segment of the circumference of a circle...
of a great circle (subtending less than 180°) on a sphere is the shortest path lying on the sphere between its two
endpointsIn geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
. Great circles are special cases of the concept of a
geodesicIn mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
.
An area on the sphere bounded by arcs of
great circleA great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
s is called a
spherical polygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
. Note that, unlike the case on a plane, spherical "
bianglesIn geometry, a digon is a polygon with two sides and two vertices. It is degenerate in a Euclidean space, but may be non-degenerate in a spherical space.A digon must be regular because its two edges are the same length...
" (two-sided analogs to triangle) are possible (such as a slice cut out of an orange). Such a polygon is also called a lune.
The
sideSide was an ancient Greek city in Anatolia, in the region of Pamphylia, in what is now Antalya province, on the southern Mediterranean coast of Turkey...
s of these polygons are specified not by their lengths, but by the angles at the sphere's center subtended to the endpoints of the sides. Note that this
arc angle, measured in
radianRadian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s, when multiplied by the sphere's
radiusIn classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
equals the arc length. (In the special case of polygons on the surface of a sphere of radius one, the arc length of any side equals its subtended angle.)
Hence, a
spherical triangle is specified as usual by its corner angles and its sides, but the sides are given not by their length, but by their arc angle.
The sum of the vertex angles of spherical triangles is always larger than the sum of the angles of plane triangles, which is exactly 180°. The amount
E by which the sum of the angles exceeds 180° is called
spherical excess:
where α, β and γ denote the angles in degrees.
Girard's theorem, named after the 16th century French mathematician
Albert GirardAlbert Girard was a French-born mathematician. He studied at the University of Leiden. He "had early thoughts on the fundamental theorem of algebra" and gave the inductive definition for the Fibonacci numbers....
(earlier discovered but not published by the English mathematician
Thomas HarriotThomas Harriot was an English astronomer, mathematician, ethnographer, and translator. Some sources give his surname as Harriott or Hariot or Heriot. He is sometimes credited with the introduction of the potato to Great Britain and Ireland...
), states that this surplus determines the surface area of any spherical triangle:
where
R is the radius of the sphere. From this and the area formula for a sphere it follows that the sum of the angles of a spherical triangle is
.
The analogous result holds for
hyperbolic triangleIn mathematics, the term hyperbolic triangle has more than one meaning.-Hyperbolic geometry:In hyperbolic geometry, a hyperbolic triangle is a figure in the hyperbolic plane, analogous to a triangle in Euclidean geometry, consisting of three sides and three angles...
s, with "excess" replaced by "defect"; these are both special cases of the Gauss-Bonnet theorem.
It follows from here that there are no non-trivial similar triangles (triangles with equal angles but different side lengths and area) on a sphere. In the special case of a sphere of radius 1, the area simply equals the excess angle:
A = E. One can also use Girard's formula to obtain the discrete Gauss-Bonnet theorem.
To solve a geometric problem on the sphere, one dissects the relevant figure into
right spherical triangles (i.e.: one of the triangle's corner angles is 90°) because one can then use Napier's pentagon.
Napier's Pentagon
NapierJohn Napier of Merchiston – also signed as Neper, Nepair – named Marvellous Merchiston, was a Scottish mathematician, physicist, astronomer & astrologer, and also the 8th Laird of Merchistoun. He was the son of Sir Archibald Napier of Merchiston. John Napier is most renowned as the discoverer...
's pentagon (also known as Napier's circle) is a
mnemonic aidA mnemonic , or mnemonic device, is any learning technique that aids memory. To improve long term memory, mnemonic systems are used to make memorization easier. Commonly encountered mnemonics are often verbal, such as a very short poem or a special word used to help a person remember something,...
that helps to find all relations between the angles in a right spherical triangle.
Write the six angles of the triangle (three vertex angles, three arc angles) in the form of a circle, sticking to the order as they appear in the triangle (i.e.: start with a corner angle, write the arc angle of an attached side next to it, proceed with the next corner angle, etc. and close the circle). Then cross out the 90° corner angle and replace all angles non-adjacent to it by their complement to 90° (i.e. replace, say,
B by 90° −
B). The five numbers that you now have on your paper form Napier's Pentagon (or Napier's Circle). For any choice of three angles, one (the
middle angle) will be either adjacent to or opposite the other two angles. Then Napier's Rules hold that the
sineIn mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
of the middle angle is equal to:
- the product of the tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
s of the adjacent angles
- the product of the cosines of the opposite angles
The mnemonic for remembering the trigonometric function to use is that the first vowel of the adjective describing each angle (e.g.,
i for middle) is the first vowel of the name of the function.
As an example, starting with the angle
, we can obtain the formula:
Using the identities for complementary angles, this becomes:
See also the
Haversine formulaThe haversine formula is an equation important in navigation, giving great-circle distances between two points on a sphere from their longitudes and latitudes...
, which relates the lengths of sides and angles in spherical triangles in a numerically stable form for navigation.
Congruent triangles on a sphere
As with plane triangles, on a sphere two triangles sharing the same sequence of angle, side, angle (ASA) are necessarily congruent (that is, they have three identical sides and three identical angles). This can be seen as follows: One can situate one of the vertices with a given angle at the south pole and run the side with given length up the prime meridian. Knowing both angles at either end of the segment of fixed length ensures that the other two sides emanate with a uniquely determined trajectory, and thus will meet each other at a uniquely determined point; thus ASA is valid.
On the other hand, a like sequence of side, side, side (SSS) does not ensure congruence: For example, with side lengths of
,
and
one has a continuous family of non-congruent triangles.
Identities
Spherical triangles satisfy a spherical law of cosines
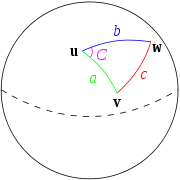
The identity may be derived by considering the triangles formed by the tangent lines to the spherical triangle subtending angle
C and using the plane law of cosines. Moreover, it reduces to the plane law in the small area limit.
They also satisfy an analogue of the
law of sinesIn trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...
And finally, they satisfy the
half-side formulaIn spherical trigonometry, the half side formula relates the angles and lengths of the sides of spherical triangles, which are triangles drawn on the surface of a sphere and so have curved sides and do not obey the formulas for plane triangles....
:
-
where
.
See also
- Air navigation
The basic principles of air navigation are identical to general navigation, which includes the process of planning, recording, and controlling the movement of a craft from one place to another....
- Spherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
- Spherical distance
The great-circle distance or orthodromic distance is the shortest distance between any two points on the surface of a sphere measured along a path on the surface of the sphere . Because spherical geometry is rather different from ordinary Euclidean geometry, the equations for distance take on a...
- Spherical polyhedron
In mathematics, a spherical polyhedron is a tiling of the sphere in which the surface is divided or partitioned by great arcs into bounded regions called spherical polygons...
- Celestial navigation
Celestial navigation, also known as astronavigation, is a position fixing technique that has evolved over several thousand years to help sailors cross oceans without having to rely on estimated calculations, or dead reckoning, to know their position...
External links