Islamic mathematics
Encyclopedia
In the history of mathematics
, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics
preserved and developed under the Islamic civilization
between circa 622 and 1600. Islamic science
and mathematics flourished under the Islamic caliphate
established across the Middle East, extending from the Iberian Peninsula
in the west to the Indus in the east and to the Almoravid Dynasty and Mali Empire
in the south.
Katz, in A History of Mathematics says that:
An important role was played by the translation and study of Greek mathematics
, which was the principal route of transmission of these texts to Western Europe. Smith notes that:
Adolph P. Yushkevich states regarding the role of Islamic mathematics:
s, but were not happy with them and only able to cope by drawing a distinction between magnitude and number. In the Greek view, magnitudes varied continuously and could be used for entities such as line segments, whereas numbers were discrete. Hence, irrationals could only be handled geometrically; and indeed Greek mathematics was mainly geometrical. Islamic mathematicians including Abū Kāmil Shujāʿ ibn Aslam slowly removed the distinction between magnitude and number, allowing irrational quantities to appear as coefficients in equations and to be solutions of algebraic equations. They worked freely with irrationals as objects, but they did not examine closely their nature.
The earliest implicit traces of mathematical induction can be found in Euclid
's proof that the number of primes is infinite
(c. 300 BCE). The first explicit formulation of the principle of induction was given by Pascal
in his Traité du triangle arithmétique (1665).
In between, implicit proof
by induction for arithmetic sequences
was introduced by al-Karaji
(c. 1000) and continued by al-Samaw'al, who used it for special cases of the binomial theorem
and properties of Pascal's triangle
.
(c. 1038/48–1123/24) wrote the Treatise on Demonstration of Problems of Algebra containing the systematic solution of third-degree equations, going beyond the Algebra of al-Khwārizmī
. Khayyám obtained the solutions of these equations by finding the intersection points of two conic section
s. This method had been used by the Greeks, but they did not generalize the method to cover all equations with positive roots.
—an approach which entailed finding the point at which a cubic polynomial obtains its maximum value. For example, in order to solve the equation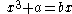
, with a and b positive, he would note that the maximum point of the curve 
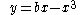occurs at 
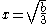, and that the equation would have no solutions, one solution or two solutions, depending on whether the height of the curve at that point was less than, equal to, or greater than 
. His surviving works give no indication of how he discovered his formulae for the maxima of these curves. Various conjectures have been proposed to account for his discovery of them.
Book chapters on Islamic mathematics |last=Berggren |first=J. Lennart |editor=Victor J. Katz |title=The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook | chapter=Mathematics in Medieval Islam | edition=Second |year=2007 |publisher=Princeton University
|location=Princeton, New Jersey |isbn=9780691114859 }}
Books on Islamic science
Books on the history of mathematics (Reviewed: )
Journal articles on Islamic mathematics
Bibliographies and biographies
Television documentaries
History of mathematics
The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past....
, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
preserved and developed under the Islamic civilization
Muslim world
The term Muslim world has several meanings. In a religious sense, it refers to those who adhere to the teachings of Islam, referred to as Muslims. In a cultural sense, it refers to Islamic civilization, inclusive of non-Muslims living in that civilization...
between circa 622 and 1600. Islamic science
Islamic science
Science in the medieval Islamic world, also known as Islamic science or Arabic science, is the science developed and practised in the Islamic world during the Islamic Golden Age . During this time, Indian, Iranian and especially Greek knowledge was translated into Arabic...
and mathematics flourished under the Islamic caliphate
Caliphate
The term caliphate, "dominion of a caliph " , refers to the first system of government established in Islam and represented the political unity of the Muslim Ummah...
established across the Middle East, extending from the Iberian Peninsula
Iberian Peninsula
The Iberian Peninsula , sometimes called Iberia, is located in the extreme southwest of Europe and includes the modern-day sovereign states of Spain, Portugal and Andorra, as well as the British Overseas Territory of Gibraltar...
in the west to the Indus in the east and to the Almoravid Dynasty and Mali Empire
Mali Empire
The Mali Empire or Mandingo Empire or Manden Kurufa was a West African empire of the Mandinka from c. 1230 to c. 1600. The empire was founded by Sundiata Keita and became renowned for the wealth of its rulers, especially Mansa Musa I...
in the south.
Katz, in A History of Mathematics says that:
"A complete history of mathematics of medieval Islam cannot yet be written, since so many of these Arabic manuscripts lie unstudied... Still, the general outline... is known. In particular, Islamic mathematicians fully developed the decimal place-value number system to include decimal fractions, systematised the study of algebra and began to consider the relationship between algebra and geometry, studied and made advances on the major Greek geometrical treatises of EuclidEuclidEuclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
, ArchimedesArchimedesArchimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
, and ApolloniusApollonius of PergaApollonius of Perga [Pergaeus] was a Greek geometer and astronomer noted for his writings on conic sections. His innovative methodology and terminology, especially in the field of conics, influenced many later scholars including Ptolemy, Francesco Maurolico, Isaac Newton, and René Descartes...
, and made significant improvements in plane and spherical geometry."
An important role was played by the translation and study of Greek mathematics
Greek mathematics
Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
, which was the principal route of transmission of these texts to Western Europe. Smith notes that:
"the world owes a great debt to Arab scholars for preserving and transmitting to posterity the classics of Greek mathematics... their work was chiefly that of transmission, although they developed considerable ingenuity in algebra and showed some genius in their work in trigonometry."
Adolph P. Yushkevich states regarding the role of Islamic mathematics:
The Islamic mathematicians exercised a prolific influence on the development of science in Europe, enriched as much by their own discoveries as those they had inherited by the Greeks, the Indians, the Syrians, the Babylonians,etc.
History
Algebra
The most important contribution of the Islamic mathematicians was the development of algebra; combining Indian and Babylonian material with the Greek geometry to develop algebra.Irrational numbers
The Greeks had discovered Irrational numberIrrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s, but were not happy with them and only able to cope by drawing a distinction between magnitude and number. In the Greek view, magnitudes varied continuously and could be used for entities such as line segments, whereas numbers were discrete. Hence, irrationals could only be handled geometrically; and indeed Greek mathematics was mainly geometrical. Islamic mathematicians including Abū Kāmil Shujāʿ ibn Aslam slowly removed the distinction between magnitude and number, allowing irrational quantities to appear as coefficients in equations and to be solutions of algebraic equations. They worked freely with irrationals as objects, but they did not examine closely their nature.
Induction
The earliest implicit traces of mathematical induction can be found in Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
's proof that the number of primes is infinite
Euclid's theorem
Euclid's theorem is a fundamental statement in number theory that asserts that there are infinitely many prime numbers. There are several well-known proofs of the theorem.-Euclid's proof:...
(c. 300 BCE). The first explicit formulation of the principle of induction was given by Pascal
Blaise Pascal
Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
in his Traité du triangle arithmétique (1665).
In between, implicit proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
by induction for arithmetic sequences
Arithmetic progression
In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
was introduced by al-Karaji
Al-Karaji
' was a 10th century Persian Muslim mathematician and engineer. His three major works are Al-Badi' fi'l-hisab , Al-Fakhri fi'l-jabr wa'l-muqabala , and Al-Kafi fi'l-hisab .Because al-Karaji's original works in Arabic are lost, it is not...
(c. 1000) and continued by al-Samaw'al, who used it for special cases of the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
and properties of Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
.
Omar Khayyám
Omar KhayyámOmar Khayyám
Omar Khayyám was aPersian polymath: philosopher, mathematician, astronomer and poet. He also wrote treatises on mechanics, geography, mineralogy, music, climatology and theology....
(c. 1038/48–1123/24) wrote the Treatise on Demonstration of Problems of Algebra containing the systematic solution of third-degree equations, going beyond the Algebra of al-Khwārizmī
Muhammad ibn Musa al-Khwarizmi
'There is some confusion in the literature on whether al-Khwārizmī's full name is ' or '. Ibn Khaldun notes in his encyclopedic work: "The first who wrote upon this branch was Abu ʿAbdallah al-Khowarizmi, after whom came Abu Kamil Shojaʿ ibn Aslam." . 'There is some confusion in the literature on...
. Khayyám obtained the solutions of these equations by finding the intersection points of two conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
s. This method had been used by the Greeks, but they did not generalize the method to cover all equations with positive roots.
Sharaf al-Dīn al-Ṭūsī
Sharaf al-Dīn al-Ṭūsī (? in Tus, Iran – 1213/4) developed a novel approach to the investigation of cubic equationsCubic function
In mathematics, a cubic function is a function of the formf=ax^3+bx^2+cx+d,\,where a is nonzero; or in other words, a polynomial of degree three. The derivative of a cubic function is a quadratic function...
—an approach which entailed finding the point at which a cubic polynomial obtains its maximum value. For example, in order to solve the equation
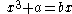, with a and b positive, he would note that the maximum point of the curve 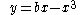occurs at 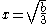, and that the equation would have no solutions, one solution or two solutions, depending on whether the height of the curve at that point was less than, equal to, or greater than . His surviving works give no indication of how he discovered his formulae for the maxima of these curves. Various conjectures have been proposed to account for his discovery of them.Other major figures
- Muhammad ibn Mūsā al-KhwārizmīMuhammad ibn Musa al-Khwarizmi'There is some confusion in the literature on whether al-Khwārizmī's full name is ' or '. Ibn Khaldun notes in his encyclopedic work: "The first who wrote upon this branch was Abu ʿAbdallah al-Khowarizmi, after whom came Abu Kamil Shojaʿ ibn Aslam." . 'There is some confusion in the literature on...
(c. 780 – c. 850) - 'Abd al-Hamīd ibn Turk'Abd al-Hamid ibn Turk' , known also as ' was a ninth century Turkic Muslim mathematician. Not much is known about his biography. The two records of him, one by Ibn Nadim and the other by al-Qifti are not identical. However al-Qifi mentions his name as ʿAbd al-Hamīd ibn Wase ibn Turk Jili...
(fl. 830) (quadratics) - Thabit ibn QurraThabit ibn Qurra' was a mathematician, physician, astronomer and translator of the Islamic Golden Age.Ibn Qurra made important discoveries in algebra, geometry and astronomy...
(826–901) - Abū Kāmil Shujā ibn Aslam (c. 850 – 930) (irrationals)
- Abū Sahl al-Qūhī (c. 940–1000) (centers of gravity)
- Abu'l-Hasan al-UqlidisiAbu'l-Hasan al-UqlidisiAbu'l Hasan Ahmad ibn Ibrahim Al-Uqlidisi was an Arab mathematician who was active in Damascus and Baghdad. As his surname indicates, he was a copyist of Euclid's works. He wrote the earliest surviving book on the positional use of the Arabic numerals, Kitab al-Fusul fi al-Hisab al-Hindi around 952...
(952 – 953) (arithmetic) - 'Abd al-'Aziz al-Qabisi
- Abū al-Wafā' Būzjānī (940 – 998) (spherical trigonometry)
- Al-KarajiAl-Karaji' was a 10th century Persian Muslim mathematician and engineer. His three major works are Al-Badi' fi'l-hisab , Al-Fakhri fi'l-jabr wa'l-muqabala , and Al-Kafi fi'l-hisab .Because al-Karaji's original works in Arabic are lost, it is not...
(c. 953 – c. 1029) (algebra, induction) - Abu Nasr MansurAbu Nasr MansurAbu Nasr Mansur ibn Ali ibn Iraq was a Persian Muslim mathematician. He is well known for his work with the spherical sine law....
(c. 960 – 1036) (spherical trigonometry) - Ibn Tahir al-BaghdadiIbn Tahir al-BaghdadiAbu Mansur Abd al-Qahir ibn Tahir ibn Muhammad ibn Abdallah al-Tamimi al-Shaffi al-Baghdadi was an Arabian mathematician from Baghdad who is best known for his treatise al-Takmila fi'l-Hisab. It contains results in number theory, and comments on works by al-Khwarizmi which are now lost.-...
(c. 980–1037) (irrationals) - Ibn al-Haytham (ca. 965–1040)
- Abū al-Rayḥān al-Bīrūnī (973 – 1048) (trigonometry)
- Al-Khayyam (1048–1131) (cubic equations, parallel postulate)
- Ibn Yaḥyā al-Maghribī al-Samawʾal (c. 1130 – c. 1180)
- Sharaf al-Dīn al-Ṭūsī (c. 1150–1215) (cubics)
- Naṣīr al-Dīn al-ṬūsīNasir al-Din al-TusiKhawaja Muḥammad ibn Muḥammad ibn Ḥasan Ṭūsī , better known as Naṣīr al-Dīn al-Ṭūsī , was a Persian polymath and prolific writer: an astronomer, biologist, chemist, mathematician, philosopher, physician, physicist, scientist, theologian and Marja Taqleed...
(1201–1274) (parallel postulate) - Jamshīd al-KāshīJamshid al-KashiGhiyāth al-Dīn Jamshīd Masʾūd al-Kāshī was a Persian astronomer and mathematician.-Biography:...
(c. 1380–1429) (decimals)
See also
- Timeline of Islamic science and technologyTimeline of Islamic science and technologyThis timeline of science and engineering in the Islamic world covers the time period from the 7th century AD to the introduction of European science to the Islamic world in the 19th and 20th centuries...
- Islamic Golden AgeIslamic Golden AgeDuring the Islamic Golden Age philosophers, scientists and engineers of the Islamic world contributed enormously to technology and culture, both by preserving earlier traditions and by adding their own inventions and innovations...
- Hindu and Buddhist contribution to science in medieval Islam
Further reading
Books on Islamic mathematics-
- Review:
- Review: ) Sowjetische Beiträge zur Geschichte der Naturwissenschaft pp. 62–160.
Book chapters on Islamic mathematics |last=Berggren |first=J. Lennart |editor=Victor J. Katz |title=The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook | chapter=Mathematics in Medieval Islam | edition=Second |year=2007 |publisher=Princeton University
Princeton University Press
-Further reading:* "". Artforum International, 2005.-External links:* * * * *...
|location=Princeton, New Jersey |isbn=9780691114859 }}
Books on Islamic science
Books on the history of mathematics (Reviewed: )
Journal articles on Islamic mathematics
- Høyrup, Jens. “The Formation of «Islamic Mathematics»: Sources and Conditions”. Filosofi og Videnskabsteori på Roskilde Universitetscenter. 3. Række: Preprints og Reprints 1987 Nr. 1.
Bibliographies and biographies
- Brockelmann, CarlCarl BrockelmannCarl Brockelmann , German Semiticist, was the foremost orientalist of his generation. He was a professor at the universities in Breslau, Berlin and, from 1903, Königsberg...
. Geschichte der Arabischen Litteratur. 1.–2. Band, 1.–3. Supplementband. Berlin: Emil Fischer, 1898, 1902; Leiden: Brill, 1937, 1938, 1942.
Television documentaries
- Marcus du SautoyMarcus du SautoyMarcus Peter Francis du Sautoy OBE is the Simonyi Professor for the Public Understanding of Science and a Professor of Mathematics at the University of Oxford. Formerly a Fellow of All Souls College, and Wadham College, he is now a Fellow of New College...
(presenter) (2008). "The Genius of the East". The Story of MathsThe Story of MathsThe Story of Maths is a British television series outlining aspects of the history of mathematics. The series was a co-production between the Open University and the BBC and aired in October 2008 on BBC Four. The material was written and presented by Oxford professor Marcus du Sautoy...
. BBCBBCThe British Broadcasting Corporation is a British public service broadcaster. Its headquarters is at Broadcasting House in the City of Westminster, London. It is the largest broadcaster in the world, with about 23,000 staff...
. - Jim Al-KhaliliJim Al-KhaliliJim Al-Khalili OBE is an Iraqi-born British theoretical physicist, author and science communicator. He is Professor of Theoretical Physics and Chair in the Public Engagement in Science at the University of Surrey...
(presenter) (2010). Science and IslamScience and Islam (documentary)Science and Islam is a three-part BBC documentary about the history of science in medieval Islamic civilization presented by Jim Al-Khalili...
. BBCBBCThe British Broadcasting Corporation is a British public service broadcaster. Its headquarters is at Broadcasting House in the City of Westminster, London. It is the largest broadcaster in the world, with about 23,000 staff...
.