
Omar Khayyám
Encyclopedia
Omar Khayyám
was a
Persian polymath
: philosopher, mathematician
, astronomer
and poet
. He also wrote treatises on mechanics
, geography
, mineralogy
, music
, climatology
and theology
.
Born in Nishapur
, at a young age he moved to Samarkand
and obtained his education there, afterwards he moved to Bukhara
and became established as one of the major mathematicians and astronomers of the medieval period. He is the author of one of the most important treatises on algebra
written before modern times, the Treatise on Demonstration of Problems of Algebra, which includes a geometric method for solving cubic equations by intersecting a hyperbola
with a circle
. He contributed to a calendar reform
.
His significance as a philosopher and teacher, and his few remaining philosophical works, have not received the same attention as his scientific and poetic writings. Zamakhshari referred to him as “the philosopher of the world”. Many sources have testified that he taught for decades the philosophy of Ibn Sina in Nishapur
where Khayyám was born and buried and where his mausoleum today remains a masterpiece of Iranian architecture
visited by many people every year.
Outside Iran and Persian speaking countries, Khayyám has had an impact on literature and societies through the translation of his works and popularization by other scholars. The greatest such impact was in English-speaking countries; the English scholar Thomas Hyde
(1636–1703) was the first non-Persian to study him. The most influential of all was Edward FitzGerald
(1809–83), who made Khayyám the most famous poet of the East in the West through his celebrated translation and adaptations of Khayyám's rather small number of quatrain
s (rubaiyaas) in Rubáiyát of Omar Khayyám
.
,(modern-day Iran
), then a Seljuq
capital in Khorasan
, which rivaled Cairo
or Baghdad
in cultural prominence in that era. He is thought to have been born into a family of tent makers (khayyami, lit. in Farsi "tent-maker"), which he would make this into a play on words later in life:
He spent part of his childhood in the town of Balkh
(present northern Afghanistan
), studying under the well-known scholar Sheikh Muhammad Mansuri. He later studied under Imam
Mowaffaq Nishapuri, who was considered one of the greatest teachers of the Khorasan
region. Throughout his life Omar Khayyám was dedicated to his efforts and abilities, in the day he would teach Algebra
and Geometry
in the evening he would attend the Seljuq court as an adviser of Malik-Shah I and at night he would study Astronomy
and complete the important aspects of the Jalali calendar.
Omar Khayyám's years in Isfahan were very productive ones but after the death of the Seljuq Sultan
Malik-Shah I (presumably by the Assassins sect), the Sultan's widow turned against him as an adviser and and soon therefore Omar Khayyám set out on his Hajj
or Pilgrimage to Mecca
and Medina
. He was then allowed to work as a court astrologer and was permitted to return to Nishapur
where he was famous for works and continued to teach mathematics, astronomy and even medicine.
. He wrote the influential Treatise on Demonstration of Problems of Algebra (1070), which laid down the principles of algebra
, part of the body of Persian Mathematics that was eventually transmitted to Europe. In particular, he derived general methods for solving cubic equations and even some higher orders.
 In the Treatise he wrote on the triangular array
In the Treatise he wrote on the triangular array
of binomial coefficient
s known as Pascal's triangle
. In 1077, Khayyám wrote Sharh ma ashkala min musadarat kitab Uqlidis (Explanations of the Difficulties in the Postulates of Euclid) published in English as "On the Difficulties of Euclid
's Definitions". An important part of the book is concerned with Euclid's famous parallel postulate, which attracted the interest of Thabit ibn Qurra
. Al-Haytham had previously attempted a demonstration of the postulate; Khayyám's attempt was a distinct advance, and his criticisms made their way to Europe, and may have contributed to the eventual development of non-Euclidean geometry
.
Omar Khayyám had notable works in geometry
, specifically on the theory of proportions, his notable contemporary mathematicians included Al-Khazini
and Abu Hatim al-Muzaffar ibn Ismail al-Isfizari
 Khayyám wrote a book entitled Explanations of the difficulties in the postulates in Euclid's Elements. The book consists of several sections on the parallel postulate (Book I), on the Euclidean definition of ratios and the Anthyphairetic ratio (modern continued fractions) (Book II), and on the multiplication of ratios (Book III).
Khayyám wrote a book entitled Explanations of the difficulties in the postulates in Euclid's Elements. The book consists of several sections on the parallel postulate (Book I), on the Euclidean definition of ratios and the Anthyphairetic ratio (modern continued fractions) (Book II), and on the multiplication of ratios (Book III).
The first section is a treatise containing some propositions and lemmas concerning the parallel postulate. It has reached the Western world from a reproduction in a manuscript written in 1387-88 AD by the Persian mathematician Tusi. Tusi mentions explicitly that he re-writes the treatise "in Khayyám's own words" and quotes Khayyám, saying that "they are worth adding to Euclid's Elements (first book) after Proposition 28." This proposition states a condition enough for having two lines in plane parallel to one another. After this proposition follows another, numbered 29, which is converse to the previous one. The proof of Euclid uses the so-called parallel postulate
(numbered 5). Objection to the use of parallel postulate and alternative view of proposition 29 have been a major problem in foundation of what is now called non-Euclidean geometry.
The treatise of Khayyám can be considered as the first treatment of parallels axiom which is not based on petitio principii but on more intuitive postulate. Khayyám refutes the previous attempts by other Greek and Persian mathematicians to prove the proposition. And he, as Aristotle, refuses the use of motion in geometry and therefore dismisses the different attempt by Ibn Haytham too. In a sense he made the first attempt at formulating a non-Euclidean postulate as an alternative to the parallel postulate,
s but rather line segment
s. In this regard Khayyám's work can be considered the first systematic study and the first exact method of solving cubic equations.
In an untitled writing on cubic equations by Khayyám discovered in 20th century, where the above quote appears, Khayyám works on problems of geometric algebra. First is the problem of "finding a point on a quadrant
of a circle such that when a normal
is dropped from the point to one of the bounding radii, the ratio of the normal's length to that of the radius equals the ratio of the segments determined by the foot of the normal." Again in solving this problem, he reduces it to another geometric problem: "find a right triangle
having the property that the hypotenuse
equals the sum of one leg (i.e. side) plus the altitude
on the hypotenuse. To solve this geometric problem, he specializes a parameter and reaches the cubic equation . Indeed, he finds a positive root for this equation by intersecting a hyperbola
. Indeed, he finds a positive root for this equation by intersecting a hyperbola
with a circle.
This particular geometric solution of cubic equations has been further investigated and extended to degree four equations.
Regarding more general equations he states that the solution of cubic equations requires the use of conic sections and that it cannot be solved by ruler and compass methods. A proof of this impossibility was plausible only 750 years after Khayyám died. In this paper Khayyám mentions his will to prepare a paper giving full solution to cubic equations: "If the opportunity arises and I can succeed, I shall give all these fourteen forms with all their branches and cases, and how to distinguish whatever is possible or impossible so that a paper, containing elements which are greatly useful in this art will be prepared."
This refers to the book Treatise on Demonstrations of Problems of Algebra (1070), which laid down the principles of algebra, part of the body of Persian Mathematics that was eventually transmitted to Europe. In particular, he derived general methods for solving cubic equations and even some higher orders.
was first considered by Khayyám in the late 11th century in Book I of Explanations of the Difficulties in the Postulates of Euclid. Unlike many commentators on Euclid before and after him (including of course Saccheri), Khayyám was not trying to prove the parallel postulate
as such but to derive it from an equivalent postulate he formulated from "the principles of the Philosopher" (Aristotle
):
Khayyám then considered the three cases (right, obtuse, and acute) that the summit angles of a Saccheri quadrilateral can take and after proving a number of theorems about them, he (correctly) refuted the obtuse and acute cases based on his postulate and hence derived the classic postulate of Euclid.
It wasn't until 600 years later that Giordano Vitale made an advance on Khayyám in his book Euclide restituo (1680, 1686), when he used the quadrilateral to prove that if three points are equidistant on the base AB and the summit CD, then AB and CD are everywhere equidistant. Saccheri himself based the whole of his long, heroic, and ultimately flawed proof of the parallel postulate around the quadrilateral and its three cases, proving many theorems about its properties along the way.
 Like most Persian mathematicians of the period, Khayyám was famous as an astronomer
Like most Persian mathematicians of the period, Khayyám was famous as an astronomer
.
In 1073, the Seljuk
Sultan
Sultan Jalal al-Din Malekshah Saljuqi
(Malik-Shah I, 1072–92), invited Khayyám to build an observatory
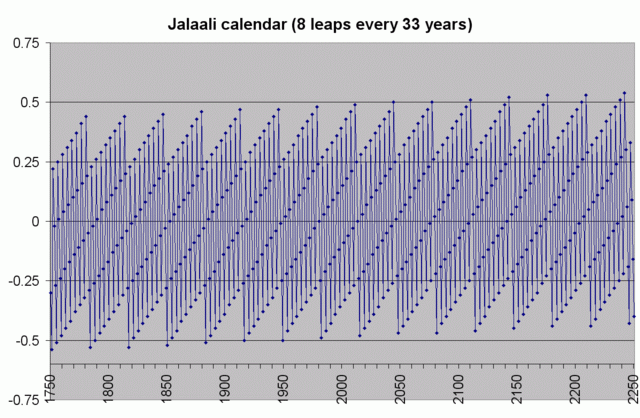
, along with various other distinguished scientists. According to some accounts, the version of the medieval Iranian calendar in which 2,820 solar years together contain 1,029,983 days (or 683 leap years, for an average year length of 365.24219858156 days) was based on the measurements of Khayyám and his colleagues. Another proposal is that Khayyám's calendar simply contained eight leap years every thirty-three years (for a year length of 365.2424 days). In either case, his calendar was more accurate to the mean tropical year than the Gregorian calendar of 500 years later. The modern Iranian calendar is based on his calculations.
This calendar was known as Jalali calendar after the Sultan, and was in force across Greater Iran
from the 11th to the 20th centuries. It is the basis of the Iranian calendar
which is followed today in Iran and Afghanistan. While the Jalali calendar is more accurate than the Gregorian, it is based on actual solar transit, (similar to Hindu calendar
s), and requires an Ephemeris
for calculating dates. The lengths of the months can vary between 29 and 31 days depending on the moment when the sun crossed into a new zodiac
al area (an attribute common to most Hindu calendar
s). This meant that seasonal errors were lower than in the Gregorian calendar.
The modern-day Iranian calendar standardizes the month lengths based on a reform from 1925, thus minimizing the effect of solar transits. Seasonal errors are somewhat higher than in the Jalali version, but leap years are calculated as before.
 He is believed to have written about a thousand four-line verses or rubaiyat (quatrains). In the English-speaking world, he was introduced through the Rubáiyát of Omar Khayyám
He is believed to have written about a thousand four-line verses or rubaiyat (quatrains). In the English-speaking world, he was introduced through the Rubáiyát of Omar Khayyám
which are rather free-wheeling English translations by Edward FitzGerald
(1809–1883). Other English translations of parts of the rubáiyát (rubáiyát meaning "quatrains") exist, but FitzGerald's are the most well known.
Ironically, FitzGerald's translations reintroduced Khayyám to Iranians "who had long ignored the Neishapouri poet." A 1934 book by one of Iran's most prominent writers, Sadeq Hedayat, Songs of Khayyam, (Taranehha-ye Khayyam) is said to have "shaped the way a generation of Iranians viewed" the poet.
Khayyam's poetry is translated to many languages.
Khayyám's personal beliefs are not known with certainty, but much is discernible from his poetic oeuvre.
literal, poetic and less controversial than that of Edward Fitzgerald
.
The Moving Finger
writes; and, having writ,
Moves on: nor all thy Piety nor Wit,
Shall lure it back to cancel half a Line
,
Nor all thy Tear
s wash out a Word of it.
But helpless pieces in the game He plays,
Upon this chequer-board of Night
s and Day
s,
He hither and thither moves, and checks ... and slays,
Then one by one, back in the Closet
lays.
And, as the Cock crew, those who stood before
The Tavern shouted - "Open then the Door!
You know how little time we have to stay,
And once departed, may return no more."
A Book
of Verses underneath the Bough,
A Jug of Wine, a Loaf of Bread
--and Thou,
Beside me singing in the Wilderness,
And oh, Wilderness is Paradise enow.
If chance supplied a loaf of white bread,
Two casks of wine and a leg of mutton,
In the corner of a garden with a tulip-cheeked girl,
There'd be enjoyment no Sultan
could outdo.
Myself when young did eagerly frequent
Doctor
and Saint, and heard great Argument
About it and about: but evermore
Came out of the same Door as in I went.
With them the Seed
of Wisdom did I sow,
And with my own hand labour'd it to grow:
And this was all the Harvest
that I reap'd -
"I came like Water, and like Wind I go."
Into this Universe
, and why not knowing,
Nor whence, like Water willy-nilly flowing:
And out of it, as Wind along the Waste,
I know not whither, willy-nilly blowing.
And that inverted Bowl
we call The Sky
,
Whereunder crawling coop't we live and die,
Lift not thy hands to It for help - for It
Rolls impotently on as Thou or I.
.........................................
no other Iranian writer/scholar is viewed in such extremely differing ways. At one end of the spectrum there are nightclubs named after Khayyám, and he is seen as an agnostic hedonist. On the other end of the spectrum, he is seen as a mystical Sufi poet influenced by platonic traditions.
The verse: "Enjoy wine and women and don't be afraid, Allah has compassion," suggests that he was not an atheist. He further believes that it is almost certain that Khayyám objected to the notion that every particular event and phenomenon was the result of divine intervention. Nor did he zealously believe in an afterlife with a Judgment Day or rewards and punishments. Instead, he supported the view that laws of nature explained all phenomena of observed life. One contemporary writes: "I did not observe that he had any great belief in astrological predictions or speculations; nor have I seen or heard of any of the great (scientists) who had such belief."
The following two quatrains are representative of numerous others that serve to reject many tenets of religious dogma:
which translates in FitzGerald's work as:
A more literal translation could read:
which FitzGerald has erroneously and mistakenly interpreted as:
A literal translation, in an ironic echo of "all is vanity", could read:
But some specialists, like Seyyed Hossein Nasr
who looks at the available philosophical works of Khayyám, maintain that it is really reductive to just look at the poems (which are sometimes doubtful) to establish his personal views about God or religion; in fact, he even wrote a treatise entitled "al-Khutbat al-gharrå˘" (The Splendid Sermon) on the praise of God, where he holds orthodox views, agreeing with Avicenna
on Divine Unity
. In fact, this treatise is not an exception, and S.H. Nasr
gives an example where he identified himself as a Sufi, after criticizing different methods of knowing God, preferring the intuition over the rational (opting for the so-called "kashf
", or unveiling, method):
The same author goes on by giving other philosophical writings which are totally compatible with the religion of Islam, as the "al-Risålah fil-wujud" (Treatise on Being), written in Arabic, which begin with Quranic verses and asserting that all things come from God, and there is an order in these things. In another work, "Risålah jawåban li-thalåth maså˘il" (Treatise of Response
to Three Questions), he gives a response to question on, for instance, the becoming of the soul post-mortem. S.H. Nasr
even gives some poetry where he is perfectly in favor of Islamic orthodoxy, but expressing mystical views (God's goodness, the ephemerical state of this life, ...):
Considering misunderstandings about Khayyám in the West and elsewhere, S.H. Nasr
concludes by saying that if a correct study of the authentic rubaiyat is done, but along with the philosophical works, or even the spiritual biography entitled Sayr wa sulak (Spiritual Wayfaring), we can no longer view the man as a simple hedonistic wine-lover, or even an early skeptic, but a profound mystical thinker and scientist whose works are more important than some verses. C.H.A. Bjerregaard earlier summarised the situation:
Abdullah Dougan
, a modern Naqshbandi
Sufi
, provides commentary on the role and contribution of Omar Khayyam to Sufi
thought. Dougan says that while Omar is a minor Sufi teacher compared to the giants – Rumi, Attar and Sana’i
– one aspect that makes Omar’s work so relevant and accessible is its very human scale as we can feel for him and understand his approach. The argument over the quality of Fitzgerald’s translation of the Rubaiyat has, according to Dougan, diverted attention from a fuller understanding of the deeply esoteric message contained in Omar’s actual material – "Every line of the Rubaiyat has more meaning than almost anything you could read in Sufi literature".
 Khayyám himself rejects to be associated with the title falsafi- (lit. philosopher) in the sense of Aristotelian one and stressed he wishes "to know who I am". In the context of philosophers he was labeled by some of his contemporaries as "detached from divine blessings".
Khayyám himself rejects to be associated with the title falsafi- (lit. philosopher) in the sense of Aristotelian one and stressed he wishes "to know who I am". In the context of philosophers he was labeled by some of his contemporaries as "detached from divine blessings".
It is now established that Khayyám taught for decades the philosophy of Avicena, especially "the Book of Healing
", in his home town Nishapur
, till his death. In an incident he had been requested to comment on a disagreement between Avicena and a philosopher called Abu'l-Barakat (known also as Nathanel) who had criticized Avicena strongly. Khayyám is said to have answered "[he] does not even understand the sense of the words of Avicenna, how can he oppose what he does not know?"
Khayyám the philosopher could be understood from two rather distinct sources. One is through his Rubaiyat
and the other through his own works in light of the intellectual and social conditions of his time. The latter could be informed by the evaluations of Khayyám's works by scholars and philosophers such as Bayhaqi, Nezami Aruzi, and Zamakhshari and Sufi poets and writers Attar Nishapuri and Najmeddin Razi
.
As a mathematician, Khayyám has made fundamental contributions to the Philosophy of mathematics
especially in the context of Persian Mathematics and Persian philosophy with which most of the other Persian scientists and philosophers such as Avicenna
, Biruni, and Tusi
are associated. There are at least three basic mathematical ideas of strong philosophical dimensions that can be associated with Khayyám.
was a
Persian polymath
Polymath
A polymath is a person whose expertise spans a significant number of different subject areas. In less formal terms, a polymath may simply be someone who is very knowledgeable...
: philosopher, mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, astronomer
Astronomer
An astronomer is a scientist who studies celestial bodies such as planets, stars and galaxies.Historically, astronomy was more concerned with the classification and description of phenomena in the sky, while astrophysics attempted to explain these phenomena and the differences between them using...
and poet
Persian literature
Persian literature spans two-and-a-half millennia, though much of the pre-Islamic material has been lost. Its sources have been within historical Persia including present-day Iran as well as regions of Central Asia where the Persian language has historically been the national language...
. He also wrote treatises on mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
, geography
Islamic geography
Geography and cartography in medieval Islam refers to the advancement of geography, cartography and the earth sciences in the medieval Islamic civilization....
, mineralogy
Mineralogy
Mineralogy is the study of chemistry, crystal structure, and physical properties of minerals. Specific studies within mineralogy include the processes of mineral origin and formation, classification of minerals, their geographical distribution, as well as their utilization.-History:Early writing...
, music
Music
Music is an art form whose medium is sound and silence. Its common elements are pitch , rhythm , dynamics, and the sonic qualities of timbre and texture...
, climatology
Climatology
Climatology is the study of climate, scientifically defined as weather conditions averaged over a period of time, and is a branch of the atmospheric sciences...
and theology
Islamic theology
Islamic theology is a branch of Islamic studies regarding the beliefs associated with the Islamic faith. Any religious belief system, or creed, can be considered an example of aqidah. However, this term has taken a significant technical usage in Islamic history and theology, denoting those...
.
Born in Nishapur
Nishapur
Nishapur or Nishabur , is a city in the Razavi Khorasan province in northeastern Iran, situated in a fertile plain at the foot of the Binalud Mountains, near the regional capital of Mashhad...
, at a young age he moved to Samarkand
Samarkand
Although a Persian-speaking region, it was not united politically with Iran most of the times between the disintegration of the Seleucid Empire and the Arab conquest . In the 6th century it was within the domain of the Turkic kingdom of the Göktürks.At the start of the 8th century Samarkand came...
and obtained his education there, afterwards he moved to Bukhara
Bukhara
Bukhara , from the Soghdian βuxārak , is the capital of the Bukhara Province of Uzbekistan. The nation's fifth-largest city, it has a population of 263,400 . The region around Bukhara has been inhabited for at least five millennia, and the city has existed for half that time...
and became established as one of the major mathematicians and astronomers of the medieval period. He is the author of one of the most important treatises on algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
written before modern times, the Treatise on Demonstration of Problems of Algebra, which includes a geometric method for solving cubic equations by intersecting a hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
with a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
. He contributed to a calendar reform
Calendar reform
A calendar reform is any significant revision of a calendar system. The term sometimes is used instead for a proposal to switch to a different calendar.Most calendars have several rules which could be altered by reform:...
.
His significance as a philosopher and teacher, and his few remaining philosophical works, have not received the same attention as his scientific and poetic writings. Zamakhshari referred to him as “the philosopher of the world”. Many sources have testified that he taught for decades the philosophy of Ibn Sina in Nishapur
Nishapur
Nishapur or Nishabur , is a city in the Razavi Khorasan province in northeastern Iran, situated in a fertile plain at the foot of the Binalud Mountains, near the regional capital of Mashhad...
where Khayyám was born and buried and where his mausoleum today remains a masterpiece of Iranian architecture
Iranian architecture
Iranian architecture or Persian architecture is the architecture of Iran . It has a continuous history from at least 5000 BCE to the present, with characteristic examples distributed over a vast area from Turkey to North India and the borders of China and from the Caucasus to Zanzibar...
visited by many people every year.
Outside Iran and Persian speaking countries, Khayyám has had an impact on literature and societies through the translation of his works and popularization by other scholars. The greatest such impact was in English-speaking countries; the English scholar Thomas Hyde
Thomas Hyde
Thomas Hyde was an English orientalist. The first use of the word dualism is attributed to him, in 1700.-Life:He was born at Billingsley, near Bridgnorth in Shropshire, on 29 June 1636...
(1636–1703) was the first non-Persian to study him. The most influential of all was Edward FitzGerald
Edward FitzGerald (poet)
Edward FitzGerald was an English writer, best known as the poet of the first and most famous English translation of The Rubaiyat of Omar Khayyam. The spelling of his name as both FitzGerald and Fitzgerald is seen...
(1809–83), who made Khayyám the most famous poet of the East in the West through his celebrated translation and adaptations of Khayyám's rather small number of quatrain
Quatrain
A quatrain is a stanza, or a complete poem, consisting of four lines of verse. Existing in various forms, the quatrain appears in poems from the poetic traditions of various ancient civilizations including Ancient Greece, Ancient Rome, and China; and, continues into the 21st century, where it is...
s (rubaiyaas) in Rubáiyát of Omar Khayyám
Rubaiyat of Omar Khayyam
The Rubáiyát of Omar Khayyám is the title that Edward FitzGerald gave to his translation of a selection of poems, originally written in Persian and of which there are about a thousand, attributed to Omar Khayyám , a Persian poet, mathematician and astronomer...
.
Early life
Khayyám's full name was Ghiyath al-Din Abu'l-Fath 'Umar ibn Ibrahim Al-Nishapuri al-Khayyami . He was born in NishapurNishapur
Nishapur or Nishabur , is a city in the Razavi Khorasan province in northeastern Iran, situated in a fertile plain at the foot of the Binalud Mountains, near the regional capital of Mashhad...
,(modern-day Iran
Iran
Iran , officially the Islamic Republic of Iran , is a country in Southern and Western Asia. The name "Iran" has been in use natively since the Sassanian era and came into use internationally in 1935, before which the country was known to the Western world as Persia...
), then a Seljuq
Great Seljuq Empire
The Great Seljuq Empire was a medieval Persianate, Turko-Persian Sunni Muslim empire, originating from the Qynyq branch of Oghuz Turks. The Seljuq Empire controlled a vast area stretching from the Hindu Kush to eastern Anatolia and from Central Asia to the Persian Gulf...
capital in Khorasan
Greater Khorasan
Greater Khorasan or Ancient Khorasan is a historical region of Greater Iran mentioned in sources from Sassanid and Islamic eras which "frequently" had a denotation wider than current three provinces of Khorasan in Iran...
, which rivaled Cairo
Cairo
Cairo , is the capital of Egypt and the largest city in the Arab world and Africa, and the 16th largest metropolitan area in the world. Nicknamed "The City of a Thousand Minarets" for its preponderance of Islamic architecture, Cairo has long been a centre of the region's political and cultural life...
or Baghdad
Baghdad
Baghdad is the capital of Iraq, as well as the coterminous Baghdad Governorate. The population of Baghdad in 2011 is approximately 7,216,040...
in cultural prominence in that era. He is thought to have been born into a family of tent makers (khayyami, lit. in Farsi "tent-maker"), which he would make this into a play on words later in life:
He spent part of his childhood in the town of Balkh
Balkh
Balkh , was an ancient city and centre of Zoroastrianism in what is now northern Afghanistan. Today it is a small town in the province of Balkh, about 20 kilometers northwest of the provincial capital, Mazar-e Sharif, and some south of the Amu Darya. It was one of the major cities of Khorasan...
(present northern Afghanistan
Afghanistan
Afghanistan , officially the Islamic Republic of Afghanistan, is a landlocked country located in the centre of Asia, forming South Asia, Central Asia and the Middle East. With a population of about 29 million, it has an area of , making it the 42nd most populous and 41st largest nation in the world...
), studying under the well-known scholar Sheikh Muhammad Mansuri. He later studied under Imam
Imam
An imam is an Islamic leadership position, often the worship leader of a mosque and the Muslim community. Similar to spiritual leaders, the imam is the one who leads Islamic worship services. More often, the community turns to the mosque imam if they have a religious question...
Mowaffaq Nishapuri, who was considered one of the greatest teachers of the Khorasan
Greater Khorasan
Greater Khorasan or Ancient Khorasan is a historical region of Greater Iran mentioned in sources from Sassanid and Islamic eras which "frequently" had a denotation wider than current three provinces of Khorasan in Iran...
region. Throughout his life Omar Khayyám was dedicated to his efforts and abilities, in the day he would teach Algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
and Geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
in the evening he would attend the Seljuq court as an adviser of Malik-Shah I and at night he would study Astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
and complete the important aspects of the Jalali calendar.
Omar Khayyám's years in Isfahan were very productive ones but after the death of the Seljuq Sultan
Sultan
Sultan is a title with several historical meanings. Originally, it was an Arabic language abstract noun meaning "strength", "authority", "rulership", and "dictatorship", derived from the masdar سلطة , meaning "authority" or "power". Later, it came to be used as the title of certain rulers who...
Malik-Shah I (presumably by the Assassins sect), the Sultan's widow turned against him as an adviser and and soon therefore Omar Khayyám set out on his Hajj
Hajj
The Hajj is the pilgrimage to Mecca, Saudi Arabia. It is one of the largest pilgrimages in the world, and is the fifth pillar of Islam, a religious duty that must be carried out at least once in their lifetime by every able-bodied Muslim who can afford to do so...
or Pilgrimage to Mecca
Mecca
Mecca is a city in the Hijaz and the capital of Makkah province in Saudi Arabia. The city is located inland from Jeddah in a narrow valley at a height of above sea level...
and Medina
Medina
Medina , or ; also transliterated as Madinah, or madinat al-nabi "the city of the prophet") is a city in the Hejaz region of western Saudi Arabia, and serves as the capital of the Al Madinah Province. It is the second holiest city in Islam, and the burial place of the Islamic Prophet Muhammad, and...
. He was then allowed to work as a court astrologer and was permitted to return to Nishapur
Nishapur
Nishapur or Nishabur , is a city in the Razavi Khorasan province in northeastern Iran, situated in a fertile plain at the foot of the Binalud Mountains, near the regional capital of Mashhad...
where he was famous for works and continued to teach mathematics, astronomy and even medicine.
Mathematician
Khayyám was famous during his times as a mathematicianMathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
. He wrote the influential Treatise on Demonstration of Problems of Algebra (1070), which laid down the principles of algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, part of the body of Persian Mathematics that was eventually transmitted to Europe. In particular, he derived general methods for solving cubic equations and even some higher orders.

Triangular array
In mathematics and computing, a triangular array of numbers, polynomials, or the like, is a doubly indexed sequence in which each row is only as long as the row's own index.Notable particular examples include these:...
of binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s known as Pascal's triangle
Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients in a triangle. It is named after the French mathematician, Blaise Pascal...
. In 1077, Khayyám wrote Sharh ma ashkala min musadarat kitab Uqlidis (Explanations of the Difficulties in the Postulates of Euclid) published in English as "On the Difficulties of Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
's Definitions". An important part of the book is concerned with Euclid's famous parallel postulate, which attracted the interest of Thabit ibn Qurra
Thabit ibn Qurra
' was a mathematician, physician, astronomer and translator of the Islamic Golden Age.Ibn Qurra made important discoveries in algebra, geometry and astronomy...
. Al-Haytham had previously attempted a demonstration of the postulate; Khayyám's attempt was a distinct advance, and his criticisms made their way to Europe, and may have contributed to the eventual development of non-Euclidean geometry
Non-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
.
Omar Khayyám had notable works in geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, specifically on the theory of proportions, his notable contemporary mathematicians included Al-Khazini
Al-Khazini
Abu al-Fath Abd al-Rahman Mansour al-Khāzini or simply Abu al-Fath Khāzini was a Muslim astronomer of Greek ethnicity from Merv, then in the Khorasan province of Persia .-References:...
and Abu Hatim al-Muzaffar ibn Ismail al-Isfizari
Theory of parallels

The first section is a treatise containing some propositions and lemmas concerning the parallel postulate. It has reached the Western world from a reproduction in a manuscript written in 1387-88 AD by the Persian mathematician Tusi. Tusi mentions explicitly that he re-writes the treatise "in Khayyám's own words" and quotes Khayyám, saying that "they are worth adding to Euclid's Elements (first book) after Proposition 28." This proposition states a condition enough for having two lines in plane parallel to one another. After this proposition follows another, numbered 29, which is converse to the previous one. The proof of Euclid uses the so-called parallel postulate
Parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
(numbered 5). Objection to the use of parallel postulate and alternative view of proposition 29 have been a major problem in foundation of what is now called non-Euclidean geometry.
The treatise of Khayyám can be considered as the first treatment of parallels axiom which is not based on petitio principii but on more intuitive postulate. Khayyám refutes the previous attempts by other Greek and Persian mathematicians to prove the proposition. And he, as Aristotle, refuses the use of motion in geometry and therefore dismisses the different attempt by Ibn Haytham too. In a sense he made the first attempt at formulating a non-Euclidean postulate as an alternative to the parallel postulate,
Geometric algebra
This philosophical view of mathematics (see below) has had a significant impact on Khayyám's celebrated approach and method in geometric algebra and in particular in solving cubic equations. In that his solution is not a direct path to a numerical solution and in fact his solutions are not numberNumber
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
s but rather line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
s. In this regard Khayyám's work can be considered the first systematic study and the first exact method of solving cubic equations.
In an untitled writing on cubic equations by Khayyám discovered in 20th century, where the above quote appears, Khayyám works on problems of geometric algebra. First is the problem of "finding a point on a quadrant
Circular sector
A circular sector or circle sector, is the portion of a disk enclosed by two radii and an arc, where the smaller area is known as the minor sector and the larger being the major sector. In the diagram, θ is the central angle in radians, r the radius of the circle, and L is the arc length of the...
of a circle such that when a normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
is dropped from the point to one of the bounding radii, the ratio of the normal's length to that of the radius equals the ratio of the segments determined by the foot of the normal." Again in solving this problem, he reduces it to another geometric problem: "find a right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
having the property that the hypotenuse
Hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
equals the sum of one leg (i.e. side) plus the altitude
Altitude (triangle)
In geometry, an altitude of a triangle is a straight line through a vertex and perpendicular to a line containing the base . This line containing the opposite side is called the extended base of the altitude. The intersection between the extended base and the altitude is called the foot of the...
on the hypotenuse. To solve this geometric problem, he specializes a parameter and reaches the cubic equation
 . Indeed, he finds a positive root for this equation by intersecting a hyperbola
. Indeed, he finds a positive root for this equation by intersecting a hyperbolaHyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
with a circle.
This particular geometric solution of cubic equations has been further investigated and extended to degree four equations.
Regarding more general equations he states that the solution of cubic equations requires the use of conic sections and that it cannot be solved by ruler and compass methods. A proof of this impossibility was plausible only 750 years after Khayyám died. In this paper Khayyám mentions his will to prepare a paper giving full solution to cubic equations: "If the opportunity arises and I can succeed, I shall give all these fourteen forms with all their branches and cases, and how to distinguish whatever is possible or impossible so that a paper, containing elements which are greatly useful in this art will be prepared."
This refers to the book Treatise on Demonstrations of Problems of Algebra (1070), which laid down the principles of algebra, part of the body of Persian Mathematics that was eventually transmitted to Europe. In particular, he derived general methods for solving cubic equations and even some higher orders.
Binomial theorem and extraction of roots
This particular remark of Khayyám and certain propositions found in his Algebra book has made some historians of mathematics believe that Khayyám had indeed a binomial theorem up to any power. The case of power 2 is explicitly stated in Euclid's elements and the case of at most power 3 had been established by Indian mathematicians. Khayyám was the mathematician who noticed the importance of a general binomial theorem. The argument supporting the claim that Khayyám had a general binomial theorem is based on his ability to extract roots.Khayyám-Saccheri quadrilateral
The Saccheri quadrilateralSaccheri quadrilateral
A Saccheri quadrilateral is a quadrilateral with two equal sides perpendicular to the base. It is named after Giovanni Gerolamo Saccheri, who used it extensively in his book Euclid vindicatus , an attempt to prove the parallel postulate using the method Reductio ad absurdum...
was first considered by Khayyám in the late 11th century in Book I of Explanations of the Difficulties in the Postulates of Euclid. Unlike many commentators on Euclid before and after him (including of course Saccheri), Khayyám was not trying to prove the parallel postulate
Parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
as such but to derive it from an equivalent postulate he formulated from "the principles of the Philosopher" (Aristotle
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
):
- Two convergent straight lines intersect and it is impossible for two convergent straight lines to diverge in the direction in which they converge.
Khayyám then considered the three cases (right, obtuse, and acute) that the summit angles of a Saccheri quadrilateral can take and after proving a number of theorems about them, he (correctly) refuted the obtuse and acute cases based on his postulate and hence derived the classic postulate of Euclid.
It wasn't until 600 years later that Giordano Vitale made an advance on Khayyám in his book Euclide restituo (1680, 1686), when he used the quadrilateral to prove that if three points are equidistant on the base AB and the summit CD, then AB and CD are everywhere equidistant. Saccheri himself based the whole of his long, heroic, and ultimately flawed proof of the parallel postulate around the quadrilateral and its three cases, proving many theorems about its properties along the way.
Astronomer

Astronomer
An astronomer is a scientist who studies celestial bodies such as planets, stars and galaxies.Historically, astronomy was more concerned with the classification and description of phenomena in the sky, while astrophysics attempted to explain these phenomena and the differences between them using...
.
In 1073, the Seljuk
Great Seljuq Empire
The Great Seljuq Empire was a medieval Persianate, Turko-Persian Sunni Muslim empire, originating from the Qynyq branch of Oghuz Turks. The Seljuq Empire controlled a vast area stretching from the Hindu Kush to eastern Anatolia and from Central Asia to the Persian Gulf...
Sultan
Sultan
Sultan is a title with several historical meanings. Originally, it was an Arabic language abstract noun meaning "strength", "authority", "rulership", and "dictatorship", derived from the masdar سلطة , meaning "authority" or "power". Later, it came to be used as the title of certain rulers who...
Sultan Jalal al-Din Malekshah Saljuqi
Malik Shah I
Jalāl al-Dawlah Malik-shāh was born in 1055, succeeded Alp Arslan as the Seljuq Sultan in 1072, and reigned until his death in 1092....
(Malik-Shah I, 1072–92), invited Khayyám to build an observatory
Observatory
An observatory is a location used for observing terrestrial or celestial events. Astronomy, climatology/meteorology, geology, oceanography and volcanology are examples of disciplines for which observatories have been constructed...
, along with various other distinguished scientists. According to some accounts, the version of the medieval Iranian calendar in which 2,820 solar years together contain 1,029,983 days (or 683 leap years, for an average year length of 365.24219858156 days) was based on the measurements of Khayyám and his colleagues. Another proposal is that Khayyám's calendar simply contained eight leap years every thirty-three years (for a year length of 365.2424 days). In either case, his calendar was more accurate to the mean tropical year than the Gregorian calendar of 500 years later. The modern Iranian calendar is based on his calculations.
Calendar reform
Khayyám is claimed to be a member of a panel that introduced several reforms to the Persian calendar. On March 15, 1079, Sultan Malik Shah I accepted this corrected calendar as the official Persian calendar.This calendar was known as Jalali calendar after the Sultan, and was in force across Greater Iran
Greater Iran
Greater Iran refers to the regions that have significant Iranian cultural influence. It roughly corresponds to the territory on the Iranian plateau and its bordering plains, stretching from Iraq, the Caucasus, and Turkey in the west to the Indus River in the east...
from the 11th to the 20th centuries. It is the basis of the Iranian calendar
Iranian calendar
The Iranian calendars or sometimes called Persian calendars are a succession of calendars invented or used for over two millennia in Greater Iran...
which is followed today in Iran and Afghanistan. While the Jalali calendar is more accurate than the Gregorian, it is based on actual solar transit, (similar to Hindu calendar
Hindu calendar
The hindu calendar used in ancient times has undergone many changes in the process of regionalization, and today there are several regional Indian calendars, as well as an Indian national calendar. Nepali calendar, Bengali calendar, Malayalam calendar, Tamil calendar, Telugu calendar, Kannada...
s), and requires an Ephemeris
Ephemeris
An ephemeris is a table of values that gives the positions of astronomical objects in the sky at a given time or times. Different kinds of ephemerides are used for astronomy and astrology...
for calculating dates. The lengths of the months can vary between 29 and 31 days depending on the moment when the sun crossed into a new zodiac
Zodiac
In astronomy, the zodiac is a circle of twelve 30° divisions of celestial longitude which are centred upon the ecliptic: the apparent path of the Sun across the celestial sphere over the course of the year...
al area (an attribute common to most Hindu calendar
Hindu calendar
The hindu calendar used in ancient times has undergone many changes in the process of regionalization, and today there are several regional Indian calendars, as well as an Indian national calendar. Nepali calendar, Bengali calendar, Malayalam calendar, Tamil calendar, Telugu calendar, Kannada...
s). This meant that seasonal errors were lower than in the Gregorian calendar.
The modern-day Iranian calendar standardizes the month lengths based on a reform from 1925, thus minimizing the effect of solar transits. Seasonal errors are somewhat higher than in the Jalali version, but leap years are calculated as before.
Poet

Rubaiyat of Omar Khayyam
The Rubáiyát of Omar Khayyám is the title that Edward FitzGerald gave to his translation of a selection of poems, originally written in Persian and of which there are about a thousand, attributed to Omar Khayyám , a Persian poet, mathematician and astronomer...
which are rather free-wheeling English translations by Edward FitzGerald
Edward FitzGerald (poet)
Edward FitzGerald was an English writer, best known as the poet of the first and most famous English translation of The Rubaiyat of Omar Khayyam. The spelling of his name as both FitzGerald and Fitzgerald is seen...
(1809–1883). Other English translations of parts of the rubáiyát (rubáiyát meaning "quatrains") exist, but FitzGerald's are the most well known.
Ironically, FitzGerald's translations reintroduced Khayyám to Iranians "who had long ignored the Neishapouri poet." A 1934 book by one of Iran's most prominent writers, Sadeq Hedayat, Songs of Khayyam, (Taranehha-ye Khayyam) is said to have "shaped the way a generation of Iranians viewed" the poet.
Khayyam's poetry is translated to many languages.
Khayyám's personal beliefs are not known with certainty, but much is discernible from his poetic oeuvre.
Poetry
Omar Khayyám's poems have been translated many times in many languages and many translators have claimed that their translations of the Rubáiyát of Omar KhayyámRubaiyat of Omar Khayyam
The Rubáiyát of Omar Khayyám is the title that Edward FitzGerald gave to his translation of a selection of poems, originally written in Persian and of which there are about a thousand, attributed to Omar Khayyám , a Persian poet, mathematician and astronomer...
literal, poetic and less controversial than that of Edward Fitzgerald
Edward Fitzgerald
Edward Fitzgerald may refer to:* Lord Edward FitzGerald , Irish revolutionary*Edward Fitzgerald , Irish* Edward FitzGerald, 7th Duke of Leinster * Edward Fitzgerald...
.
The Moving Finger
Finger
A finger is a limb of the human body and a type of digit, an organ of manipulation and sensation found in the hands of humans and other primates....
writes; and, having writ,
Moves on: nor all thy Piety nor Wit,
Shall lure it back to cancel half a Line
Line
- Science and technology :* Line , a circuit or loop.** A power line for electric power transmission** line power or lines power, domestic mains electricity.** telephone line** RF transmission line...
,
Nor all thy Tear
Tear
Tear may refer to:*Tears, a type of eye secretion*Tearing, the ripping apart of something by force*Robert Tear, a Welsh singer-Elements in fiction:*Tear, a character Tear Grants in video game Tales of the Abyss...
s wash out a Word of it.
But helpless pieces in the game He plays,
Upon this chequer-board of Night
Night
Night or nighttime is the period of time when the sun is below the horizon. This occurs after dusk. The opposite of night is day...
s and Day
Day
A day is a unit of time, commonly defined as an interval equal to 24 hours. It also can mean that portion of the full day during which a location is illuminated by the light of the sun...
s,
He hither and thither moves, and checks ... and slays,
Then one by one, back in the Closet
Closet
A closet is a small and enclosed space, a cabinet, or a cupboard in a house or building used for general storage or hanging clothes. A closet for food storage is usually referred to as a pantry...
lays.
And, as the Cock crew, those who stood before
The Tavern shouted - "Open then the Door!
You know how little time we have to stay,
And once departed, may return no more."
A Book
Book
A book is a set or collection of written, printed, illustrated, or blank sheets, made of hot lava, paper, parchment, or other materials, usually fastened together to hinge at one side. A single sheet within a book is called a leaf or leaflet, and each side of a leaf is called a page...
of Verses underneath the Bough,
A Jug of Wine, a Loaf of Bread
Bread
Bread is a staple food prepared by cooking a dough of flour and water and often additional ingredients. Doughs are usually baked, but in some cuisines breads are steamed , fried , or baked on an unoiled frying pan . It may be leavened or unleavened...
--and Thou,
Beside me singing in the Wilderness,
And oh, Wilderness is Paradise enow.
If chance supplied a loaf of white bread,
Two casks of wine and a leg of mutton,
In the corner of a garden with a tulip-cheeked girl,
There'd be enjoyment no Sultan
Sultan
Sultan is a title with several historical meanings. Originally, it was an Arabic language abstract noun meaning "strength", "authority", "rulership", and "dictatorship", derived from the masdar سلطة , meaning "authority" or "power". Later, it came to be used as the title of certain rulers who...
could outdo.
Myself when young did eagerly frequent
Doctor
Physician
A physician is a health care provider who practices the profession of medicine, which is concerned with promoting, maintaining or restoring human health through the study, diagnosis, and treatment of disease, injury and other physical and mental impairments...
and Saint, and heard great Argument
About it and about: but evermore
Came out of the same Door as in I went.
With them the Seed
Seed
A seed is a small embryonic plant enclosed in a covering called the seed coat, usually with some stored food. It is the product of the ripened ovule of gymnosperm and angiosperm plants which occurs after fertilization and some growth within the mother plant...
of Wisdom did I sow,
And with my own hand labour'd it to grow:
And this was all the Harvest
Harvest
Harvest is the process of gathering mature crops from the fields. Reaping is the cutting of grain or pulse for harvest, typically using a scythe, sickle, or reaper...
that I reap'd -
"I came like Water, and like Wind I go."
Into this Universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
, and why not knowing,
Nor whence, like Water willy-nilly flowing:
And out of it, as Wind along the Waste,
I know not whither, willy-nilly blowing.
And that inverted Bowl
Bowl
Bowl or The Bowl may refer to:* Bowl , a common vessel used to serve food* Bowl , in cannabis culture, a smoking device, its bowl-shaped part, or its capacity** Bowl, a part of a smoking pipe...
we call The Sky
Sky
The sky is the part of the atmosphere or outer space visible from the surface of any astronomical object. It is difficult to define precisely for several reasons. During daylight, the sky of Earth has the appearance of a pale blue surface because the air scatters the sunlight. The sky is sometimes...
,
Whereunder crawling coop't we live and die,
Lift not thy hands to It for help - for It
Rolls impotently on as Thou or I.
.........................................
Views on religion
There have been widely divergent views on Khayyám. According to Seyyed Hossein NasrSeyyed Hossein Nasr
Seyyed Hossein Nasr is an Iranian University Professor of Islamic studies at George Washington University, and a prominent Islamic philosopher...
no other Iranian writer/scholar is viewed in such extremely differing ways. At one end of the spectrum there are nightclubs named after Khayyám, and he is seen as an agnostic hedonist. On the other end of the spectrum, he is seen as a mystical Sufi poet influenced by platonic traditions.
The verse: "Enjoy wine and women and don't be afraid, Allah has compassion," suggests that he was not an atheist. He further believes that it is almost certain that Khayyám objected to the notion that every particular event and phenomenon was the result of divine intervention. Nor did he zealously believe in an afterlife with a Judgment Day or rewards and punishments. Instead, he supported the view that laws of nature explained all phenomena of observed life. One contemporary writes: "I did not observe that he had any great belief in astrological predictions or speculations; nor have I seen or heard of any of the great (scientists) who had such belief."
The following two quatrains are representative of numerous others that serve to reject many tenets of religious dogma:
which translates in FitzGerald's work as:
- And if the Wine you drink, the Lip you press,
- End in the Nothing all Things end in — Yes —
- Then fancy while Thou art, Thou art but what
- Thou shalt be — Nothing — Thou shalt not be less.
A more literal translation could read:
- If with wine you are drunk be happy,
- If seated with a moon-faced (beautiful), be happy,
- Since the end purpose of the universe is nothing-ness;
- Hence picture your nothing-ness, then while you are, be happy!
which FitzGerald has erroneously and mistakenly interpreted as:
- Why, all the Saints and Sages who discuss’d
- Of the Two Worlds so learnedly — are thrust
- Like foolish Prophets forth; their Words to Scorn
- Are scatter’d, and their Mouths are stopt with Dust.
A literal translation, in an ironic echo of "all is vanity", could read:
- Those who have gone forth, thou cup-bearer,
- Have fallen upon the dust of pride, thou cup-bearer,
- Drink wine and hear from me the truth: air is all that they have said, thou cup-bearer.
But some specialists, like Seyyed Hossein Nasr
Seyyed Hossein Nasr
Seyyed Hossein Nasr is an Iranian University Professor of Islamic studies at George Washington University, and a prominent Islamic philosopher...
who looks at the available philosophical works of Khayyám, maintain that it is really reductive to just look at the poems (which are sometimes doubtful) to establish his personal views about God or religion; in fact, he even wrote a treatise entitled "al-Khutbat al-gharrå˘" (The Splendid Sermon) on the praise of God, where he holds orthodox views, agreeing with Avicenna
Avicenna
Abū ʿAlī al-Ḥusayn ibn ʿAbd Allāh ibn Sīnā , commonly known as Ibn Sīnā or by his Latinized name Avicenna, was a Persian polymath, who wrote almost 450 treatises on a wide range of subjects, of which around 240 have survived...
on Divine Unity
Tawhid
Tawhid is the concept of monotheism in Islam. It is the religion's most fundamental concept and holds God is one and unique ....
. In fact, this treatise is not an exception, and S.H. Nasr
Seyyed Hossein Nasr
Seyyed Hossein Nasr is an Iranian University Professor of Islamic studies at George Washington University, and a prominent Islamic philosopher...
gives an example where he identified himself as a Sufi, after criticizing different methods of knowing God, preferring the intuition over the rational (opting for the so-called "kashf
Kashf
Kashf in order to allow divine truths to pour into it. Kashf is etymologically related to mukashafa “disclosure”/ “divine irradiation of the essence”, which connotes “gain[ing] familiarity with things unseen behind the veils”...
", or unveiling, method):
The same author goes on by giving other philosophical writings which are totally compatible with the religion of Islam, as the "al-Risålah fil-wujud" (Treatise on Being), written in Arabic, which begin with Quranic verses and asserting that all things come from God, and there is an order in these things. In another work, "Risålah jawåban li-thalåth maså˘il" (Treatise of Response
to Three Questions), he gives a response to question on, for instance, the becoming of the soul post-mortem. S.H. Nasr
Seyyed Hossein Nasr
Seyyed Hossein Nasr is an Iranian University Professor of Islamic studies at George Washington University, and a prominent Islamic philosopher...
even gives some poetry where he is perfectly in favor of Islamic orthodoxy, but expressing mystical views (God's goodness, the ephemerical state of this life, ...):
- Thou hast said that Thou wilt torment me,
- But I shall fear not such a warning.
- For where Thou art, there can be no torment,
- And where Thou art not, how can such a place exist?
- The rotating wheel of heaven within which we wonder,
- Is an imaginal lamp of which we have knowledge by similitude.
- The sun is the candle and the world the lamp,
- We are like forms revolving within it.
- A drop of water falls in an ocean wide,
- A grain of dust becomes with earth allied;
- What doth thy coming, going here denote?
- A fly appeared a while, then invisible he became.
Considering misunderstandings about Khayyám in the West and elsewhere, S.H. Nasr
Seyyed Hossein Nasr
Seyyed Hossein Nasr is an Iranian University Professor of Islamic studies at George Washington University, and a prominent Islamic philosopher...
concludes by saying that if a correct study of the authentic rubaiyat is done, but along with the philosophical works, or even the spiritual biography entitled Sayr wa sulak (Spiritual Wayfaring), we can no longer view the man as a simple hedonistic wine-lover, or even an early skeptic, but a profound mystical thinker and scientist whose works are more important than some verses. C.H.A. Bjerregaard earlier summarised the situation:
Abdullah Dougan
Abdullah Isa Neil Dougan
Abdullah Isa Neil Dougan was a Sufi Sheikh of the Naqshbandi order. He ran open, Westernised groups, initially based on the Fourth Way ideas of GI Gurdjieff, with reference to Sufi, Hindu and Buddhist traditions...
, a modern Naqshbandi
Naqshbandi
Naqshbandi is one of the major Sufi spiritual orders of Sufi Islam. It is considered to be a "Potent" order.The Naqshbandi order is over 1,300 years old, and is active today...
Sufi
Sufism
Sufism or ' is defined by its adherents as the inner, mystical dimension of Islam. A practitioner of this tradition is generally known as a '...
, provides commentary on the role and contribution of Omar Khayyam to Sufi
Sufism
Sufism or ' is defined by its adherents as the inner, mystical dimension of Islam. A practitioner of this tradition is generally known as a '...
thought. Dougan says that while Omar is a minor Sufi teacher compared to the giants – Rumi, Attar and Sana’i
Sanai
Hakim Abul-Majd Majdūd ibn Ādam Sanā'ī Ghaznavi was a Afghan Sufi poet who lived in Ghazna, in what is now Afghanistan between the 11th century and the 12th century. Some people spell his name as Sanayee. He died around 1131.-Life:...
– one aspect that makes Omar’s work so relevant and accessible is its very human scale as we can feel for him and understand his approach. The argument over the quality of Fitzgerald’s translation of the Rubaiyat has, according to Dougan, diverted attention from a fuller understanding of the deeply esoteric message contained in Omar’s actual material – "Every line of the Rubaiyat has more meaning than almost anything you could read in Sufi literature".
Philosopher

It is now established that Khayyám taught for decades the philosophy of Avicena, especially "the Book of Healing
The Book of Healing
The Book of Healing is a scientific and philosophical encyclopedia written by Abū Alī ibn Sīnā from Asfahana, near Bukhara in Greater Persia. Despite its English title, it is not in fact concerned with medicine...
", in his home town Nishapur
Nishapur
Nishapur or Nishabur , is a city in the Razavi Khorasan province in northeastern Iran, situated in a fertile plain at the foot of the Binalud Mountains, near the regional capital of Mashhad...
, till his death. In an incident he had been requested to comment on a disagreement between Avicena and a philosopher called Abu'l-Barakat (known also as Nathanel) who had criticized Avicena strongly. Khayyám is said to have answered "[he] does not even understand the sense of the words of Avicenna, how can he oppose what he does not know?"
Khayyám the philosopher could be understood from two rather distinct sources. One is through his Rubaiyat
Rubaiyat of Omar Khayyam
The Rubáiyát of Omar Khayyám is the title that Edward FitzGerald gave to his translation of a selection of poems, originally written in Persian and of which there are about a thousand, attributed to Omar Khayyám , a Persian poet, mathematician and astronomer...
and the other through his own works in light of the intellectual and social conditions of his time. The latter could be informed by the evaluations of Khayyám's works by scholars and philosophers such as Bayhaqi, Nezami Aruzi, and Zamakhshari and Sufi poets and writers Attar Nishapuri and Najmeddin Razi
Najmeddin Razi
Abū Bakr 'Abdollāh b. Moḥammad b. Šahāvar b. Anūšervān al-Rāzī commonly know by the laqab, or sobriquet, of Najm al-Dīn Dāya, meaning "wetnurse"...
.
As a mathematician, Khayyám has made fundamental contributions to the Philosophy of mathematics
Philosophy of mathematics
The philosophy of mathematics is the branch of philosophy that studies the philosophical assumptions, foundations, and implications of mathematics. The aim of the philosophy of mathematics is to provide an account of the nature and methodology of mathematics and to understand the place of...
especially in the context of Persian Mathematics and Persian philosophy with which most of the other Persian scientists and philosophers such as Avicenna
Avicenna
Abū ʿAlī al-Ḥusayn ibn ʿAbd Allāh ibn Sīnā , commonly known as Ibn Sīnā or by his Latinized name Avicenna, was a Persian polymath, who wrote almost 450 treatises on a wide range of subjects, of which around 240 have survived...
, Biruni, and Tusi
Nasir al-Din al-Tusi
Khawaja Muḥammad ibn Muḥammad ibn Ḥasan Ṭūsī , better known as Naṣīr al-Dīn al-Ṭūsī , was a Persian polymath and prolific writer: an astronomer, biologist, chemist, mathematician, philosopher, physician, physicist, scientist, theologian and Marja Taqleed...
are associated. There are at least three basic mathematical ideas of strong philosophical dimensions that can be associated with Khayyám.
- Mathematical order: From where does this order issue, and why does it correspond to the world of nature? His answer is in one of his philosophical "treatises on being". Khayyám's answer is that "the Divine Origin of all existence not only emanates wojud or being, by virtue of which all things gain reality, but It is the source of order that is inseparable from the very act of existence."
- The significance of postulates (i.e. axiom) in geometryGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and the necessity for the mathematician to rely upon philosophy and hence the importance of the relation of any particular science to prime philosophy. This is the philosophical background to Khayyám's total rejection of any attempt to "prove" the parallel postulateParallel postulateIn geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
, and in turn his refusal to bring motion into the attempt to prove this postulate, as had Ibn al-Haytham, because Khayyám associated motion with the world of matter, and wanted to keep it away from the purely intelligible and immaterial world of geometry. - Clear distinction made by Khayyám, on the basis of the work of earlier Persian philosophers such as AvicennaAvicennaAbū ʿAlī al-Ḥusayn ibn ʿAbd Allāh ibn Sīnā , commonly known as Ibn Sīnā or by his Latinized name Avicenna, was a Persian polymath, who wrote almost 450 treatises on a wide range of subjects, of which around 240 have survived...
, between natural bodies and mathematical bodies. The first is defined as a body that is in the category of substance and that stands by itself, and hence a subject of natural sciences, while the second, called "volumeVolumeVolume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
", is of the category of accidents (attributes) that do not subsist by themselves in the external world and hence is the concern of mathematics. Khayyám was very careful to respect the boundaries of each discipline, and criticized Ibn al-Haytham in his proof of the parallel postulate precisely because he had broken this rule and had brought a subject belonging to natural philosophy, that is, motion, which belongs to natural bodies, into the domain of geometry, which deals with mathematical bodies.
Legacy
- A lunar crater Omar KhayyamOmar Khayyam (crater)Omar Khayyam is a lunar crater that is located just beyond the northwestern limb of the Moon, on the far side from the Earth. It lies in a region of the surface that is sometimes brought into view of the Earth due to libration, and under favorable lighting it can be viewed from the edge...
was named after him in 1970. - A minor planetMinor planetAn asteroid group or minor-planet group is a population of minor planets that have a share broadly similar orbits. Members are generally unrelated to each other, unlike in an asteroid family, which often results from the break-up of a single asteroid...
called 3095 Omarkhayyam3095 Omarkhayyam3095 Omarkhayyam is an outer main-belt asteroid discovered on September 8, 1980 by L. Zhuravleva at Nauchnyj. This minor planet was named in honor of the Persian mathematician and astronomer Omar Khayyám.- External links :*...
, discovered by SovietSoviet UnionThe Soviet Union , officially the Union of Soviet Socialist Republics , was a constitutionally socialist state that existed in Eurasia between 1922 and 1991....
astronomer Lyudmila ZhuravlyovaLyudmila ZhuravlyovaLyudmila Vasilyevna Zhuravleva is a Soviet, Russian and Ukrainian astronomer.She works at the Crimean Astrophysical Observatory.She also serves as president...
in 1980, is named after him.
See also
- Astronomy in medieval Islam
- Mathematics in medieval Islam
- Nozhat al-MajalesNozhat al-MajalesNoz'hat al-Majāles is an anthology which contains around 4,100 Persian quatrains by some 300 poets of the 5th to 7th11th-13th centuries. The anthology was compiled around the middle of the 7th/13th century by the Persian poet Jamal al-Din Khalil Shirvani...
- Omar Khayyam (film)Omar Khayyam (film)Omar Khayyam is an American movie directed by William Dieterle, filmed in 1956 and released in 1957...
- The Keeper: The Legend of Omar KhayyamThe Keeper: The Legend of Omar KhayyamThe Keeper: The Legend of Omar Khayyam is an independently-released drama film about the life of the famous Persian intellectual Omar Khayyám. It was directed by Kayvan Mashayekh and stars Vanessa Redgrave and Moritz Bleibtreu...
External links
(PDF version)- Umar Khayyam, at the Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
- Khayyam's works in original Persian at Ganjoor Persian Library
- Khayyam in Tarikhema.ir
- Listen to The Rubáiyát of Omar Khayyám audiobook at LibriVoxLibriVoxLibriVox is an online digital library of free public domain audiobooks, read by volunteers and is probably, since 2007, the world's most prolific audiobook publisher...
- The illustrated Rubáiyát of Omar Khayyám at Internet ArchiveInternet ArchiveThe Internet Archive is a non-profit digital library with the stated mission of "universal access to all knowledge". It offers permanent storage and access to collections of digitized materials, including websites, music, moving images, and nearly 3 million public domain books. The Internet Archive...
. - Omar Khayyam's Rubaiyat as translated by Edward Fitzgerald – 1st edition
- The Rubaiyat by Omar Khayyam – The Internet Classics Archive
- Illustrations to the Rubaiyat by Adelaide Hanscom

