A Saccheri quadrilateral is a quadrilateral

Quadrilateral

In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...

 with two equal sides perpendicular to the base. It is named after Giovanni Gerolamo Saccheri, who used it extensively in his book Euclid vindicatus (1733), an attempt to prove the parallel postulate

Parallel postulate

In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...

 using the method Reductio ad absurdum

Reductio ad absurdum

In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...

. The first known consideration of the Saccheri quadrilateral was by Omar Khayyam

Omar Khayyám

Omar Khayyám was aPersian polymath: philosopher, mathematician, astronomer and poet. He also wrote treatises on mechanics, geography, mineralogy, music, climatology and theology....

 in the late 11th century, and it may occasionally be referred to as the Khayyam-Saccheri quadrilateral.

For a Saccheri quadrilateral ABCD, the sides AD and BC (also called legs) are equal in length and perpendicular to the base AB. The top CD is called the summit or upper base and the angles at C and D are called the summit angles.

The advantage of using Saccheri quardrilaterals when considering the parallel postulate

Parallel postulate

In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...

 is that they place the mutually exclusive options in very clear terms:

Are the summit angles right angles, obtuse angles, or acute angles?

As it turns out, when the summit angles are right angles, this quadrilateral is equivalent to the statement expounded by Euclid's fifth postulate. When they are acute, this quadrilateral leads to hyperbolic geometry

Hyperbolic geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...

, and when they are obtuse, the quadrilateral leads to elliptical geometry. Saccheri himself, however, thought that both the obtuse and acute cases could be shown to be contradictory.

History

Saccheri quadrilaterals were first considered by Omar Khayyam

Omar Khayyám

Omar Khayyám was aPersian polymath: philosopher, mathematician, astronomer and poet. He also wrote treatises on mechanics, geography, mineralogy, music, climatology and theology....

 (1048-1131) in the late 11th century in Book I of Explanations of the Difficulties in the Postulates of Euclid. Unlike many commentators on Euclid before and after him (including of course Saccheri), Khayyam was not trying to prove the parallel postulate

Parallel postulate

In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...

 as such but to derive it from an equivalent postulate he formulated from "the principles of the Philosopher" (Aristotle

Aristotle

Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...

):

Two convergent straight lines intersect and it is impossible for two convergent straight lines to diverge in the direction in which they converge.

Khayyam then considered the three cases right, obtuse, and acute that the summit angles of a Saccheri quadrilateral can take and after proving a number of theorems about them, he (correctly) refuted the obtuse and acute cases based on his postulate and hence derived the classic postulate of Euclid.

It wasn't until 600 years later that Giordano Vitale made an advance on Khayyam in his book Euclide restituo (1680, 1686), when he used the quadrilateral to prove that if three points are equidistant on the base AB and the summit CD, then AB and CD are everywhere equidistant.

Saccheri himself based the whole of his long, heroic, and ultimately flawed proof of the parallel postulate around the quadrilateral and its three cases, proving many theorems about its properties along the way.

A formula

In the hyperbolic plane of constant curvature , the summit of a Saccheri quadrilateral can be calculated from the leg 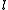and the base 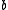using the formula.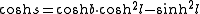