The hexagonal lattice or equilateral triangular lattice is one of the five 2D lattice

Lattice (group)

In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...

 types.

Three nearby points form an equilateral triangle. In images four orientations of such a triangle are by far the most common. They can conveniently be referred to, by viewing the triangle as an arrow, as pointing up, down, to the left, or to the right, although in each case they could also be considered to point into two oblique directions.

Two orientations of an image of the lattice are by far the most common. They can conveniently be referred to as "hexagonal lattice with horizontal rows" (like in the figure below), with triangles pointing up and down, and "hexagonal lattice with vertical rows", with triangles pointing left and right. They differ by an angle of 30°.

The hexagonal lattice with horizontal rows is a special case of a centered rectangular (i.e. rhombic) grid, with rectangles which are √3 times as high as wide. Of course for the other orientation the rectangles are √3 times as wide as high.

Its symmetry

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

 category is wallpaper group

Wallpaper group

A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...

 p6m. A pattern with this lattice of translational symmetry

Translational symmetry

In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...

 cannot have more, but may have less symmetry than the lattice itself.
For an image of a honeycomb

Honeycomb (geometry)

In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....

 structure, again two orientations are by far the most common. They can conveniently be referred to as "honeycomb structure with horizontal rows", with hexagons with two vertical sides, and "honeycomb structure with vertical rows", with hexagons with two horizontal sides. They differ by an angle of 90°, or equivalently 30°.

A honeycomb structure is in two ways related to a hexagonal lattice:

• the centers of the hexagons of a honeycomb form a hexagonal lattice, with the rows oriented the same
• the vertices of a honeycomb, together with their centers, form a hexagonal lattice, rotated by 30° (or equivalently 90°), and scaled by a factor 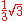, relative to the other lattice

The ratio of the number of vertices and the number of hexagons is 2, so together with the centers the ratio is 3, the reciprocal of the square of the scale factor.

The term honeycomb lattice could mean a corresponding hexagonal lattice, or a structure which is not a lattice in the group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

 sense, but e.g. one in the sense of a lattice model. A set of points forming the vertices of a honeycomb (without points at the centers) shows the honeycomb structure:
* * * * *
* * * * *
* * * * *
* * * * *
* * * * *
In addition to these points, or instead of them, the sides of the hexagons may be shown; depending on application they may be called lattice bonds.

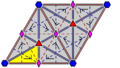
With respect to a hexagonal lattice we can distinguish two sets or three directions:

• the directions of the smallest distance between lattice points; let us call them the main translation directions
• the directions of the second smallest distance between lattice points; let us call them the secondary translation directions; these distances are √3 times as large. The set of lattice points can be partitioned into three sets with these larger translation distances.

Within each set of directions the directions differ by an angle of 60°, and between sets by angles of 30° and 90°. For a hexagonal lattice with horizontal rows one of the three directions is horizontal, and for a hexagonal lattice with vertical rows one of the three directions is vertical.

Conversely, for a given lattice we can create a rotated lattice that is √3 times as fine by adding the centers of the equilateral triangles. Since there are twice as many triangles as vertices, this triples the number of vertices.
A pattern with 3- or 6-fold rotational symmetry

Rotational symmetry

Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...

 has a lattice of 3-fold rotocenters (including possible 6-fold rotocenters) that is this finer lattice relative to the lattice of translational symmetry

Translational symmetry

In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...

.

In the case of 6-fold rotational symmetry the 6-fold centers form a lattice as coarse as the lattice of translational symmetry, i.e. there is one 6-fold center and there are two 3-fold centers per primitive cell.

For reflection axes, there are two possible sets of directions, mentioned above. In the case of 3-fold symmetry either none (p3) or one of the two applies:

• p3m1 with reflection axes along the shortest connections between the rotocenters
• p31m in the main translation directions

In the 6-fold case either none (p6) or both (p6m) apply.

If there are reflection axes in the main translation directions, one of the three sets of rotocenters play a different role than the other two: these reflection axes pass through them. With p6 one set is special because of being 6-fold.

See also

• hexagonal tiling
• close-packing
  Close-packing
  In geometry, close-packing of equal spheres is a dense arrangement of congruent spheres in an infinite, regular arrangement . Carl Friedrich Gauss proved that the highest average density – that is, the greatest fraction of space occupied by spheres – that can be achieved by a regular lattice...
  
  
• symmetry combinations
• centered hexagonal number
  Centered hexagonal number
  A centered hexagonal number, or hex number, is a centered figurate number that represents a hexagon with a dot in the center and all other dots surrounding the center dot in a hexagonal lattice....
  
  
• Eisenstein integer
  Eisenstein integer
  In mathematics, Eisenstein integers , also known as Eulerian integers , are complex numbers of the formz = a + b\omega \,\!where a and b are integers and...
  
  
• Voronoi diagram
  Voronoi diagram
  In mathematics, a Voronoi diagram is a special kind of decomposition of a given space, e.g., a metric space, determined by distances to a specified family of objects in the space...
  
  
• Loewner's torus
  Loewner's torus inequality
  In differential geometry, Loewner's torus inequality is an inequality due to Charles Loewner. It relates the systole and the area of an arbitrary Riemannian metric on the 2-torus.-Statement:...