
Hurwitz quaternion order
Encyclopedia
The Hurwitz quaternion order is a specific order in a quaternion algebra
over a suitable number field. The order is of particular importance in Riemann surface
theory, in connection with surfaces with maximal symmetry
, namely the Hurwitz surface
s. The Hurwitz quaternion order was studied in 1967 by Goro Shimura
, but first explicitly described by Noam Elkies
in 1998. For an alternative use of the term, see Integer quaternion (both usages are current in the literature).
 be the maximal real subfield of
be the maximal real subfield of 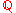
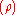 where
where 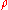 is a 7th-primitive root of unity
is a 7th-primitive root of unity
.
The ring of integers
of is
is 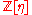 , where the element
, where the element 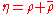 can be identified with the positive real
can be identified with the positive real  . Let
. Let  be the quaternion algebra
be the quaternion algebra
, or symbol algebra
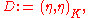
so that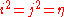 and
and 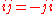 in
in  Also let
Also let  and
and 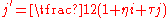 . Let
. Let
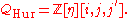
Then is a maximal order of
is a maximal order of  , described explicitly by Noam Elkies
, described explicitly by Noam Elkies
.
 is also generated by elements
is also generated by elements

and
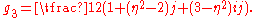
In fact, the order is a free -module over
-module over
the basis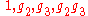 . Here the generators satisfy the relations
. Here the generators satisfy the relations

which descend to the appropriate relations in the (2,3,7) triangle group
, after quotienting by the center.
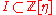 is by definition the group
is by definition the group
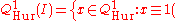 mod
mod 
namely, the group of elements of reduced norm 1 in equivalent to 1 modulo the ideal
equivalent to 1 modulo the ideal  . The corresponding Fuchsian group is obtained as the image of the principal congruence subgroup under a representation to PSL(2,R).
. The corresponding Fuchsian group is obtained as the image of the principal congruence subgroup under a representation to PSL(2,R).
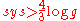 where g is the genus, improving an earlier result of Peter Buser and Peter Sarnak
where g is the genus, improving an earlier result of Peter Buser and Peter Sarnak
; see systoles of surfaces
.
Quaternion algebra
In mathematics, a quaternion algebra over a field F is a central simple algebra A over F that has dimension 4 over F. Every quaternion algebra becomes the matrix algebra by extending scalars , i.e...
over a suitable number field. The order is of particular importance in Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
theory, in connection with surfaces with maximal symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
, namely the Hurwitz surface
Hurwitz surface
In Riemann surface theory and hyperbolic geometry, a Hurwitz surface, named after Adolf Hurwitz, is a compact Riemann surface with preciselyautomorphisms, where g is the genus of the surface. This number is maximal by virtue of Hurwitz's theorem on automorphisms...
s. The Hurwitz quaternion order was studied in 1967 by Goro Shimura
Goro Shimura
is a Japanese mathematician, and currently a professor emeritus of mathematics at Princeton University.Shimura was a colleague and a friend of Yutaka Taniyama...
, but first explicitly described by Noam Elkies
Noam Elkies
Noam David Elkies is an American mathematician and chess master.At age 14, Elkies received a gold medal with a perfect score at the International Mathematical Olympiad, the youngest ever to do so...
in 1998. For an alternative use of the term, see Integer quaternion (both usages are current in the literature).
Definition
Let be the maximal real subfield of
be the maximal real subfield of 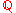
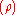 where
where 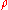 is a 7th-primitive root of unity
is a 7th-primitive root of unityRoot of unity
In mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
.
The ring of integers
Ring of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
of
 is
is 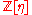 , where the element
, where the element 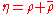 can be identified with the positive real
can be identified with the positive real  . Let
. Let  be the quaternion algebra
be the quaternion algebraQuaternion algebra
In mathematics, a quaternion algebra over a field F is a central simple algebra A over F that has dimension 4 over F. Every quaternion algebra becomes the matrix algebra by extending scalars , i.e...
, or symbol algebra
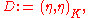
so that
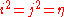 and
and 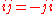 in
in  Also let
Also let  and
and 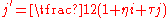 . Let
. Let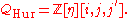
Then
 is a maximal order of
is a maximal order of  , described explicitly by Noam Elkies
, described explicitly by Noam ElkiesNoam Elkies
Noam David Elkies is an American mathematician and chess master.At age 14, Elkies received a gold medal with a perfect score at the International Mathematical Olympiad, the youngest ever to do so...
.
Module structure
The order is also generated by elements
is also generated by elements
and
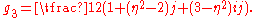
In fact, the order is a free
 -module over
-module overthe basis
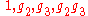 . Here the generators satisfy the relations
. Here the generators satisfy the relations
which descend to the appropriate relations in the (2,3,7) triangle group
(2,3,7) triangle group
In the theory of Riemann surfaces and hyperbolic geometry, the triangle group is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84, of its automorphism group.A note on terminology – the "...
, after quotienting by the center.
Principal congruence subgroups
The principal congruence subgroup defined by an ideal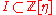 is by definition the group
is by definition the group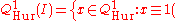 mod
mod 
namely, the group of elements of reduced norm 1 in
 equivalent to 1 modulo the ideal
equivalent to 1 modulo the ideal  . The corresponding Fuchsian group is obtained as the image of the principal congruence subgroup under a representation to PSL(2,R).
. The corresponding Fuchsian group is obtained as the image of the principal congruence subgroup under a representation to PSL(2,R).Application
The order was used by Katz, Schaps, and Vishne to construct a family of Hurwitz surfaces satsifying an asymptotic lower bound for the systole: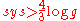 where g is the genus, improving an earlier result of Peter Buser and Peter Sarnak
where g is the genus, improving an earlier result of Peter Buser and Peter SarnakPeter Sarnak
Peter Clive Sarnak is a South African-born mathematician. He has been Eugene Higgins Professor of Mathematics at Princeton University since 2002, succeeding Andrew Wiles, and is an editor of the Annals of Mathematics...
; see systoles of surfaces
Systoles of surfaces
In mathematics, systolic inequalities for curves on surfaces were first studied by Charles Loewner in 1949 . Given a closed surface, its systole, denoted sys, is defined to the least length of a loop that cannot be contracted to a point on the surface. The systolic area of a metric is defined to...
.
See also
- (2,3,7) triangle group(2,3,7) triangle groupIn the theory of Riemann surfaces and hyperbolic geometry, the triangle group is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84, of its automorphism group.A note on terminology – the "...
- Klein quarticKlein quarticIn hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed...
- Macbeath surfaceMacbeath surfaceIn Riemann surface theory and hyperbolic geometry, the Macbeath surface, also called Macbeath's curve or the Fricke–Macbeath curve, is the genus-7 Hurwitz surface....
- First Hurwitz tripletFirst Hurwitz tripletIn the mathematical theory of Riemann surfaces, the first Hurwitz triplet is a triple of distinct Hurwitz surfaces with the identical automorphism group of the lowest possible genus, namely 14 . The explanation for this phenomenon is arithmetic...

