Systoles of surfaces
Encyclopedia
In mathematics
, systolic inequalities for curves on surfaces were first studied by Charles Loewner
in 1949 (unpublished; see remark at end of P. M. Pu's paper in '52). Given a closed surface, its systole, denoted sys, is defined to the least length of a loop that cannot be contracted to a point on the surface. The systolic area of a metric is defined to be the ratio area/sys2. The systolic ratio SR is the reciprocal quantity sys2/area. See also Introduction to systolic geometry
.
In 1949 Loewner proved his inequality
for metrics on the torus
T2, namely that the systolic ratio SR(T2) is bounded above by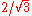
, with equality in the flat (constant curvature) case of the equilateral torus (see hexagonal lattice
).
, with an upper bound of π/2 for the systolic ratio SR(RP2), also attained in the constant curvature case.
For the Klein bottle
K, Bavard (1986) obtained an optimal upper bound of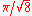
for the systolic ratio:
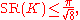
based on work by Blatter from the 1960s.
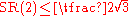, see (Katz-Sabourau '06). It is unknown whether or not every surface of positive genus satisfies Loewner's bound. It is conjectured that they all do. The answer is affirmative for genus 20 and above by (Katz-Sabourau '05).
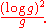
A similar lower bound (with a smaller constant) was obtained by Buser and Sarnak. Namely, they exhibited arithmetic hyperbolic Riemann surfaces with systole behaving as a constant times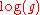
. Note that area is 4π(g-1) from the Gauss-Bonnet theorem, so that SR(g) behaves asymptotically as a constant times 
.
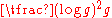The study of the asymptotic behavior for large genus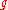
of the systole of hyperbolic surfaces reveals some interesting constants. Thus, Hurwitz surface
s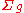
defined by a tower of principal congruence subgroups of the (2,3,7) hyperbolic triangle group
satisfy the bound
resulting from an analysis of the Hurwitz quaternion order
. A similar bound holds for more general arithmetic Fuchsian group
s. This 2007 result by Mikhail Katz
, Mary Schaps, and Uzi Vishne improves an inequality due to Peter Sarnak
and Peter Buser in the case of arithmetic groups defined over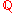
, from 1994, which contained a nonzero additive constant. For the Hurwitz surfaces of principal congruence type, the systolic ratio SR(g) is asymptotic to
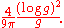
Using Katok's entropy inequality, the following asymptotic upper bound for SR(g) was found in (Katz-Sabourau 2005):
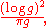
see also (Katz 2007), p. 85. Combining the two estimates, one obtains tight bounds for the asymptotic behavior of the systolic ratio of surfaces.
for the ratio area/L2. A lower bound of 1/961 obtained by Croke in '88 has recently been improved by Nabutovsky, Rotman, and Sabourau.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, systolic inequalities for curves on surfaces were first studied by Charles Loewner
Charles Loewner
Charles Loewner was an American mathematician. His name was Karel Löwner in Czech and Karl Löwner in German.Loewner received his Ph.D...
in 1949 (unpublished; see remark at end of P. M. Pu's paper in '52). Given a closed surface, its systole, denoted sys, is defined to the least length of a loop that cannot be contracted to a point on the surface. The systolic area of a metric is defined to be the ratio area/sys2. The systolic ratio SR is the reciprocal quantity sys2/area. See also Introduction to systolic geometry
Introduction to systolic geometry
Systolic geometry is a branch of differential geometry, a field within mathematics, studying problems such as the relationship between the area inside a closed curve C, and the length or perimeter of C. Since the area A may be small while the length l is large, when C looks elongated, the...
.
Torus
Loewner's torus inequality
In differential geometry, Loewner's torus inequality is an inequality due to Charles Loewner. It relates the systole and the area of an arbitrary Riemannian metric on the 2-torus.-Statement:...
for metrics on the torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
T2, namely that the systolic ratio SR(T2) is bounded above by
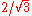, with equality in the flat (constant curvature) case of the equilateral torus (see hexagonal latticeHexagonal lattice
The hexagonal lattice or equilateral triangular lattice is one of the five 2D lattice types.Three nearby points form an equilateral triangle. In images four orientations of such a triangle are by far the most common...
).
Real projective plane
A similar result is given by Pu's inequality for the real projective plane from 1952, due to Pao Ming PuPao Ming Pu
Pao Ming Pu Pao Ming Pu Pao Ming Pu (the form of his name he used in Western languages, although the Wade-Giles transliteration would be Pu Baoming; ; Aug. 1910– Feb...
, with an upper bound of π/2 for the systolic ratio SR(RP2), also attained in the constant curvature case.
Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
K, Bavard (1986) obtained an optimal upper bound of
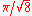for the systolic ratio: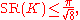based on work by Blatter from the 1960s.
Genus 2
An orientable surface of genus 2 satisfies Loewner's bound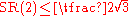, see (Katz-Sabourau '06). It is unknown whether or not every surface of positive genus satisfies Loewner's bound. It is conjectured that they all do. The answer is affirmative for genus 20 and above by (Katz-Sabourau '05).Arbitrary genus
For a closed surface of genus g, Hebda and Burago (1980) showed that the systolic ratio SR(g) is bounded above by the constant 2. Three years later, Mikhail Gromov found an upper bound for SR(g) given by a constant times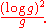A similar lower bound (with a smaller constant) was obtained by Buser and Sarnak. Namely, they exhibited arithmetic hyperbolic Riemann surfaces with systole behaving as a constant times
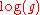. Note that area is 4π(g-1) from the Gauss-Bonnet theorem, so that SR(g) behaves asymptotically as a constant times 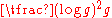.The study of the asymptotic behavior for large genus
of the systole of hyperbolic surfaces reveals some interesting constants. Thus, Hurwitz surfaceHurwitz surface
In Riemann surface theory and hyperbolic geometry, a Hurwitz surface, named after Adolf Hurwitz, is a compact Riemann surface with preciselyautomorphisms, where g is the genus of the surface. This number is maximal by virtue of Hurwitz's theorem on automorphisms...
s
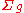defined by a tower of principal congruence subgroups of the (2,3,7) hyperbolic triangle group(2,3,7) triangle group
In the theory of Riemann surfaces and hyperbolic geometry, the triangle group is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84, of its automorphism group.A note on terminology – the "...
satisfy the bound
resulting from an analysis of the Hurwitz quaternion order
Hurwitz quaternion order
The Hurwitz quaternion order is a specific order in a quaternion algebra over a suitable number field. The order is of particular importance in Riemann surface theory, in connection with surfaces with maximal symmetry, namely the Hurwitz surfaces. The Hurwitz quaternion order was studied in 1967...
. A similar bound holds for more general arithmetic Fuchsian group
Fuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
s. This 2007 result by Mikhail Katz
Mikhail Katz
Mikhail Katz is an Israeli mathematician, a professor of mathematics at Bar Ilan University. His main interests are differential geometry and geometric topology; he is the author of a book about systolic geometry....
, Mary Schaps, and Uzi Vishne improves an inequality due to Peter Sarnak
Peter Sarnak
Peter Clive Sarnak is a South African-born mathematician. He has been Eugene Higgins Professor of Mathematics at Princeton University since 2002, succeeding Andrew Wiles, and is an editor of the Annals of Mathematics...
and Peter Buser in the case of arithmetic groups defined over
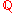, from 1994, which contained a nonzero additive constant. For the Hurwitz surfaces of principal congruence type, the systolic ratio SR(g) is asymptotic to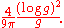Using Katok's entropy inequality, the following asymptotic upper bound for SR(g) was found in (Katz-Sabourau 2005):
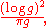
see also (Katz 2007), p. 85. Combining the two estimates, one obtains tight bounds for the asymptotic behavior of the systolic ratio of surfaces.
Sphere
There is also a version of the inequality for metrics on the sphere, for the invariant L defined as the least length of a closed geodesic of the metric. In '80, Gromov conjectured a lower bound of for the ratio area/L2. A lower bound of 1/961 obtained by Croke in '88 has recently been improved by Nabutovsky, Rotman, and Sabourau.