Introduction to systolic geometry
Encyclopedia
Systolic geometry is a branch of differential geometry, a field within mathematics, studying problems such as the relationship between the area
inside a closed curve C, and the length
or perimeter of C. Since the area A may be small while the length l is large, when C looks elongated, the relationship can only take the form of an inequality. What is more, such an inequality would be an upper bound
for A: there is no interesting lower bound just in terms of the length.
Mikhail Gromov once voiced the opinion that the isoperimetric inequality was known already to the Ancient Greeks. The mythological tale of Dido, Queen of Carthage shows that problems about making a maximum area for a given perimeter were posed in a natural way, in past eras.
The relation between length and area is closely related to the physical phenomenon known as surface tension
, which gives a visible form to the comparable relation between surface area
and volume
. The familiar shapes of drops of water express minima of surface area.
The purpose of this article is to explain another such relation between length and area. A space is called simply connected if every loop in the space can be contracted to a point in a continuous fashion. For example, a room with a pillar in the middle, connecting floor to ceiling, is not simply connected. In geometry
, a systole is a distance which is characteristic of a compact metric space
which is not simply connected. It is the length of a shortest loop in the space that cannot be contracted to a point in the space. Systolic geometry gives lower bounds for various attributes of the space in terms of its systole.
It is known that the Fubini-Study metric
is the natural metric for the geometrisation of quantum mechanics. In an intriguing connection to global geometric phenomena, it turns out that the Fubini-Study metric can be characterized as the boundary case of equality in Gromov's inequality for complex projective space, involving an area
quantity called the 2-systole, pointing to a possible connection to quantum mechanical phenomena.
In the following, these systolic inequalities will be compared to the classical isoperimetric inequalities, which can in turn be motivated by physical phenomena observed in the behavior of a water drop.
Perhaps the most familiar physical manifestation of the 3-dimensional isoperimetric inequality is the shape of a drop of water. Namely, a drop will typically assume a symmetric round shape. Since the amount of water in a drop is fixed, surface tension forces the drop into a shape which minimizes the surface area of the drop, namely a round sphere. Thus the round shape of the drop is a consequence of the phenomenon of surface tension. Mathematically, this phenomenon is expressed by the isoperimetric inequality.
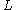of a closed curve and the area 
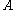of the planar region that it encloses. The isoperimetric inequality states that
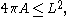
and that the equality holds if and only if the curve is a round circle. The inequality is an upper bound for area in terms of length. It can be rewritten as follows:
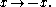
Thus, in the plane central symmetry is the rotation by 180 degrees. For example, an ellipse is centrally symmetric, as is any ellipsoid in 3-space.
Any centrally symmetric convex body of surface area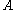
can be squeezed through a noose of length 
, with the tightest fit achieved by a sphere. This property is equivalent to a special case of Pu's inequality, one of the earliest systolic inequalities.
For example, an ellipsoid is an example of a convex centrally symmetric body in 3-space. It may be helpful to the reader to develop an intuition for the property mentioned above in the context of thinking about ellipsoidal examples.
An alternative formulation is as follows. Every convex centrally symmetric body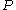
in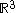 
admits a pair of opposite (antipodal) points and a path of length
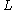joining them and lying on the boundary 
of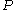 
, satisfying
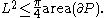
The systole of a compact metric space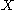 
is a metric
invariant of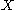
, defined to be the least length of a
noncontractible loop in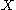
. We will denote it as follows:
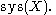
Note that a loop minimizing length is necessarily a closed geodesic
. When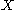
is a graph
, the invariant is usually referred to as the girth, ever since the 1947 article by William Tutte. Possibly inspired by Tutte's article, Charles Loewner
started thinking about systolic questions on surfaces in the late 1940s, resulting in a 1950 thesis by his student P. M. Pu. The actual term systole itself was not coined until a quarter century later, by Marcel Berger
.
This line of research was, apparently, given further impetus by a remark of René Thom
, in a conversation with Berger in the library of Strasbourg University during the 1961-62 academic year, shortly after the publication of the papers of R. Accola and C. Blatter. Referring to these systolic inequalities, Thom reportedly exclaimed: Mais c'est fondamental! [These results are of fundamental importance!]
Subsequently, Berger popularized the subject in a series of articles and books, most recently in the march '08 issue of the Notices of the American Mathematical Society
. A bibliography at the Website for systolic geometry and topology currently contains over 170 articles. Systolic geometry is a rapidly developing field, featuring a number of recent publications in leading journals. Recently, an intriguing link has emerged with the Lusternik-Schnirelmann category. The existence of such a link can be thought of as a theorem in systolic topology.
In projective geometry
, the real projective plane
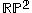is defined as the collection of lines through the origin in 
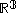. The distance function on 
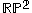is most readily understood from this point of view. Namely, the distance between two lines through the origin is by definition the angle between them (measured in radians), or more precisely the lesser of the two angles. This distance function corresponds to the metric of constant Gaussian curvature
+1.
Alternatively,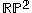
can be defined as the surface obtained by identifying each pair of antipodal points on the 2-sphere.
Other metrics on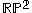
can be obtained by quotienting metrics on 
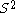imbedded in 3-space in a centrally symmetric way.
Topologically,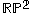
can be obtained from the Mobius strip by attaching a disk along the boundary.
Among closed surfaces, the real projective plane is the simplest non-orientable such surface.
.
A student of Charles Loewner
's, Pao Ming Pu
proved in a 1950 thesis (published in 1952) that every metric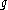
on the real projective plane 
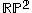satisfies the optimal inequality
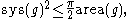
where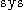
is the systole. The boundary case of equality is attained precisely when the metric is of constant Gaussian curvature. Alternatively, the inequality can be presented as follows:
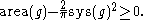
There is a vast generalisation of Pu's inequality, due to Mikhail Gromov, called Gromov's systolic inequality for essential manifolds
. To state his result, one requires a topological notion of an essential manifold
.
Similarly to Pu's inequality, Loewner's torus inequality
relates
the total area, to the systole, i.e. least length of a noncontractible
loop on the torus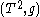
:
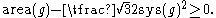
The boundary case of equality is attained if and only if the metric is
homothetic to the flat metric obtained as the quotient of
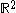by the lattice formed by the
Eisenstein integers.
is the strengthened
isoperimetric inequality
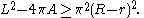
Here
is the area of the region bounded by a closed Jordan curve of length (perimeter) 
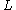in the plane, 
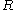is the circumradius of the bounded region, and 
is its inradius. The error term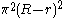 
on the right hand side is traditionally called the isoperimetric defect. There exists a similar strengthening of Loewner's inequality.
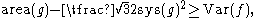
where Var is the probabilistic variance
while f is the conformal factor expressing the metric g in terms of the flat metric of unit area in the conformal class of g. The proof results from a combination of the computational formula for the variance and Fubini's theorem
(see Horowitz et al, 2009).
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
inside a closed curve C, and the length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
or perimeter of C. Since the area A may be small while the length l is large, when C looks elongated, the relationship can only take the form of an inequality. What is more, such an inequality would be an upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
for A: there is no interesting lower bound just in terms of the length.
Mikhail Gromov once voiced the opinion that the isoperimetric inequality was known already to the Ancient Greeks. The mythological tale of Dido, Queen of Carthage shows that problems about making a maximum area for a given perimeter were posed in a natural way, in past eras.
The relation between length and area is closely related to the physical phenomenon known as surface tension
Surface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
, which gives a visible form to the comparable relation between surface area
Surface area
Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
and volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
. The familiar shapes of drops of water express minima of surface area.
The purpose of this article is to explain another such relation between length and area. A space is called simply connected if every loop in the space can be contracted to a point in a continuous fashion. For example, a room with a pillar in the middle, connecting floor to ceiling, is not simply connected. In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a systole is a distance which is characteristic of a compact metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
which is not simply connected. It is the length of a shortest loop in the space that cannot be contracted to a point in the space. Systolic geometry gives lower bounds for various attributes of the space in terms of its systole.
It is known that the Fubini-Study metric
Fubini-Study metric
In mathematics, the Fubini–Study metric is a Kähler metric on projective Hilbert space, that is, complex projective space CPn endowed with a Hermitian form. This metric was originally described in 1904 and 1905 by Guido Fubini and Eduard Study....
is the natural metric for the geometrisation of quantum mechanics. In an intriguing connection to global geometric phenomena, it turns out that the Fubini-Study metric can be characterized as the boundary case of equality in Gromov's inequality for complex projective space, involving an area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
quantity called the 2-systole, pointing to a possible connection to quantum mechanical phenomena.
In the following, these systolic inequalities will be compared to the classical isoperimetric inequalities, which can in turn be motivated by physical phenomena observed in the behavior of a water drop.
Surface tension and shape of a water drop
Isoperimetric inequality in the plane
The solution to the isoperimetric problem in the plane is usually expressed in the form of an inequality that relates the length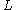 of a closed curve and the area 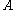of the planar region that it encloses. The isoperimetric inequality states that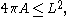and that the equality holds if and only if the curve is a round circle. The inequality is an upper bound for area in terms of length. It can be rewritten as follows:
Central symmetry
Recall the notion of central symmetry: a Euclidean polyhedron is called centrally symmetric if it is invariant under the antipodal map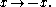Thus, in the plane central symmetry is the rotation by 180 degrees. For example, an ellipse is centrally symmetric, as is any ellipsoid in 3-space.
Property of a centrally symmetric polyhedron in 3-space
There is a geometric inequality that is in a sense dual to the isoperimetric inequality in the following sense. Both involve a length and an area. The isoperimetric inequality is an upper bound for area in terms of length. There is a geometric inequality which provides an upper bound for a certain length in terms of area. More precisely it can be described as follows.Any centrally symmetric convex body of surface area
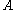can be squeezed through a noose of length , with the tightest fit achieved by a sphere. This property is equivalent to a special case of Pu's inequality, one of the earliest systolic inequalities.For example, an ellipsoid is an example of a convex centrally symmetric body in 3-space. It may be helpful to the reader to develop an intuition for the property mentioned above in the context of thinking about ellipsoidal examples.
An alternative formulation is as follows. Every convex centrally symmetric body
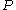in 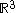admits a pair of opposite (antipodal) points and a path of length 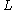joining them and lying on the boundary of 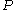, satisfying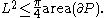Notion of systole
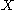is a metricinvariant of
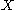, defined to be the least length of anoncontractible loop in
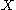. We will denote it as follows: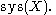Note that a loop minimizing length is necessarily a closed geodesic
Closed geodesic
In differential geometry and dynamical systems, a closed geodesic on a Riemannian manifold M is the projection of a closed orbit of the geodesic flow on M.-Examples:On the unit sphere, every great circle is an example of a closed geodesic...
. When
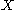is a graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
, the invariant is usually referred to as the girth, ever since the 1947 article by William Tutte. Possibly inspired by Tutte's article, Charles Loewner
Charles Loewner
Charles Loewner was an American mathematician. His name was Karel Löwner in Czech and Karl Löwner in German.Loewner received his Ph.D...
started thinking about systolic questions on surfaces in the late 1940s, resulting in a 1950 thesis by his student P. M. Pu. The actual term systole itself was not coined until a quarter century later, by Marcel Berger
Marcel Berger
Marcel Berger is a French mathematician, doyen of French differential geometry, and a former director of the Institut des Hautes Études Scientifiques , France...
.
This line of research was, apparently, given further impetus by a remark of René Thom
René Thom
René Frédéric Thom was a French mathematician. He made his reputation as a topologist, moving on to aspects of what would be called singularity theory; he became world-famous among the wider academic community and the educated general public for one aspect of this latter interest, his work as...
, in a conversation with Berger in the library of Strasbourg University during the 1961-62 academic year, shortly after the publication of the papers of R. Accola and C. Blatter. Referring to these systolic inequalities, Thom reportedly exclaimed: Mais c'est fondamental! [These results are of fundamental importance!]
Subsequently, Berger popularized the subject in a series of articles and books, most recently in the march '08 issue of the Notices of the American Mathematical Society
Notices of the American Mathematical Society
Notices of the American Mathematical Society is a membership magazine of the American Mathematical Society, published monthly except for the combined June/July issue. It is the world's most widely read mathematics magazine, sent to the approximately 30,000 AMS members worldwide...
. A bibliography at the Website for systolic geometry and topology currently contains over 170 articles. Systolic geometry is a rapidly developing field, featuring a number of recent publications in leading journals. Recently, an intriguing link has emerged with the Lusternik-Schnirelmann category. The existence of such a link can be thought of as a theorem in systolic topology.
The real projective plane
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
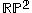is defined as the collection of lines through the origin in 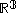. The distance function on 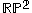is most readily understood from this point of view. Namely, the distance between two lines through the origin is by definition the angle between them (measured in radians), or more precisely the lesser of the two angles. This distance function corresponds to the metric of constant Gaussian curvatureGaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
+1.
Alternatively,
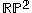can be defined as the surface obtained by identifying each pair of antipodal points on the 2-sphere.Other metrics on
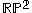can be obtained by quotienting metrics on 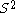imbedded in 3-space in a centrally symmetric way.Topologically,
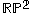can be obtained from the Mobius strip by attaching a disk along the boundary.Among closed surfaces, the real projective plane is the simplest non-orientable such surface.
Pu's inequality
Pu's inequality for the real projective plane applies to general Riemannian metrics on.A student of Charles Loewner
Charles Loewner
Charles Loewner was an American mathematician. His name was Karel Löwner in Czech and Karl Löwner in German.Loewner received his Ph.D...
's, Pao Ming Pu
Pao Ming Pu
Pao Ming Pu Pao Ming Pu Pao Ming Pu (the form of his name he used in Western languages, although the Wade-Giles transliteration would be Pu Baoming; ; Aug. 1910– Feb...
proved in a 1950 thesis (published in 1952) that every metric
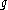on the real projective plane 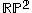satisfies the optimal inequality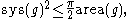where
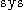is the systole. The boundary case of equality is attained precisely when the metric is of constant Gaussian curvature. Alternatively, the inequality can be presented as follows: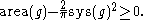There is a vast generalisation of Pu's inequality, due to Mikhail Gromov, called Gromov's systolic inequality for essential manifolds
Gromov's systolic inequality for essential manifolds
In the mathematical field of Riemannian geometry, M. Gromov's systolic inequality bounds the length of the shortest non-contractible loop on a Riemannian manifold in terms of the volume of the manifold...
. To state his result, one requires a topological notion of an essential manifold
Essential manifold
In mathematics, in algebraic topology and differential geometry, the notion of an essential manifold seems to have been first introduced explicitly in Mikhail Gromov's classic text in 1983 .-Definition:...
.
Loewner's torus inequality
Loewner's torus inequality
In differential geometry, Loewner's torus inequality is an inequality due to Charles Loewner. It relates the systole and the area of an arbitrary Riemannian metric on the 2-torus.-Statement:...
relates
the total area, to the systole, i.e. least length of a noncontractible
loop on the torus
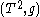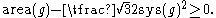
:The boundary case of equality is attained if and only if the metric is
homothetic to the flat metric obtained as the quotient of
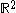by the lattice formed by theEisenstein integers.
Bonnesen's inequality
The classical Bonnesen's inequalityBonnesen's inequality
Bonnesen's inequality is an inequality relating the length, the area, the radius of the incircle and the radius of the circumcircle of a Jordan curve. It is a strengthening of the classical isoperimetric inequality....
is the strengthened
isoperimetric inequality
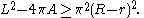
Here
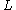is the area of the region bounded by a closed Jordan curve of length (perimeter) in the plane, 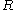is the circumradius of the bounded region, and is its inradius. The error term 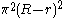on the right hand side is traditionally called the isoperimetric defect. There exists a similar strengthening of Loewner's inequality.Loewner's inequality with a defect term
The explanation of the strengthened version of Loewner's inequality is somewhat more technical than the rest of this article. It seems worth including it here for the sake of completeness. The strengthened version is the inequality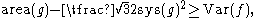where Var is the probabilistic variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
while f is the conformal factor expressing the metric g in terms of the flat metric of unit area in the conformal class of g. The proof results from a combination of the computational formula for the variance and Fubini's theorem
Fubini's theorem
In mathematical analysis Fubini's theorem, named after Guido Fubini, is a result which gives conditions under which it is possible to compute a double integral using iterated integrals. As a consequence it allows the order of integration to be changed in iterated integrals.-Theorem...
(see Horowitz et al, 2009).