
Closed geodesic
Encyclopedia
In differential geometry and dynamical systems, a closed geodesic on a Riemannian manifold
M is the projection of a closed orbit of the geodesic flow on M.
, every great circle is an example of a closed geodesic. On a compact hyperbolic surface
, closed geodesics are in one-to-one correspondence with non-trivial conjugacy class
es of elements in the Fuchsian group
of the surface. A prime geodesic
is an example of a closed geodesic.
is an -action
-action
on tangent bundle
T(M) of a manifold M defined in the following way
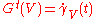
where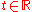 ,
,  and
and 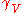 denotes the geodesic with initial data
denotes the geodesic with initial data  .
.
It defines a Hamiltonian flow on (co)tangent bundle with the (pseudo-)Riemannian metric as the Hamiltonian
. In particular it preserves the (pseudo-)Riemannian metric , i.e.
, i.e.
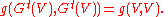
That makes possible to define geodesic flow on unit tangent bundle
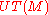 of the Riemannian manifold
of the Riemannian manifold  when the geodesic
when the geodesic 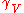 is of unit speed.
is of unit speed.
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
M is the projection of a closed orbit of the geodesic flow on M.
Examples
On the unit sphereUnit sphere
In mathematics, a unit sphere is the set of points of distance 1 from a fixed central point, where a generalized concept of distance may be used; a closed unit ball is the set of points of distance less than or equal to 1 from a fixed central point...
, every great circle is an example of a closed geodesic. On a compact hyperbolic surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
, closed geodesics are in one-to-one correspondence with non-trivial conjugacy class
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
es of elements in the Fuchsian group
Fuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
of the surface. A prime geodesic
Prime geodesic
In mathematics, a prime geodesic on a hyperbolic surface is a primitive closed geodesic, i.e. a geodesic which is a closed curve that traces out its image exactly once...
is an example of a closed geodesic.
Definition
Geodesic flowFlow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
is an
 -action
-actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
T(M) of a manifold M defined in the following way
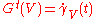
where
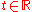 ,
,  and
and 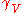 denotes the geodesic with initial data
denotes the geodesic with initial data  .
.It defines a Hamiltonian flow on (co)tangent bundle with the (pseudo-)Riemannian metric as the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
. In particular it preserves the (pseudo-)Riemannian metric
 , i.e.
, i.e.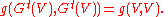
That makes possible to define geodesic flow on unit tangent bundle
Unit tangent bundle
In Riemannian geometry, a branch of mathematics, the unit tangent bundle of a Riemannian manifold , denoted by UT or simply UTM, is the unit sphere bundle for the tangent bundle T...
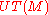 of the Riemannian manifold
of the Riemannian manifold  when the geodesic
when the geodesic 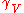 is of unit speed.
is of unit speed.

