
Essential manifold
Encyclopedia
In mathematics
, in algebraic topology
and differential geometry, the notion of an essential manifold seems to have been first introduced explicitly in Mikhail Gromov's classic text in 1983 (see below).
M is called essential if its fundamental class
[M] defines a nonzero element in the homology
of its fundamental group
π, or more precisely in the homology of the corresponding Eilenberg–MacLane space K(π, 1), via the natural homomorphism ,
,
where n is the dimension of M. Here the fundamental class is taken in homology with integer coefficients if the manifold is orientable, and in coefficients modulo 2, otherwise.
Real projective space RPn is essential since the inclusion

is injective in homology, where
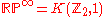
is the Eilenberg-MacLane space of the finite cyclic group of order 2.
Further examples of essential manifolds include aspherical manifolds and lens space
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
and differential geometry, the notion of an essential manifold seems to have been first introduced explicitly in Mikhail Gromov's classic text in 1983 (see below).
Definition
A closed manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M is called essential if its fundamental class
Fundamental class
In mathematics, the fundamental class is a homology class [M] associated to an oriented manifold M, which corresponds to "the whole manifold", and pairing with which corresponds to "integrating over the manifold"...
[M] defines a nonzero element in the homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
of its fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
π, or more precisely in the homology of the corresponding Eilenberg–MacLane space K(π, 1), via the natural homomorphism
 ,
,where n is the dimension of M. Here the fundamental class is taken in homology with integer coefficients if the manifold is orientable, and in coefficients modulo 2, otherwise.
Examples
All closed surfaces (i.e. 2-dimensional manifolds) are essential with the exception of the 2-sphere S2.Real projective space RPn is essential since the inclusion

is injective in homology, where
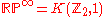
is the Eilenberg-MacLane space of the finite cyclic group of order 2.
Further examples of essential manifolds include aspherical manifolds and lens space
Lens space
A lens space is an example of a topological space, considered in mathematics. The term often refers to a specific class of 3-manifolds, but in general can be defined for higher dimensions....
s.
See also
- Gromov's systolic inequality for essential manifoldsGromov's systolic inequality for essential manifoldsIn the mathematical field of Riemannian geometry, M. Gromov's systolic inequality bounds the length of the shortest non-contractible loop on a Riemannian manifold in terms of the volume of the manifold...
- Systolic geometry

