Lens space
Encyclopedia
A lens space is an example of a topological space
, considered in mathematics
. The term often refers to a specific class of 3-manifold
s, but in general can be defined for higher dimensions.
In the 3-manifold case, a lens space can be visualized as the result of gluing two solid tori
together by a homeomorphism of their boundaries. Often the 3-sphere
and
, both of which can be obtained as above, are not counted as they are considered trivial special cases.
The three-dimensional lens spaces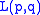
were introduced by Tietze
in 1908. They were the first known examples of 3-manifolds which were not determined by their homology
and fundamental group
alone, and the simplest examples of closed manifolds whose homeomorphism type is not determined by their homotopy type. J.W. Alexander in 1919 showed that the lens spaces
and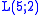 
were not homeomorphic even though they have isomorphic fundamental groups and the same homology, though they do not have the same homotopy type. Other lens spaces have the same homotopy type (and thus isomorphic fundamental groups and homology), but not the same homeomorphism type; they can thus can be seen as the birth of geometric topology
of manifolds as distinct from algebraic topology
.
There is a complete classification of three-dimensional lens spaces, by Reidemeister torsion.
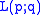are quotients of 
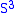by 
-actions. More precisely, let 
and 
be coprime
integers and consider
as the unit sphere in 
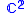. Then the 
-action on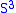 
generated by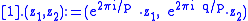
is free as p and q were coprime. The resulting quotient space is called the lens space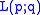
.
This can be generalized to higher dimensions as follows: Let
be integers such that the 
are coprime to 
and consider 
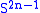as the unit sphere in 
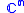. The lens space 
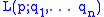is the quotient of 
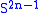by the free 
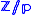-action generated by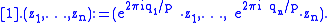
In three dimensions we have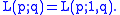
The fundamental group of all the lens space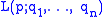s
is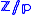 
independent of the 
.
.
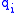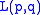Another related definition is to view the solid ball as the following solid bipyramid
: construct a planar regular p sided polygon
. Put two points n and s directly above and below the center of the polygon. Construct the bipyramid by joining each point of the regular p sided polygon to n and s. Fill in the bipyramid to make it solid and give the triangles on the boundary the same identification as above.
and
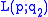are:
The invariant that gives the homotopy classification of 3-dimensional lens spaces is the torsion linking form.
The homeomorphism classification is more subtle, and is given by Reidemeister torsion. This was given in as a classification up to PL homeomorphism, but it was shown in to be a homeomorphism classification. In modern terms, lens spaces are determined by simple homotopy type, and there are no normal invariants (like characteristic classes) or surgery obstruction.
A knot-theoretic
classification is given in :
let C be a closed curve in the lens space which lifts to a knot in the universal cover of the lens space. If the lifted knot has a trivial Alexander polynomial
, compute the torsion linking form on the pair (C,C) – then this gives the homeomorphism classification.
Another invariant is the homotopy type of the configuration space
s – showed that homotopy equivalent but not homeomorphic lens spaces may have configuration spaces with different homotopy types, which can be detected by different Massey product
s.
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, considered in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. The term often refers to a specific class of 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s, but in general can be defined for higher dimensions.
In the 3-manifold case, a lens space can be visualized as the result of gluing two solid tori
Solid torus
In mathematics, a solid torus is a topological space homeomorphic to S^1 \times D^2, i.e. the cartesian product of the circle with a two dimensional disc endowed with the product topology. The solid torus is a connected, compact, orientable 3-dimensional manifold with boundary...
together by a homeomorphism of their boundaries. Often the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
and
, both of which can be obtained as above, are not counted as they are considered trivial special cases.The three-dimensional lens spaces
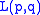were introduced by TietzeTietze
Tietze may refer to:* Alexander Tietze , German physician* Andreas Tietze* Emil Tietze , Austrian geologist; * Erica Tietze-Conrat , Austrian female art historian; * Friedel Tietze, German athlete...
in 1908. They were the first known examples of 3-manifolds which were not determined by their homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
and fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
alone, and the simplest examples of closed manifolds whose homeomorphism type is not determined by their homotopy type. J.W. Alexander in 1919 showed that the lens spaces
and 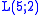were not homeomorphic even though they have isomorphic fundamental groups and the same homology, though they do not have the same homotopy type. Other lens spaces have the same homotopy type (and thus isomorphic fundamental groups and homology), but not the same homeomorphism type; they can thus can be seen as the birth of geometric topologyGeometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
of manifolds as distinct from algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
.
There is a complete classification of three-dimensional lens spaces, by Reidemeister torsion.
Definition
The three-dimensional lens spaces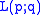 are quotients of 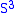by -actions. More precisely, let and be coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
integers and consider
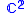as the unit sphere in . Then the -action on 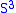generated by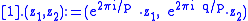is free as p and q were coprime. The resulting quotient space is called the lens space
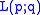.This can be generalized to higher dimensions as follows: Let
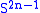be integers such that the are coprime to and consider as the unit sphere in 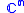. The lens space 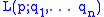is the quotient of 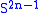by the free 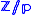-action generated by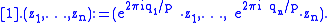In three dimensions we have
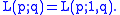
The fundamental group of all the lens spaces
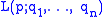is 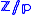independent of the 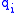.Alternative definitions of three-dimensional lens spaces
The three dimensional lens space L(p,q) is often defined to be a solid ball with the following identification: first mark p equidistant points on the equator of the solid ball, denote them a0 to ap-1, then on the boundary of the ball, draw geodesic lines connecting the points to the north and south pole. Now identify spherical triangles by identifying the north pole to the south pole and the points ai with ai+q and ai+1 with ai+q+1. The resulting space is homeomorphic to the lens space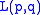.Another related definition is to view the solid ball as the following solid bipyramid
Bipyramid
An n-gonal bipyramid or dipyramid is a polyhedron formed by joining an n-gonal pyramid and its mirror image base-to-base.The referenced n-gon in the name of the bipyramids is not an external face but an internal one, existing on the primary symmetry plane which connects the two pyramid halves.The...
: construct a planar regular p sided polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
. Put two points n and s directly above and below the center of the polygon. Construct the bipyramid by joining each point of the regular p sided polygon to n and s. Fill in the bipyramid to make it solid and give the triangles on the boundary the same identification as above.
Classification of 3-dimensional lens spaces
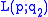Classifications up to homeomorphism and homotopy equivalence are known, as follows. The three-dimensional spaces and are:
- homotopy equivalent if and only if
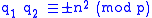for some 
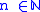; - homeomorphic if and only if
.
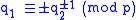- In this case they are "obviously" homeomorphic, as one can easily produce a homeomorphism. It is harder to show that these are the only homeomorphic lens spaces.
The invariant that gives the homotopy classification of 3-dimensional lens spaces is the torsion linking form.
The homeomorphism classification is more subtle, and is given by Reidemeister torsion. This was given in as a classification up to PL homeomorphism, but it was shown in to be a homeomorphism classification. In modern terms, lens spaces are determined by simple homotopy type, and there are no normal invariants (like characteristic classes) or surgery obstruction.
A knot-theoretic
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
classification is given in :
let C be a closed curve in the lens space which lifts to a knot in the universal cover of the lens space. If the lifted knot has a trivial Alexander polynomial
Alexander polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
, compute the torsion linking form on the pair (C,C) – then this gives the homeomorphism classification.
Another invariant is the homotopy type of the configuration space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
s – showed that homotopy equivalent but not homeomorphic lens spaces may have configuration spaces with different homotopy types, which can be detected by different Massey product
Massey product
In algebraic topology, the Massey product is a cohomology operation of higher order introduced in , which generalizes the cup product.-Massey triple product:...
s.
External links
- Lens spaces at the Manifold Atlas.
- Lens spaces: a history at the Manifold Atlas.