PSL(2,7)
Encyclopedia
In mathematics
, the projective special linear group PSL(2,7) is a finite
simple group
that has important applications in algebra
, geometry
, and number theory
. It is the automorphism group of the Klein quartic
as well as the symmetry group
of the Fano plane
. With 168 elements PSL(2,7) is the second-smallest nonabelian
simple group
after the alternating group A5 on five letters with 60 elements (the rotational icosahedral symmetry
group), or the isomorphic PSL(2,5).
GL(2,7) consists of all invertible 2×2 matrices
over F7, the finite field
with 7 elements. These have nonzero determinant. The subgroup
SL(2,7) consists of all such matrices with unit determinant
. Then PSL(2,7) is defined to be the quotient group
obtained by identifying I and −I, where I is the identity matrix
. In this article, we let G denote any group isomorphic to PSL(2,7).
It is a general result that PSL(n, q) is simple
for n ≥ 2, q ≥ 2 (q being some power of a prime number), unless (n, q) = (2,2) or (2,3). PSL(2, 2) is isomorphic
to the symmetric group
S3, and PSL(2,3) is isomorphic to alternating group A4. In fact, PSL(2,7) is the second smallest nonabelian
simple group, after the alternating group A5 = PSL(2,5) = PSL(2,4).
P1(7) over the field with 7 elements:
Every orientation-preserving automorphism of P1(7) arises in this way, and so G = PSL(2,7) can be thought of geometrically as a group of symmetries of the projective line P1(7); the full group of possibly orientation-reversing projective linear automorphisms is instead the order 2 extension PGL(2,7), and the group of collineation
s of the projective line is the complete symmetric group
of the points.
However, PSL(2,7) is also isomorphic
to PSL(3,2) (= SL(3,2) = GL(3,2)), the special (general) linear group of 3×3 matrices over the field with 2 elements. In a similar fashion, G = PSL(3,2) acts on the projective plane
P2(2) over the field with 2 elements — also known as the
Fano plane
:
Again, every automorphism of P2(2) arises in this way, and so G = PSL(3,2) can be thought of geometrically as the symmetry group
of
this projective plane. The Fano plane
can be used to describe multiplication
of octonions, so G acts on the set of octonion multiplication tables.
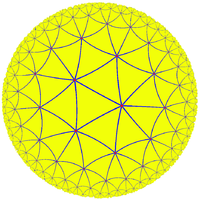The Klein quartic
is a Riemann surface
, the most symmetrical
curve of genus 3 over the complex number
s C.
Its group of conformal transformations is none other than G. No other
curve of genus 3 has as many conformal transformations. In fact, Adolf Hurwitz
proved that a curve of genus g has at most
(for g > 1); this is Hurwitz's automorphisms theorem.
As with all Hurwitz surface
s, the Klein quartic can be given a metric of constant negative curvature and then tiled with regular
heptagons, as a quotient of the order-3 heptagonal tiling, with the symmetries of the surface as a Riemannian surface or algebraic curve exactly the same as the symmetries of the tiling. For the Klein quartic this yields a tiling by 24 heptagons, and the order of G is thus related to the fact that
24 × 7 = 168.
Dually, it can be tiled with 56 equilateral triangles, with 24 vertices, each of degree 7, as a quotient of the order-7 triangular tiling. This tiling can be polyhedrally immersed in Euclidean 3-space as the small cubicuboctahedron
, which has 24 vertices.
Klein's quartic arises in many fields of mathematics, including representation theory, homology theory, octonion multiplication, Fermat's last theorem
, and Stark's theorem on imaginary quadratic number fields of class number 1.
M21; the Mathieu group M21 and then the Mathieu group M24 can be constructed as extensions of PSL(2,7). These extensions can be interpreted in term of the tiling of the Klein quartic, but are not realized by geometric symmetries of the tiling.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the projective special linear group PSL(2,7) is a finite
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
that has important applications in algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, and number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. It is the automorphism group of the Klein quartic
Klein quartic
In hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed...
as well as the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of the Fano plane
Fano plane
In finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
. With 168 elements PSL(2,7) is the second-smallest nonabelian
Nonabelian group
In mathematics, a non-abelian group, also sometimes called a non-commutative group, is a group in which there are at least two elements a and b of G such that a * b ≠ b * a...
simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
after the alternating group A5 on five letters with 60 elements (the rotational icosahedral symmetry
Icosahedral symmetry
A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
group), or the isomorphic PSL(2,5).
Definition
The general linear groupGeneral linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(2,7) consists of all invertible 2×2 matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
over F7, the finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with 7 elements. These have nonzero determinant. The subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
SL(2,7) consists of all such matrices with unit determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
. Then PSL(2,7) is defined to be the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
- SL(2,7) / {I,−I}
obtained by identifying I and −I, where I is the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. In this article, we let G denote any group isomorphic to PSL(2,7).
Properties
G = PSL(2,7) has 168 elements. This can be seen by counting the possible columns; there are 72 − 1 = 48 possibilities for the first column, then 72 − 7 = 42 possibilities for the second column. We must divide by 7 − 1 = 6 to force the determinant equal to one, and then we must divide by 2 when we identify I and −I. The result is (48×42) / (6×2) = 168.It is a general result that PSL(n, q) is simple
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
for n ≥ 2, q ≥ 2 (q being some power of a prime number), unless (n, q) = (2,2) or (2,3). PSL(2, 2) is isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
S3, and PSL(2,3) is isomorphic to alternating group A4. In fact, PSL(2,7) is the second smallest nonabelian
Nonabelian group
In mathematics, a non-abelian group, also sometimes called a non-commutative group, is a group in which there are at least two elements a and b of G such that a * b ≠ b * a...
simple group, after the alternating group A5 = PSL(2,5) = PSL(2,4).
Actions on projective spaces
G = PSL(2,7) acts via linear fractional transformation on the projective lineProjective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
P1(7) over the field with 7 elements:
Every orientation-preserving automorphism of P1(7) arises in this way, and so G = PSL(2,7) can be thought of geometrically as a group of symmetries of the projective line P1(7); the full group of possibly orientation-reversing projective linear automorphisms is instead the order 2 extension PGL(2,7), and the group of collineation
Collineation
In projective geometry, a collineation is a one-to-one and onto map from one projective space to another, or from a projective space to itself, such that the images of collinear points are themselves collinear. All projective linear transformations induce a collineation...
s of the projective line is the complete symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
of the points.
However, PSL(2,7) is also isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to PSL(3,2) (= SL(3,2) = GL(3,2)), the special (general) linear group of 3×3 matrices over the field with 2 elements. In a similar fashion, G = PSL(3,2) acts on the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
P2(2) over the field with 2 elements — also known as the
Fano plane
Fano plane
In finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
:
Again, every automorphism of P2(2) arises in this way, and so G = PSL(3,2) can be thought of geometrically as the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of
this projective plane. The Fano plane
Fano plane
In finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
can be used to describe multiplication
of octonions, so G acts on the set of octonion multiplication tables.
Symmetries of the Klein quartic
Klein quartic
In hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed...
- x3y + y3z + z3x = 0
is a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
, the most symmetrical
curve of genus 3 over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s C.
Its group of conformal transformations is none other than G. No other
curve of genus 3 has as many conformal transformations. In fact, Adolf Hurwitz
Adolf Hurwitz
Adolf Hurwitz was a German mathematician.-Early life:He was born to a Jewish family in Hildesheim, former Kingdom of Hannover, now Lower Saxony, Germany, and died in Zürich, in Switzerland. Family records indicate that he had siblings and cousins, but their names have yet to be confirmed...
proved that a curve of genus g has at most
- 84(g − 1) conformal transformations
(for g > 1); this is Hurwitz's automorphisms theorem.
Hurwitz surface
In Riemann surface theory and hyperbolic geometry, a Hurwitz surface, named after Adolf Hurwitz, is a compact Riemann surface with preciselyautomorphisms, where g is the genus of the surface. This number is maximal by virtue of Hurwitz's theorem on automorphisms...
s, the Klein quartic can be given a metric of constant negative curvature and then tiled with regular
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
heptagons, as a quotient of the order-3 heptagonal tiling, with the symmetries of the surface as a Riemannian surface or algebraic curve exactly the same as the symmetries of the tiling. For the Klein quartic this yields a tiling by 24 heptagons, and the order of G is thus related to the fact that
24 × 7 = 168.
Dually, it can be tiled with 56 equilateral triangles, with 24 vertices, each of degree 7, as a quotient of the order-7 triangular tiling. This tiling can be polyhedrally immersed in Euclidean 3-space as the small cubicuboctahedron
Small cubicuboctahedron
In geometry, the small cubicuboctahedron is a uniform star polyhedron, indexed as U13. It has 20 faces , 48 edges, and 24 vertices. Its vertex figure is a crossed quadrilateral.- Related polyhedra :...
, which has 24 vertices.
Klein's quartic arises in many fields of mathematics, including representation theory, homology theory, octonion multiplication, Fermat's last theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
, and Stark's theorem on imaginary quadratic number fields of class number 1.
Mathieu group
PSL(2,7) is a maximal subgroup of the Mathieu groupMathieu group
In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...
M21; the Mathieu group M21 and then the Mathieu group M24 can be constructed as extensions of PSL(2,7). These extensions can be interpreted in term of the tiling of the Klein quartic, but are not realized by geometric symmetries of the tiling.
Group actions
PSL(2,7) acts on various sets:- Interpreted as linear automorphisms of the projective line over
it acts 2-transitively on a set of 8 points, with stabilizer of order 3. (PGL(2,7) acts sharply 3-transitively, with trivial stabilizer.) - Interpreted as automorphisms of a tiling of the Klein quartic, it acts simply transitively on the 24 vertices (or dually, 24 heptagons), with stabilizer of order 7 (corresponding to rotation about the vertex/heptagon).
- Interpreted as a subgroup of the Mathieu group M21, which acts on 21 points, it does not act transitively on the 21 points.