Collineation
Encyclopedia
In projective geometry
, a collineation is a one-to-one and onto map (a bijection
) from one projective space
to another, or from a projective space to itself, such that the images of collinear points are themselves collinear. All projective linear transformations induce a collineation. A collineation of a projective space to itself is also called an automorphism
, and the set of all collineations of a space to itself form a group
, called the collineation group.
Formally, let V be a vector space over a field K and W a vector space over a field L. Consider the projective spaces PG(V) and PG(W).
Call D(V) and D(W) the set of subspaces of V and W respectively. A collineation from PG(V) to PG(W) is a map α : D(V) → D(W), such that:
(a set of points P, lines L, and an incidence relation I specifying which points lie on which lines, satisfying certain axioms), a collineation between projective spaces thus defined then being a bijective function f between the sets of points and a bijective function g between the set of lines, preserving the incidence relation."Preserving the incidence relation" means that if point p is on line l then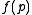
is in 
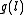; formally, if 
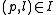then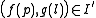 
.
Every projective space of dimension greater than or equal to three is isomorphic to the projectivization of a linear space over a division ring
, so in these dimensions this definition is no more general than the linear-algebraic one above, but in dimension two there are other projective planes, namely the non-Desarguesian plane
s, and this definition allows one to define a map of such projective planes.
For dimension one, any set of points lying on a single projective line defines a projective space, though the resulting notion of collineation is just any bijection of the set.
of the points of the projective line. This is different from the behavior in higher dimensions, and thus alternatively, one can give a more restrictive definition, so that the fundamental theorem of projective geometry holds.
In this definition, when V has dimension two, a collineation from PG(V) to PG(W) is a map α : D(V) → D(W), such that :
This last requirement ensures that collineations are all semilinear maps.
) and automorphic collineations. For projective spaces coming from a linear space, the fundamental theorem of projective geometry states that all collineations are a combination of these, as described below.
A duality
is a collineation from a projective space onto its dual space, taking points to hyperplanes (and vice versa) and preserving incidence. A correlation
is a duality from a projective space onto itself (this implies that the space is self-dual). A polarity is an involutory correlation.
of homographies by automorphic collineations – assuming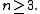
In particular, the collineations of PG(2, R) are exactly the homographies, as Gal(R/Q) is trivial.
Suppose φ is a semilinear nonsingular map from V to W, with the dimension of V at least three. Define α : D(V) → D(W) by saying that Zα = { φ(z) | z ∈ Z } for all Z in D(V). As φ is semilinear, one easily checks that this map is properly defined, and further more, as φ is not singular, it is bijective. It is obvious now that α is a collineation. We say α is induced by φ.
The fundamental theorem of projective geometry states the converse:
Suppose V is a vector space over a field K with dimension at least three, W is a vector space over a field L, and α is a collineation from PG(V) to PG(W). This implies K and L are isomorphic fields, V and W have the same dimension, and there is a semilinear map φ such that φ induces α.
For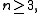
the collineation group is the projective semilinear group, 
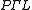– this is PGL, twisted by field automorphisms; formally, the semidirect product
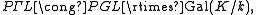where k is the prime field for K.
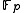or 
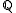), we have 
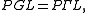but for K not a prime field (such as 
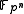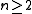for 
or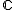 
), the projective linear group is in general a proper subgroup of the collineation group, which can be thought of as "transformations preserving a projective semi-linear structure". Correspondingly, the quotient group 
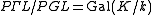corresponds to "choices of linear structure", with the identity (base point) being the existing linear structure. Given a projective space without an identification as the projectivization of a linear space, there is no natural isomorphism between the collineation group and PΓL, and the choice of a linear structure (realization as projectivization of a linear space) corresponds to a choice of subgroup 
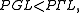these choices forming a torsor over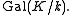 
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, a collineation is a one-to-one and onto map (a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
) from one projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
to another, or from a projective space to itself, such that the images of collinear points are themselves collinear. All projective linear transformations induce a collineation. A collineation of a projective space to itself is also called an automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
, and the set of all collineations of a space to itself form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, called the collineation group.
Definition
Simply, a collineation is a one-to-one map from one projective space to another, or from a projective space to itself, such that the images of collinear points are themselves collinear. One may formalize this using various ways of presenting a projective space. Also, the case of the projective line is special, and hence generally treated differently.Linear algebra
For a projective space defined in terms of linear algebra (as the projectivization of a vector space), a collineation is a map between the projective spaces that is order-preserving with respect to inclusion of subspaces; this is also referred to as a projectivity.Formally, let V be a vector space over a field K and W a vector space over a field L. Consider the projective spaces PG(V) and PG(W).
Call D(V) and D(W) the set of subspaces of V and W respectively. A collineation from PG(V) to PG(W) is a map α : D(V) → D(W), such that:
- α is a bijection.
- A ⊆ B ↔ Aα ⊆ Bα for all A, B in D(V).
Axiomatically
Given a projective space defined axiomatically in terms of an incidence structureIncidence structure
In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
(a set of points P, lines L, and an incidence relation I specifying which points lie on which lines, satisfying certain axioms), a collineation between projective spaces thus defined then being a bijective function f between the sets of points and a bijective function g between the set of lines, preserving the incidence relation."Preserving the incidence relation" means that if point p is on line l then
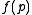is in 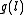; formally, if 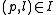then 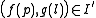.Every projective space of dimension greater than or equal to three is isomorphic to the projectivization of a linear space over a division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
, so in these dimensions this definition is no more general than the linear-algebraic one above, but in dimension two there are other projective planes, namely the non-Desarguesian plane
Non-Desarguesian plane
In mathematics, a non-Desarguesian plane, named after Gérard Desargues, is a projective plane that does not satisfy Desargues's theorem, or in other words a plane that is not a Desarguesian plane...
s, and this definition allows one to define a map of such projective planes.
For dimension one, any set of points lying on a single projective line defines a projective space, though the resulting notion of collineation is just any bijection of the set.
Collineations of the projective line
For a projective space of dimension one (a projective line; the projectivization of a vector space of dimension two), all points are collinear, so the collineation group is exactly the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
of the points of the projective line. This is different from the behavior in higher dimensions, and thus alternatively, one can give a more restrictive definition, so that the fundamental theorem of projective geometry holds.
In this definition, when V has dimension two, a collineation from PG(V) to PG(W) is a map α : D(V) → D(W), such that :
- 0 is mapped onto the trivial subspace of W.
- V is mapped onto W.
- There is a nonsingular semilinear mapSemilinear transformationIn linear algebra, particularly projective geometry, a semilinear transformation between vector spaces V and W over a field K is a function that is a linear transformation "up to a twist", hence semi-linear, where "twist" means "field automorphism of K"...
β from V to W such that, for all v in V,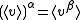
This last requirement ensures that collineations are all semilinear maps.
Types
The main examples of collineations are projective linear transformations (also known as homographiesHomography
Homography is a concept in the mathematical science of geometry.A homography is an invertible transformation from a projective space to itself that maps straight lines to straight lines...
) and automorphic collineations. For projective spaces coming from a linear space, the fundamental theorem of projective geometry states that all collineations are a combination of these, as described below.
A duality
Duality (projective geometry)
A striking feature of projective planes is the "symmetry" of the roles played by points and lines in the definitions and theorems, and duality is the formalization of this metamathematical concept. There are two approaches to the subject of duality, one through language and the other a more...
is a collineation from a projective space onto its dual space, taking points to hyperplanes (and vice versa) and preserving incidence. A correlation
Correlation (projective geometry)
A correlation is a duality from a projective space to itself...
is a duality from a projective space onto itself (this implies that the space is self-dual). A polarity is an involutory correlation.
Projective linear transformations
Projective linear transformations (homographies) are collineations (planes in a vector space correspond to lines in the associated projective space, and linear transformations map planes to planes, so projective linear transformations map lines to lines), but in general not all collineations are projective linear transformations – PGL is in general a proper subgroup of the collineation group.Automorphic collineations
An is a map that, in coordinates, is a field automorphism applied to the coordinates.Fundamental theorem of projective geometry
Briefly, every collineation is the product of a homography (a projective linear transformation) and an automorphic collineation. More precisely, the collineation group is the projective semilinear group, which is the semidirect productSemidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of homographies by automorphic collineations – assuming
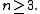
In particular, the collineations of PG(2, R) are exactly the homographies, as Gal(R/Q) is trivial.
Suppose φ is a semilinear nonsingular map from V to W, with the dimension of V at least three. Define α : D(V) → D(W) by saying that Zα = { φ(z) | z ∈ Z } for all Z in D(V). As φ is semilinear, one easily checks that this map is properly defined, and further more, as φ is not singular, it is bijective. It is obvious now that α is a collineation. We say α is induced by φ.
The fundamental theorem of projective geometry states the converse:
Suppose V is a vector space over a field K with dimension at least three, W is a vector space over a field L, and α is a collineation from PG(V) to PG(W). This implies K and L are isomorphic fields, V and W have the same dimension, and there is a semilinear map φ such that φ induces α.
For
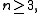the collineation group is the projective semilinear group, 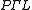– this is PGL, twisted by field automorphisms; formally, the semidirect productSemidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
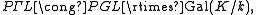where k is the prime field for K.Linear structure
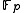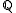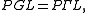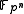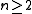Thus for K a prime field ( or ), we have but for K not a prime field (such as for or 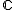), the projective linear group is in general a proper subgroup of the collineation group, which can be thought of as "transformations preserving a projective semi-linear structure". Correspondingly, the quotient group 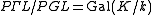corresponds to "choices of linear structure", with the identity (base point) being the existing linear structure. Given a projective space without an identification as the projectivization of a linear space, there is no natural isomorphism between the collineation group and PΓL, and the choice of a linear structure (realization as projectivization of a linear space) corresponds to a choice of subgroup 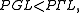these choices forming a torsor over