In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the Bolza surface, alternatively, complex algebraic Bolza curve (named after Oskar Bolza

Oskar Bolza

Oskar Bolza was a German mathematician, and student of Felix Klein. He was born in Bad Bergzabern, Rhenish Palatinate, and his parents were Luise Koenig and Moritz Bolza....

), is a compact Riemann surface

Riemann surface

In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...

 of genus

Genus (mathematics)

In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...

 2 with the highest possible order of the conformal automorphism group

Conformal map

In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...

 in this genus, namely 48. An affine model for the Bolza surface can be obtained as the locus of the equation


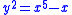
in . Of all genus 2 hyperbolic surfaces, the Bolza surface has the highest systole. As a hyperelliptic surface, it arises as the ramified double cover of the 2-sphere, with ramification locus at the six vertices of a regular octahedron

Octahedral symmetry

150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...

 inscribed in the sphere, as can be readily seen from the equation above.

Triangle surface

The Bolza surface is a (2,3,8) triangle surface – see Schwarz triangle

Schwarz triangle

In geometry, a Schwarz triangle, named after Hermann Schwarz is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in ....

. More specifically, the Fuchsian group defining the Bolza surface is a subgroup of the group generated by reflections in the sides of a hyperbolic triangle with angles . More specifically, it is a subgroup of the index

Index of a subgroup

In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...

-two subgroup of the group of reflections, which consists of products of an even number of reflections, which has an abstract presentation in terms of generators 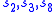and relations as well as . The Fuchsian group defining the Bolza surface is also a subgroup of the (3,3,4) triangle group

Triangle group

In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...

, which is a subgroup of index 2 in the (2,3,8) triangle group. It is interesting to note that the (2,3,8) group does not have a realisation in terms of a quaternion algebra, but the (3,3,4) group does.

Quaternion algebra

Following MacLachlan and Reid, the quaternion algebra

Quaternion algebra

In mathematics, a quaternion algebra over a field F is a central simple algebra A over F that has dimension 4 over F. Every quaternion algebra becomes the matrix algebra by extending scalars , i.e...

 can be taken to be the algebra over generated as an associative algebra by generators i,j and relations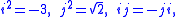

with an appropriate choice of an order.