.gif)
Regular map (graph theory)
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a regular map is a symmetric tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
of a closed surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
. More precisely, a regular map is a decomposition of a two-dimensional manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
such as a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, or Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
into topological disks, such that every flag (an incident vertex-edge-face triple) can be transformed into any other flag by a symmetry of the decomposition. Regular maps are, in a sense, topological generalizations of Platonic solids. The theory of maps and their classification is related to the theory of Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s, hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, and Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
. Regular maps are classified according to either: the genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
and orientability
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
of the supporting surface, the underlying graph
Graph embedding
In topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...
, or the automorphism group.
Overview
Regular maps are typically defined and studied in three ways: topologically, group-theoretically, and graph-theoretically.Topological approach
Topologically, a map is a 2-cellCW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
decomposition of a closed compact 2-manifold.
The genus g, of a map M is given by Euler's relation
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
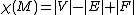 which is equal to
which is equal to 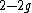 if the map is orientable, and
if the map is orientable, and 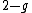 if the map is non-orientable. It is a crucial fact that there is a finite (non-zero) number of regular maps for every orientable genus except the torus.
if the map is non-orientable. It is a crucial fact that there is a finite (non-zero) number of regular maps for every orientable genus except the torus.Group-theoretical approach
Group-theoretically, the permutation representation of a regular map M is a transitive permutation groupPermutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
C, on a set
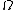 of flags, generated by a fixed-point free involutions r0, r1, r2 satisfying (r0r2)2= I. In this definition the faces are the orbit of F = <r0, r1>, edges are the orbit of E = <r0, r2>, and vertices are the orbit of V = <r1, r2>. More abstractly, the automorphism group of any regular map is the non-degenerate, homomorphic image of a <2,m,n>-triangle group
of flags, generated by a fixed-point free involutions r0, r1, r2 satisfying (r0r2)2= I. In this definition the faces are the orbit of F = <r0, r1>, edges are the orbit of E = <r0, r2>, and vertices are the orbit of V = <r1, r2>. More abstractly, the automorphism group of any regular map is the non-degenerate, homomorphic image of a <2,m,n>-triangle groupTriangle group
In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...
.
Graph-theoretical approach
Graph-theoretically, a map is a cubic graph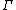 with edges coloured blue, yellow, red such that:
with edges coloured blue, yellow, red such that: 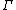 is connected, every vertex is incident to one edge of each colour, and cycles of edges not coloured blue, have length 4. Note that
is connected, every vertex is incident to one edge of each colour, and cycles of edges not coloured blue, have length 4. Note that 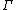 is the flag graph or graph encoded map (GEM) of the map, defined on the vertex set of flags
is the flag graph or graph encoded map (GEM) of the map, defined on the vertex set of flags 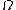 and is not the skeleton G = (V,E) of the map. In general, |
and is not the skeleton G = (V,E) of the map. In general, |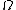 | = 4|E|.
| = 4|E|.A map M is regular iff Aut(M) acts
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
regularly on the flags. Aut(M) of a regular map is transitive on the vertices, edges, and faces of M. A map M is said to be reflexible iff Aut(M) is regular and contains an automorphism
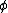 that fixes both a vertex v and a face f, but reverses the order of the edges. A map which is regular but not reflexible is said to be chiral
that fixes both a vertex v and a face f, but reverses the order of the edges. A map which is regular but not reflexible is said to be chiralChirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
.
Examples
- The Great dodecahedron is a regular map with pentagonal faces on the orientable surface of genus 4.
- The hemicube is a regular map of type {4,3}

- The hemi-dodecahedronHemi-dodecahedronA hemi-dodecahedron is an abstract regular polyhedron, containing half the faces of a regular dodecahedron. It can be realized as a projective polyhedron , which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and...
is a regular map produced by pentagonal embedding of the Petersen graph in the projective plane. - The p-Hosohedron is a regular map of type {2, p}. Note that the hosohedron is non-polyhedral in the sense that it is not an abstract polytopeAbstract polytopeIn mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...
. In particular, it doesn't satisfy the diamond property. - The Dyck map is a regular map of 12 octagons on a genus-3 surface. Its underlying graph, the Dyck graphDyck graphIn the mathematical field of graph theory, the Dyck graph is a 3-regular graph with 32 vertices and 48 edges, named after Walther von Dyck.It is Hamiltonian with 120 distinct Hamiltonian cycles. It has chromatic number 2, chromatic index 3, radius 5, diameter 5 and girth 6...
, can also form a regular map of 16 hexagons on a torus.
The following is the complete determination of simple reflexible maps of positive Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
: the sphere and the projective plane (Coxeter 80).
| Characteristic | Genus | Schläfli symbol | Group | Graph | Notes |
| 2 | 0 | {p,2} | C2 × Dihp | Cp Cycle graph In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn... |
Dihedron |
| 2 | 0 | {2,p} | C2 × Dihp | p-fold K2 Complete graph In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:... |
Hosohedron |
| 2 | 0 | {3,3} | Sym4 | K4 Complete graph In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:... |
Tetrahedron |
| 2 | 0 | {4,3} | C2 × Sym4 | K2,2,2 | Octahedron |
| 2 | 0 | {3,4} | C2 × Sym4 | K4 Complete graph In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:... × Tensor product of graphs In graph theory, the tensor product G × H of graphs G and H is a graph such that* the vertex set of G × H is the Cartesian product V × V; and... K2 Complete graph In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:... |
Cube |
| 2 | 0 | {5,3} | C2 × Alt5 | Dodecahedron | |
| 2 | 0 | {3,5} | C2 × Alt5 | K6 Complete graph In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:... × Tensor product of graphs In graph theory, the tensor product G × H of graphs G and H is a graph such that* the vertex set of G × H is the Cartesian product V × V; and... K2 Complete graph In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:... |
Icosahedron |
| 1 | - | {2p,2}/2 | Dih2p | Cp Cycle graph In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn... |
Hemidihedron |
| 1 | - | {2,2p}/2 | Dih2p | p-fold K2 Complete graph In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:... |
Hemihosohedron |
| 1 | - | {4,3} | Sym4 | K4 Complete graph In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:... |
Hemicube |
| 1 | - | {4,3} | Sym4 | 2-fold K3 Complete graph In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:... |
Hemioctahedron |
| 1 | - | {5,3} | Alt5 | Petersen graph Petersen graph In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it... |
Hemidodecahedron |
| 1 | - | {3,5} | Alt5 | K6 Complete graph In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:... |
Hemi-icosahedron |
See also
- Topological graph theoryTopological graph theoryIn mathematics topological graph theory is a branch of graph theory. It studies the embedding of graphs in surfaces, spatial embeddings of graphs, and graphs as topological spaces. It also studies immersions of graphs....
- Abstract polytopeAbstract polytopeIn mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...
- Planar graphPlanar graphIn graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
- Toroidal graphToroidal graphIn mathematics, a graph G is toroidal if it can be embedded on the torus. In other words, the graph's vertices can be placed on a torus such that no edges cross...
- Graph embeddingGraph embeddingIn topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...
- Regular tiling
- Platonic solidPlatonic solidIn geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...

