Planar graph - AbsoluteAstronomy.com

Example graphs
Planar	Nonplanar
Butterfly graph Butterfly graph In the mathematical field of graph theory, the butterfly graph is a planar undirected graph with 5 vertices and 6 edges...	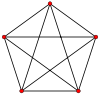K₅
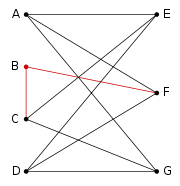
The complete graph Complete graph In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:... K₄ is planar	K_3,3

In graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, a planar graph is a graph

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

that can be embedded

Graph embedding

In topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...

in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other.

A planar graph already drawn in the plane without edge intersections is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point in 2D space, and from every edge to a plane curve

Plane curve

In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....

, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points. Plane graphs can be encoded by combinatorial maps.

It is easily seen that a graph that can be drawn on the plane can be drawn on the sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

as well, and vice versa.

The equivalence class of topologically equivalent drawings on the sphere is called a planar map. Although a plane graph has an external or unbounded face, none of the faces of a planar map have a particular status.

A generalization of planar graphs are graphs which can be drawn on a surface of a given genus

Genus (mathematics)

In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...

. In this terminology, planar graphs have graph genus 0, since the plane (and the sphere) are surfaces of genus 0. See "graph embedding

Graph embedding

" for other related topics.

Kuratowski's and Wagner's theorems

The Polish

Poland

Poland , officially the Republic of Poland , is a country in Central Europe bordered by Germany to the west; the Czech Republic and Slovakia to the south; Ukraine, Belarus and Lithuania to the east; and the Baltic Sea and Kaliningrad Oblast, a Russian exclave, to the north...

mathematician Kazimierz Kuratowski

Kazimierz Kuratowski

Kazimierz Kuratowski was a Polish mathematician and logician. He was one of the leading representatives of the Warsaw School of Mathematics.-Biography and studies:...

provided a characterization of planar graphs in terms of forbidden graphs, now known as Kuratowski's theorem:

A finite graph is planar if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

it does not contain a subgraph that is a subdivision of K₅ (the complete graph

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

on five vertices

Vertex (graph theory)

In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...

) or K_3,3 (complete bipartite graph

Complete bipartite graph

In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...

on six vertices, three of which connect to each of the other three).

A subdivision of a graph results from inserting vertices into edges (for example, changing an edge •——• to •—•—•) zero or more times. Equivalent formulations of this theorem, also known as "Theorem P" include

A finite graph is planar if and only if it does not contain a subgraph that is homeomorphic

Homeomorphism (graph theory)

In graph theory, two graphs G and G' are homeomorphic if there is an isomorphism from some subdivision of G to some subdivision of G'...

to K₅ or K_3,3.

In the Soviet Union

Soviet Union

The Soviet Union , officially the Union of Soviet Socialist Republics , was a constitutionally socialist state that existed in Eurasia between 1922 and 1991....

, Kuratowski's theorem was known as the Pontryagin-Kuratowski theorem, as its proof was allegedly first given in Pontryagin's unpublished notes. By a long-standing academic tradition, such references are not taken into account in determining priority, so the Russian name of the theorem is not acknowledged internationally.

Instead of considering subdivisions, Wagner's theorem deals with minors

Minor (graph theory)

In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....

A finite graph is planar if and only if it does not have K₅ or K_3,3 as a minor

Minor (graph theory)

In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....

Klaus Wagner

Klaus Wagner (mathematician)

Klaus Wagner was a German mathematician. He studied topology at the University of Cologne under the supervision of Karl Dörge, who had been a student of Issai Schur. Wagner received his Ph.D. in 1937, and taught at Cologne for many years himself...

asked more generally whether any minor-closed class of graphs is determined by a finite set of "forbidden minors". This is now the Robertson-Seymour theorem, proved in a long series of papers. In the language of this theorem, K₅ and K_3,3 are the forbidden minors for the class of finite planar graphs.

Other planarity criteria

In practice, it is difficult to use Kuratowski's criterion to quickly decide whether a given graph is planar. However, there exist fast algorithm

Algorithm

In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...

s for this problem: for a graph with n vertices, it is possible to determine in time O

Big O notation

In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...

(n) (linear time) whether the graph may be planar or not (see planarity testing

Planarity testing

In graph theory, the planarity testing problem asks whether, given a graph, that graph is a planar graph . This is a well-studied problem in computer science for which many practical algorithms have emerged, many taking advantage of novel data structures...

).

For a simple, connected, planar graph with v vertices and e edges, the following simple planarity criteria hold:

Theorem 1. If v ≥ 3 then e ≤ 3v − 6;

Theorem 2. If v > 3 and there are no cycles of length 3, then e ≤ 2v − 4.

In this sense, planar graphs are sparse graphs, in that they have only O(v) edges, asymptotically smaller than the maximum O(v²). The graph K_3,3, for example, has 6 vertices, 9 edges, and no cycles of length 3. Therefore, by Theorem 2, it cannot be planar. Note that these theorems provide necessary conditions for planarity that are not sufficient conditions, and therefore can only be used to prove a graph is not planar, not that it is planar. If both theorem 1 and 2 fail, other methods may be used.

For two planar graphs with v vertices, it is possible to determine in time O(v) whether they are isomorphic

Graph theory

or not (see also graph isomorphism problem

Graph isomorphism problem

The graph isomorphism problem is the computational problem of determining whether two finite graphs are isomorphic.Besides its practical importance, the graph isomorphism problem is a curiosity in computational complexity theory as it is one of a very small number of problems belonging to NP...

Whitney's planarity criterion gives a characterization based on the existence of an algebraic dual;
MacLane's planarity criterion gives an algebraic characterization of finite planar graphs, via their cycle space
Cycle space
In graph theory, an area of mathematics, a cycle space is a vector space defined from an undirected graph; elements of the cycle space represent formal combinations of cycles in the graph....

s;
Fraysseix–Rosenstiehl's planarity criterion gives a characterization based on the existence of a bipartition of the cotree edges of a depth-first search tree. It is central to the left-right planarity testing algorithm;
Schnyder's theorem
Schnyder's theorem
In graph theory, Schnyder's theorem is a characterization of planar graphs in termsof the order dimension of their incidence posets. It is named after Walter Schnyder, who published its proof in 1989....

gives a characterization of planarity in terms of partial order dimension
Order dimension
In mathematics, the dimension of a partially ordered set is the smallest number of total orders the intersection of which gives rise to the partial order....

;
Colin de Verdière's planarity criterion
Colin de Verdière graph invariant
Colin de Verdière's invariant is a graph parameter \mu for any graph G introduced by Yves Colin de Verdière in 1990. It was motivated by the study of the maximum multiplicity of the second eigenvalue of certain Schrödinger operators.-Definition:...

gives a characterization based on the maximum multiplicity of the second eigenvalue of certain Schrödinger operators defined by the graph.

Euler's formula

Euler's formula states that if a finite, connected

Connectivity (graph theory)

In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...

, planar graph is drawn in the plane without any edge intersections, and v is the number of vertices, e is the number of edges and f is the number of faces (regions bounded by edges, including the outer, infinitely-large region), then

v − e + f = 2.

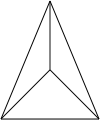
As an illustration, in the butterfly graph given above, v = 5, e = 6 and f = 3. If the second graph is redrawn without edge intersections, it has v = 4, e = 6 and f = 4.
In general, if the property holds for all planar graphs of f faces, any change to the graph that creates an additional face while keeping the graph planar would keep v − e + f an invariant. Since the property holds for all graphs with f = 2, by mathematical induction

Mathematical induction

Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...

it holds for all cases. Euler's formula can also be proven as follows: if the graph isn't a tree

Tree (graph theory)

In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...

, then remove an edge which completes a cycle

Cycle (graph theory)

In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...

. This lowers both e and f by one, leaving v − e + f constant. Repeat until the remaining graph is a tree; trees have v = e + 1 and f = 1, yielding v − e + f = 2. i.e. the Euler characteristic

Euler characteristic

In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...

is 2.

In a finite, connected

Connectivity (graph theory)

, simple, planar graph, any face (except possibly the outer one) is bounded by at least three edges and every edge touches at most two faces; using Euler's formula, one can then show that these graphs are sparse in the sense that e ≤ 3v − 6 if v ≥ 3.
A simple graph is called maximal planar if it is planar but adding any edge (on the given vertex set) would destroy that property. All faces (even the outer one) are then bounded by three edges, explaining the alternative terms triangular and triangulated for these graphs. If a triangular graph has v vertices with v > 2, then it has precisely 3v − 6 edges and 2v − 4 faces.

Euler's formula is also valid for simple polyhedra

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

. This is no coincidence: every simple polyhedron can be turned into a connected, simple, planar graph by using the polyhedron's vertices as vertices of the graph and the polyhedron's edges as edges of the graph. The faces of the resulting planar graph then correspond to the faces of the polyhedron. For example, the second planar graph shown above corresponds to a tetrahedron

Tetrahedron

In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...

. Not every connected, simple, planar graph belongs to a simple polyhedron in this fashion: the trees do not, for example. Steinitz's theorem

Steinitz's theorem

In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...

says that the polyhedral graph

Polyhedral graph

s formed from convex

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

polyhedra (equivalently: those formed from simple polyhedra) are precisely the finite 3-connected

Connectivity (graph theory)

simple planar graphs.

Kissing graphs

We say that two circles drawn in a plane kiss whenever they intersect at one point, and their interior does not overlap. Given a set of circles in the plane, we can draw its kissing graph by each circle as a vertex, and connect two vertices whenever their circles kiss. Koebe's

Paul Koebe

Paul Koebe was a 20th-century German mathematician. His work dealt exclusively with the complex numbers, his most important results being on the uniformization of Riemann surfaces in a series of four papers in 1907–1909. He did his thesis at Berlin, where he worked under Herman Schwarz...

theorem states that

Koebe's theorem (1936): A graph is planar if and only if it is a kissing graph of circles.

The theorem is an improvement over Wagner's theorem, which says that

Wagner's theorem (1936): A planar graph has a plane embedding using only straight lines as edges.

Related families of graphs

Outerplanar graph

In graph theory, an undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges...

s are graphs with an embedding in the plane such that all vertices belong to the unbounded face of the embedding. Every outerplanar graph is planar, but the converse is not true: K₄ is planar but not outerplanar. A theorem similar to Kuratowski's states that a finite graph is outerplanar if and only if it does not contain a subdivision of K₄ or of K_2,3.

A 1-outerplanar embedding of a graph is the same as an outerplanar embedding. For k > 1 a planar embedding is k-outerplanar if removing the vertices on the outer face results in a (k − 1)-outerplanar embedding. A graph is k-outerplanar if it has a k-outerplanar embedding

An apex graph

Apex graph

In graph theory, a branch of mathematics, an apex graph is a graph that can be made planar by the removal of a single vertex. The deleted vertex is called an apex of the graph. We say an apex, not the apex because an apex graph may have more than one apex...

is a graph that may be made planar by the removal of one vertex, and a k-apex graph is a graph that may be made planar by the removal of at most k vertices.

A toroidal graph

Toroidal graph

In mathematics, a graph G is toroidal if it can be embedded on the torus. In other words, the graph's vertices can be placed on a torus such that no edges cross...

is a graph that can be embedded without crossings on the torus

Torus

In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...

. More generally, the genus

Genus (mathematics)

of a graph is the minimum genus of a two-dimensional graph onto which the graph may be embedded; planar graphs have genus zero and nonplanar toroidal graphs have genus one.

Any graph may be embedded into three-dimensional space without crossings. However, a three-dimensional analogue of the planar graphs is provided by the linklessly embeddable graphs

Linkless embedding

In topological graph theory, a mathematical discipline, a linkless embedding of an undirected graph is an embedding of the graph into Euclidean space in such a way that no two cycles of the graph have nonzero linking number. A flat embedding is an embedding with the property that every cycle is the...

, graphs that can be embedded into three-dimensional space in such a way that no two cycles are topologically linked

Linking number

In mathematics, the linking number is a numerical invariant that describes the linking of two closed curves in three-dimensional space. Intuitively, the linking number represents the number of times that each curve winds around the other...

with each other. In analogy to Kuratowski's and Wagner's characterizations of the planar graphs as being the graphs that do not contain K₅ or K_3,3 as a minor, the linklessly embeddable graphs may be characterized as the graphs that do not contain as a minor any of the seven graphs in the Petersen family

Petersen family

In graph theory, the Petersen family is a set of seven undirected graphs that includes the Petersen graph and the complete graph K6. The Petersen family is named after Danish mathematician Julius Petersen, the namesake of the Petersen graph....

. In analogy to the characterizations of the outerplanar and planar graphs as being the graphs with Colin de Verdière graph invariant

Colin de Verdière graph invariant

Colin de Verdière's invariant is a graph parameter \mu for any graph G introduced by Yves Colin de Verdière in 1990. It was motivated by the study of the maximum multiplicity of the second eigenvalue of certain Schrödinger operators.-Definition:...

at most two or three, the linklessly embeddable graphs are the graphs that have Colin de Verdière invariant at most four.

Other facts and definitions

Every planar graph without loops is 4-partite, or 4-colorable

Graph coloring

In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...

; this is the graph-theoretical formulation of the four color theorem

Four color theorem

In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...

.

Fáry's theorem

Fáry's theorem

In mathematics, Fáry's theorem states that any simple planar graph can be drawn without crossings so that its edges are straight line segments. That is, the ability to draw graph edges as curves instead of as straight line segments does not allow a larger class of graphs to be drawn...

states that every simple planar graph admits an embedding in the plane such that all edges are straight line segments which don't intersect. Similarly, every simple outerplanar graph admits an embedding in the plane such that all vertices lie on a fixed circle and all edges are straight line segments that lie inside the disk and don't intersect.

Given an embedding G of a (not necessarily simple) connected graph in the plane without edge intersections, we construct the dual graph
Dual graph
In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...

G* as follows: we choose one vertex in each face of G (including the outer face) and for each edge e in G we introduce a new edge in G* connecting the two vertices in G* corresponding to the two faces in G that meet at e. Furthermore, this edge is drawn so that it crosses e exactly once and that no other edge of G or G* is intersected. Then G* is again the embedding of a (not necessarily simple) planar graph; it has as many edges as G, as many vertices as G has faces and as many faces as G has vertices. The term "dual" is justified by the fact that G** = G; here the equality is the equivalence of embeddings on the sphere

Sphere

. If G is the planar graph corresponding to a convex polyhedron, then G* is the planar graph corresponding to the dual polyhedron.

Duals are useful because many properties of the dual graph are related in simple ways to properties of the original graph, enabling results to be proven about graphs by examining their dual graphs.

While the dual constructed for a particular embedding is unique (up to isomorphism

Isomorphism

In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...

), graphs may have different (i.e. non-isomorphic) duals, obtained from different (i.e. non-homeomorphic) embeddings.

A Euclidean graph is a graph in which the vertices represent points in the plane, and the edges are assigned lengths equal to the Euclidean distance between those points; see Geometric graph theory

Geometric graph theory

In mathematics, a geometric graph is a graph in which the vertices or edges are associated with geometric objects or configurations. Geometric graph theory is a specialization of graph theory that studies geometric graphs...

.

A plane graph is said to be convex if all of its faces (including the outer face) are convex polygon

Convex polygon

In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...

s. A planar graph may be drawn convexly if and only if it is a subdivision of a 3-vertex-connected

K-vertex-connected graph

In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...

planar graph.

The circle packing theorem

Circle packing theorem

The circle packing theorem describes the possible tangency relations between circles in the plane whose interiors are disjoint. A circle packing is a connected collection of circles whose interiors are disjoint...

states that the family of planar graphs coincides with the family of intersection graph

Intersection graph

In the mathematical area of graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph may be represented as an intersection graph, but some important special classes of graphs may be defined by the types of sets that are used to form...

s for the sets of closed disks in the plane which intersect only at boundary points. Similarly, Scheinerman's conjecture

Scheinerman's conjecture

In mathematics, Scheinerman's conjecture, now a theorem, states that every planar graph is the intersection graph of a set of line segments in the plane. This conjecture was formulated by E. R. Scheinerman in his Ph.D. thesis , following earlier results that every planar graph could be represented...

(now a theorem) states that every planar graph can also be represented as an intersection graph of line segment

Line segment

In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...

s in the plane.

The planar separator theorem

Planar separator theorem

In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices...

states that every n-vertex planar graph can be partitioned into two subgraphs of size at most 2n/3 by the removal of O(√n) vertices. As a consequence, planar graphs also have treewidth and branch-width O(√n).

Applications

Telecommunications – e.g. spanning tree
Spanning tree
Spanning tree can refer to:* Spanning tree , a tree which contains every vertex of a more general graph* Spanning tree protocol, a protocol for finding spanning trees in bridged networks...

s
Vehicle routing – e.g. planning routes on road
Road
A road is a thoroughfare, route, or way on land between two places, which typically has been paved or otherwise improved to allow travel by some conveyance, including a horse, cart, or motor vehicle. Roads consist of one, or sometimes two, roadways each with one or more lanes and also any...

s without underpasses
VLSI – e.g. laying out circuit
Integrated circuit
An integrated circuit or monolithic integrated circuit is an electronic circuit manufactured by the patterned diffusion of trace elements into the surface of a thin substrate of semiconductor material...

s on computer chips
The puzzle game Planarity
Planarity
Planarity is a puzzle computer game based on a concept by Mary Radcliffe at Western Michigan University. The name comes from the term planar graph. In graph theory, a planar graph is a graph that can be embedded in a plane so that no edges intersect...

requires the player to "untangle" a planar graph so that none of its edges intersect.

External links

Edge Addition Planarity Algorithm Source Code, version 1.0 — Free C source code for reference implementation of Boyer-Myrvold planarity algorithm, which provides both a combinatorial planar embedder and Kuratowski subgraph isolator. An open source project with free licensing provides the Edge Addition Planarity Algorithms, current version.
Public Implementation of a Graph Algorithm Library and Editor — GPL graph algorithm library including planarity testing, planarity embedder and Kuratowski subgraph exhibition in linear time.
Boost Graph Library tools for planar graphs, including linear time planarity testing, embedding, Kuratowski subgraph isolation, and straight-line drawing.
3 Utilities Puzzle and Planar Graphs
Planarity — A puzzle game created by John Tantalo.
NetLogo Planarity model — NetLogo version of John Tantalo's game

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.