Graph coloring - AbsoluteAstronomy.com

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, graph coloring is a special case of graph labeling

Graph labeling

In the mathematical discipline of graph theory, a graph labeling is the assignment of labels, traditionally represented by integers, to the edges or vertices, or both, of a graph....

; it is an assignment of labels traditionally called "colors" to elements of a graph

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices

Vertex (graph theory)

In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...

share the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges share the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

Vertex coloring is the starting point of the subject, and other coloring problems can be transformed into a vertex version. For example, an edge coloring of a graph is just a vertex coloring of its line graph

Line graph

In graph theory, the line graph L of undirected graph G is another graph L that represents the adjacencies between edges of G...

, and a face coloring of a planar graph

Planar graph

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...

is just a vertex coloring of its planar dual

Dual graph

In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...

. However, non-vertex coloring problems are often stated and studied as is. That is partly for perspective, and partly because some problems are best studied in non-vertex form, as for instance is edge coloring.

The convention of using colors originates from coloring the countries of a map, where each face is literally colored. This was generalized to coloring the faces of a graph embedded

Graph embedding

In topological graph theory, an embedding of a graph G on a surface Σ is a representation of G on Σ in which points of Σ are associated to vertices and simple arcs are associated to edges in such a way that:...

in the plane. By planar duality it became coloring the vertices, and in this form it generalizes to all graphs. In mathematical and computer representations it is typical to use the first few positive or nonnegative integers as the "colors". In general one can use any finite set as the "color set". The nature of the coloring problem depends on the number of colors but not on what they are.

Graph coloring enjoys many practical applications as well as theoretical challenges. Beside the classical types of problems, different limitations can also be set on the graph, or on the way a color is assigned, or even on the color itself. It has even reached popularity with the general public in the form of the popular number puzzle Sudoku

Sudoku

is a logic-based, combinatorial number-placement puzzle. The objective is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 sub-grids that compose the grid contains all of the digits from 1 to 9...

. Graph coloring is still a very active field of research.

Note: Many terms used in this article are defined in Glossary of graph theory
Glossary of graph theory
Graph theory is a growing area in mathematical research, and has a large specialized vocabulary. Some authors use the same word with different meanings. Some authors use different words to mean the same thing. This page attempts to keep up with current usage....

.

History

The first results about graph coloring deal almost exclusively with planar graphs in the form of the coloring of maps.
While trying to color a map of the counties of England, Francis Guthrie

Francis Guthrie

Francis Guthrie was a South African mathematician and botanist who first posed the Four Colour Problem in 1852. At the time, Guthrie was a student of Augustus De Morgan at University College London. He studied under John Lindley, Professor of Botany at the University of London. Guthrie obtained...

postulated the four color conjecture, noting that four colors were sufficient to color the map so that no regions sharing a common border received the same color. Guthrie’s brother passed on the question to his mathematics teacher Augustus de Morgan

Augustus De Morgan

Augustus De Morgan was a British mathematician and logician. He formulated De Morgan's laws and introduced the term mathematical induction, making its idea rigorous. The crater De Morgan on the Moon is named after him....

at University College

University College London

University College London is a public research university located in London, United Kingdom and the oldest and largest constituent college of the federal University of London...

, who mentioned it in a letter to William Hamilton

William Rowan Hamilton

Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...

in 1852. Arthur Cayley

Arthur Cayley

Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....

raised the problem at a meeting of the London Mathematical Society

London Mathematical Society

-See also:* American Mathematical Society* Edinburgh Mathematical Society* European Mathematical Society* List of Mathematical Societies* Council for the Mathematical Sciences* BCS-FACS Specialist Group-External links:* * *...

in 1879. The same year, Alfred Kempe

Alfred Kempe

Sir Alfred Bray Kempe D.C.L. F.R.S. was a mathematician best known for his work on linkages and the four color theorem....

published a paper that claimed to establish the result, and for a decade the four color problem was considered solved. For his accomplishment Kempe was elected a Fellow of the Royal Society

Royal Society

The Royal Society of London for Improving Natural Knowledge, known simply as the Royal Society, is a learned society for science, and is possibly the oldest such society in existence. Founded in November 1660, it was granted a Royal Charter by King Charles II as the "Royal Society of London"...

and later President of the London Mathematical Society.

In 1890, Heawood pointed out that Kempe’s argument was wrong. However, in that paper he proved the five color theorem

Five color theorem

The five color theorem is a result from graph theory that given a plane separated into regions, such as a political map of the counties of a state, the regions may be colored using no more than five colors in such a way that no two adjacent regions receive the same color.The five color theorem is...

, saying that every planar map can be colored with no more than five colors, using ideas of Kempe. In the following century, a vast amount of work and theories were developed to reduce the number of colors to four, until the four color theorem was finally proved in 1976 by Kenneth Appel

Kenneth Appel

Kenneth Ira Appel is a mathematician who in 1976, with colleague Wolfgang Haken at the University of Illinois at Urbana-Champaign, solved one of the most famous problems in mathematics, the four-color theorem...

and Wolfgang Haken

Wolfgang Haken

Wolfgang Haken is a mathematician who specializes in topology, in particular 3-manifolds.In 1976 together with colleague Kenneth Appel at the University of Illinois at Urbana-Champaign, Haken solved one of the most famous problems in mathematics, the four-color theorem...

. Perhaps surprisingly, the proof went back to the ideas of Heawood and Kempe and largely disregarded the intervening developments. The proof of the four color theorem is also noteworthy for being the first major computer-aided proof.

In 1912, George David Birkhoff

George David Birkhoff

-External links:* − from National Academies Press, by Oswald Veblen....

introduced the chromatic polynomial

Chromatic polynomial

The chromatic polynomial is a polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to attack the four color problem. It was generalised to the Tutte...

to study the coloring problems, which was generalised to the Tutte polynomial

Tutte polynomial

The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a polynomial in two variables which plays an important role in graph theory, a branch of mathematics and theoretical computer science...

by Tutte, important structures in algebraic graph theory

Algebraic graph theory

Algebraic graph theory is a branch of mathematics in which algebraic methods are applied to problems about graphs. This is in contrast to geometric, combinatoric, or algorithmic approaches...

. Kempe had already drawn attention to the general, non-planar case in 1879, and many results on generalisations of planar graph coloring to surfaces of higher order followed in the early 20th century.

In 1960, Claude Berge

Claude Berge

Claude Berge was a French mathematician, recognized as one of the modern founders of combinatorics and graph theory. He is particularly remembered for his famous conjectures on perfect graphs and for Berge's lemma, which states that a matching M in a graph G is maximum if and only if there is in...

formulated another conjecture about graph coloring, the strong perfect graph conjecture, originally motivated by an information-theoretic

Information theory

Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...

concept called the zero-error capacity of a graph introduced by Shannon. The conjecture remained unresolved for 40 years, until it was established as the celebrated strong perfect graph theorem in 2002 by Chudnovsky

Maria Chudnovsky

Maria Chudnovsky is an Israeli mathematician. She is professor in the departments of mathematics and of industrial engineering and operations research at Columbia University. She grew up in Russia and Israel, studying at the Technion, and received her Ph.D. in 2003 from Princeton University under...

, Robertson

Neil Robertson (mathematician)

G. Neil Robertson is a mathematician working mainly in topological graph theory, currently a distinguished professor at the Ohio State University. He earned his Ph.D. in 1969 at the University of Waterloo under his doctoral advisor William Tutte. According to the criteria of the Erdős Number...

, Seymour, Thomas

Robin Thomas (mathematician)

Robin Thomas is a mathematician working in graph theory at the Georgia Institute of Technology.Thomas received his doctorate in 1985 from Charles University in Prague, Czechoslovakia , under the supervision of Jaroslav Nešetřil...

2002.

Graph coloring has been studied as an algorithmic problem since the early 1970s: the chromatic number problem is one of Karp’s 21 NP-complete problems from 1972, and at approximately the same time various exponential-time algorithms were developed based on backtracking and on the deletion-contraction recurrence of . One of the major applications of graph coloring, register allocation

In compiler optimization, register allocation is the process of assigning a large number of target program variables onto a small number of CPU registers...

in compilers, was introduced in 1981.

Definition and terminology

Vertex coloring

When used without any qualification, a coloring of a graph is almost always a proper vertex coloring, namely a labelling of the graph’s vertices with colors such that no two vertices sharing the same edge have the same color. Since a vertex with a loop

Loop (graph theory)

In graph theory, a loop is an edge that connects a vertex to itself. A simple graph contains no loops....

could never be properly colored, it is understood that graphs in this context are loopless.

The terminology of using colors for vertex labels goes back to map coloring. Labels like red and blue are only used when the number of colors is small, and normally it is understood that the labels are drawn from the integers {1,2,3,...}.

A coloring using at most k colors is called a (proper) k-coloring.
The smallest number of colors needed to color a graph G is called its chromatic number, χ(G).
A graph that can be assigned a (proper) k-coloring is k-colorable, and it is k-chromatic if its chromatic number is exactly k.
A subset of vertices assigned to the same color is called a color class, every such class forms an independent set

Independent set (graph theory)

In graph theory, an independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I...

. Thus, a k-coloring is the same as a partition of the vertex set into k independent sets, and the terms k-partite and k-colorable have the same meaning.

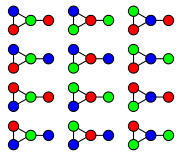
Chromatic polynomial

The chromatic polynomial counts the number of ways a graph can be colored using no more than a given number of colors. For example, using three colors, the graph in the image to the right can be colored in 12 ways. With only two colors, it cannot be colored at all. With four colors, it can be colored in 24 + 4⋅12 = 72 ways: using all four colors, there are 4! = 24 valid colorings (every assignment of four colors to any 4-vertex graph is a proper coloring); and for every choice of three of the four colors, there are 12 valid 3-colorings. So, for the graph in the example, a table of the number of valid colorings would start like this:

Available colors	1	2	3	4	…
Number of colorings	0	0	12	72	…

The chromatic polynomial is a function P(G, t) that counts the number of t-colorings of G. As the name indicates, for a given G the function is indeed a polynomial

Polynomial

In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

in t. For the example graph, P(G, t) = t(t − 1)²(t − 2), and indeed P(G, 4) = 72.

The chromatic polynomial includes at least as much information about the colorability of G as does the chromatic number. Indeed, χ is the smallest positive integer that is not a root of the chromatic polynomial

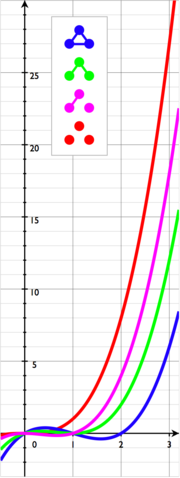
Chromatic polynomials for certain graphs
Triangle K₃
Complete graph Complete graph In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:... K_n
Tree with n vertices
Cycle Cycle graph In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn... C_n
Petersen graph Petersen graph In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...

Edge coloring

An edge coloring of a graph is a proper coloring of the edges, meaning an assignment of colors to edges so that no vertex is incident to two edges of the same color. An edge coloring with k colors is called a k-edge-coloring and is equivalent to the problem of partitioning the edge set into k matchings. The smallest number of colors needed for an edge coloring of a graph G is the chromatic index, or edge chromatic number, χ′(G). A Tait coloring is a 3-edge coloring of a cubic graph

Cubic graph

In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....

. The four color theorem is equivalent to the assertion that every planar cubic bridgeless

Bridge (graph theory)

In graph theory, a bridge is an edge whose deletion increases the number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle....

graph admits a Tait coloring.

Bounds on the chromatic number

Assigning distinct colors to distinct vertices always yields a proper coloring, so

The only graphs that can be 1-colored are edgeless graphs, and the complete graph

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

of n vertices requires

colors. In an optimal coloring there must be at least one of the graph‘s m edges between every pair of color classes, so

If G contains a clique

Clique (graph theory)

In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...

of size k, then at least k colors are needed to color that clique; in other words, the chromatic number is at least the clique number:

For interval graph

Interval graph

In graph theory, an interval graph is the intersection graph of a multiset of intervals on the real line. It has one vertex for each interval in the set, and an edge between every pair of vertices corresponding to intervals that intersect.-Definition:...

s this bound is tight.

The 2-colorable graphs are exactly the bipartite graph

Bipartite graph

In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...

s, including tree

Tree (graph theory)

In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...

s and forests.
By the four color theorem, every planar graph can be 4-colored.

A greedy coloring

Greedy coloring

In the study of graph coloring problems in mathematics and computer science, a greedy coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color...

shows that every graph can be colored with one more color than the maximum vertex degree

Degree (graph theory)

In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...

Complete graphs have

and

, and odd cycles have

and

, so for these graphs this bound is best possible. In all other cases, the bound can be slightly improved; Brooks’ theorem

Brooks’ theorem

In graph theory, Brooks' theorem states a relationship between the maximum degree of a graph and its chromatic number. According to the theorem, in a graph in which every vertex has at most Δ neighbors, the vertices may be colored with only Δ colors, except for two cases, complete graphs and cycle...

states that

Brooks’ theorem:

for a connected, simple graph G, unless G is a complete graph or an odd cycle.

Graphs with high chromatic number

Graphs with large cliques have high chromatic number, but the opposite is not true. The Grötzsch graph

Grötzsch graph

In the mathematical field of graph theory, the Grötzsch graph is a triangle-free graph with 11 vertices, 20 edges, and chromatic number 4. It is named after German mathematician Herbert Grötzsch, and its existence demonstrates that the assumption of planarity is necessary in Grötzsch's theorem ...

is an example of a 4-chromatic graph without a triangle, and the example can be generalised to the Mycielskian

Mycielskian

In the mathematical area of graph theory, the Mycielskian or Mycielski graph of an undirected graph G is a graph μ formed from G by a construction of , who used it to show that there exist triangle-free graphs with arbitrarily large chromatic number.-Construction:Let the n vertices of the given...

Mycielski’s Theorem : There exist triangle-free graphs with arbitrarily high chromatic number.

From Brooks’s theorem, graphs with high chromatic number must have high maximum degree. Another local property that leads to high chromatic number is the presence of a large clique. But colorability is not an entirely local phenomenon: A graph with high girth looks locally like a tree, because all cycles are long, but its chromatic number need not be 2:

Theorem (Erdős): There exist graphs of arbitrarily high girth and chromatic number.

Bounds on the chromatic index

An edge coloring of G is a vertex coloring of its line graph

Line graph

In graph theory, the line graph L of undirected graph G is another graph L that represents the adjacencies between edges of G...

, and vice versa. Thus,

There is a strong relationship between edge colorability and the graph’s maximum degree

. Since all edges incident to the same vertex need their own color, we have

Moreover,

König’s theorem
König's theorem (graph theory)
In the mathematical area of graph theory, König's theorem, proved by Dénes Kőnig in 1931, describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs...

:

if G is bipartite.

In general, the relationship is even stronger than what Brooks’s theorem gives for vertex coloring:

Vizing’s Theorem: A graph of maximal degree

has edge-chromatic number

Other properties

For planar graphs, vertex colorings are essentially dual to nowhere-zero flows

Nowhere-zero flows

In graph theory, nowhere-zero flows are a special type of network flow which is related to coloring planar graphs. Let G = be a directed graph and let M be an abelian group...

.

About infinite graphs, much less is known.
The following is one of the few results about infinite graph coloring:

If all finite subgraphs of an infinite graph G are k-colorable, then so is G, under the assumption of the axiom of choice .

Also, if a graph admits a full n-coloring for every n ≥ n₀, it admits an infinite full coloring .

Open problems

The chromatic number of the plane

Hadwiger–Nelson problem

In geometric graph theory, the Hadwiger–Nelson problem, named after Hugo Hadwiger and Edward Nelson, asks for the minimum number of colors required to color the plane such that no two points at distance one from each other have the same color. The answer is unknown, but has been narrowed down to...

, where two points are adjacent if they have unit distance, is unknown, although it is one of 4, 5, 6, or 7. Other open problems

Unsolved problems in mathematics

This article lists some unsolved problems in mathematics. See individual articles for details and sources.- Millennium Prize Problems :Of the seven Millennium Prize Problems set by the Clay Mathematics Institute, six have yet to be solved:* P versus NP...

concerning the chromatic number of graphs include the Hadwiger conjecture

Hadwiger conjecture (graph theory)

In graph theory, the Hadwiger conjecture states that, if all proper colorings of an undirected graph G use k or more colors, then one can find k disjoint connected subgraphs of G such that each subgraph is connected by an edge to each other subgraph...

stating that every graph with chromatic number k has a complete graph

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

on k vertices as a minor, the Erdős–Faber–Lovász conjecture

Erdos–Faber–Lovász conjecture

In graph theory, the Erdős–Faber–Lovász conjecture is an unsolved problem about graph coloring, named after Paul Erdős, Vance Faber, and László Lovász, who formulated it in 1972...

bounding the chromatic number of unions of complete graphs that have at exactly one vertex in common to each pair, and the Albertson conjecture

Albertson conjecture

In combinatorial mathematics, the Albertson conjecture is an unproven relationship between the crossing number and the chromatic number of a graph. It is named after Michael O. Albertson, a professor at Smith College, who stated it as a conjecture in 2007; it is one of many conjectures made by...

that among k-chromatic graphs the complete graphs are the ones with smallest crossing number

Crossing number (graph theory)

In graph theory, the crossing number cr of a graph G is the lowest number of edge crossings of a planar drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero.The concept originated in...

.

When Birkhoff and Lewis introduced the chromatic polynomial in their attack on the four-color theorem, they conjectured that for planar graphs G, the polymomial

has no zeros in the region

. Although it is known that such a chromatic polynomial has no zeros in the region

and that

, their conjecture is still unresolved. It also remains an unsolved problem to characterize graphs which have the same chromatic polynomial and to determine which polynomials are chromatic.

Algorithms

cellspacing="5" style="width: 22em; text-align: left; font-size: 88%; line-height: 1.5em; ">

Graph coloring

Decision
Name	Graph coloring, vertex coloring, k-coloring
Input	Graph G with n vertices. Integer k
Output	Does G admit a proper vertex coloring with k colors?
Running time	O(2ⁿn)
Complexity	NP-complete NP-complete In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
Reduction from	3-Satisfiability 3sat 3sat is the name of a public, advertising-free, television network in Central Europe. The programming is in German and is broadcast primarily within Germany, Austria and Switzerland .3sat was established for cultural...
Garey–Johnson	GT4
Optimisation
Name	Chromatic number
Input	Graph G with n vertices.
Output	χ(G)
Complexity	NP-hard NP-hard NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
Approximability	O(n (log n)⁻³(log log n)²)
Inapproximability	O(n^1−ε) unless P = NP
Counting problem
Name	Chromatic polymomial
Input	Graph G with n vertices. Integer k
Output	The number P (G,k) of proper k-colorings of G
Running time	O(2ⁿn)
Complexity	#P-complete
Approximability	FPRAS for restricted cases
Inapproximability	No PTAS Polynomial-time approximation scheme In computer science, a polynomial-time approximation scheme is a type of approximation algorithm for optimization problems .... unless P = NP

Polynomial time

Determining if a graph can be colored with 2 colors is equivalent to determining whether or not the graph is bipartite

Bipartite graph

, and thus computable in linear time using breadth-first search

Breadth-first search

In graph theory, breadth-first search is a graph search algorithm that begins at the root node and explores all the neighboring nodes...

. More generally, the chromatic number and a corresponding coloring of perfect graph

Perfect graph

In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....

s can be computed in polynomial time using semidefinite programming

Semidefinite programming

Semidefinite programming is a subfield of convex optimization concerned with the optimization of a linear objective functionover the intersection of the cone of positive semidefinite matrices with an affine space, i.e., a spectrahedron....

. Closed formulas for chromatic polynomial are known for many classes of graphs, such as forest, chordal graphs, cycles, wheels, and ladders, so these can be evaluated in polynomial time.

Exact algorithms

Brute-force search

In computer science, brute-force search or exhaustive search, also known as generate and test, is a trivial but very general problem-solving technique that consists of systematically enumerating all possible candidates for the solution and checking whether each candidate satisfies the problem's...

for a k-coloring considers every of the

assignments of k colors to n vertices and checks for each if it is legal. To compute the chromatic number and the chromatic polynomial, this procedure is used for every

, impractical for all but the smallest input graphs.

Using dynamic programming

Dynamic programming

In mathematics and computer science, dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. It is applicable to problems exhibiting the properties of overlapping subproblems which are only slightly smaller and optimal substructure...

and a bound on the number of maximal independent set

Maximal independent set

In graph theory, a maximal independent set or maximal stable set is an independent set that is not a subset of any other independent set. That is, it is a set S such that every edge of the graph has at least one endpoint not in S and every vertex not in S has at least one neighbor in S...

s, k-colorability can be decided in time and space

. Using the principle of inclusion–exclusion and Yates

Samuel Yates

Samuel Yates was a mathematician who first described unique primes in the 1980s. In 1984 he began the list of "Largest Known Primes" and coined the name titanic prime for any prime with 1,000 or more decimal digits...

’s algorithm for the fast zeta transform,
k-colorability can be decided in time

for any k. Faster algorithms are known for 3- and 4-colorability, which can be decided in time

and

, respectively.

Contraction

The contraction

of graph G is the graph obtained by identifying the vertices u and v, removing any edges between them, and replacing them with a single vertex w where any edges that were incident on u or v are redirected to w. This operation plays a major role in the analysis of graph coloring.

The chromatic number satisfies the recurrence relation

Recurrence relation

In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....

due to ,
where u and v are nonadjacent vertices,

is the graph with the edge

added. Several algorithms are based on evaluating this recurrence, the resulting computation tree is sometimes called a Zykov tree. The running time is based on the heuristic for choosing the vertices u and v.

The chromatic polynomial satisfies following recurrence relation

where u and v are adjacent vertices and

is the graph with the edge

removed.

represents the number of possible proper colorings of the graph, when the vertices may have same or different colors. The number of proper colorings therefore come from the sum of two graphs. If the vertices u and v have different colors, then we can as well consider a graph, where u and v are adjacent. If u and v have the same colors, we may as well consider a graph, where u and v are contracted. Tutte’s curiosity about which other graph properties satisfied this recurrence led him to discover a bivariate generalization of the chromatic polynomial, the Tutte polynomial

Tutte polynomial

.

The expressions give rise to a recursive procedure, called the deletion–contraction algorithm, which forms the basis of many algorithms for graph coloring. The running time satisfies the same recurrence relation as the Fibonacci numbers, so in the worst case, the algorithm runs in time within a polynomial factor of

. The analysis can be improved to within a polynomial factor of the number

of spanning trees

Spanning tree (mathematics)

In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...

of the input graph.
In practice, branch and bound

Branch and bound

Branch and bound is a general algorithm for finding optimal solutions of various optimization problems, especially in discrete and combinatorial optimization...

strategies and graph isomorphism

Isomorphism

In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...

rejection are employed to avoid some recursive calls, the running time depends on the heuristic used to pick the vertex pair.

Greedy coloring

The greedy algorithm

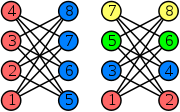
Greedy algorithm

A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....

considers the vertices in a specific order

,…,

and assigns to

the smallest available color not used by

’s neighbours among

,…,

, adding a fresh color if needed. The quality of the resulting coloring depends on the chosen ordering. There exists an ordering that leads to a greedy coloring with the optimal number of

colors. On the other hand, greedy colorings can be arbitrarily bad; for example, the crown graph

Crown graph

In graph theory, a branch of mathematics, a crown graph on 2n vertices is an undirected graph with two sets of vertices ui and vi and with an edge from ui to vj whenever i ≠ j...

on n vertices can be 2-colored, but has an ordering that leads to a greedy coloring with

colors.

If the vertices are ordered according to their degree

Degree (graph theory)

s, the resulting greedy coloring uses at most

colors, at most one more than the graph’s maximum degree. This heuristic is sometimes called the Welsh–Powell algorithm. Another heuristic due to Brélaz

Daniel Brélaz

Daniel Brélaz is a Swiss politician and member of the Green Party of Switzerland.- Biography :Brélaz received a degree in mathematics from EPFL in 1975, and afterwards taught mathematics. He is responsible for a well-known approximation algorithm for graph coloring.In 1975 he joined the Group for...

establishes the ordering dynamically while the algorithm proceeds, choosing next the vertex adjacent to the largest number of different colors. Many other graph coloring heuristics are similarly based on greedy coloring for a specific static or dynamic strategy of ordering the vertices, these algorithms are sometimes called sequential coloring algorithms.

Parallel and distributed algorithms

In the field of distributed algorithms, graph coloring is closely related to the problem of symmetry breaking. The current state-of-the-art randomized algorithms are faster for sufficiently large maximum degree Δ than deterministic algorithms. The fastest randomized algorithms employ the multi-trials technique

Multi-trials technique

The multi-trials technique by Schneider et al. is employed for distributed algorithms and allows to break symmetry efficiently. Symmetry breaking is necessary, for instance, in resource allocation problems, where many entities want to access the same resource concurrently. Many message passing...

by Schneider et al.

In a symmetric graph

Symmetric graph

In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...

, a deterministic

Deterministic algorithm

In computer science, a deterministic algorithm is an algorithm which, in informal terms, behaves predictably. Given a particular input, it will always produce the same output, and the underlying machine will always pass through the same sequence of states...

distributed algorithm cannot find a proper vertex coloring. Some auxiliary information is needed in order to break symmetry. A standard assumption is that initially each node has a unique identifier, for example, from the set {1, 2, ..., n}. Put otherwise, we assume that we are given an n-coloring. The challenge is to reduce the number of colors from n to, e.g., Δ + 1. The more colors are employed, e.g. O(Δ) instead of Δ + 1, the fewer communication rounds are required.

A straightforward distributed version of the greedy algorithm for (Δ + 1)-coloring requires Θ(n) communication rounds in the worst case − information may need to be propagated from one side of the network to another side.

The simplest interesting case is an n-cycle

Cycle graph

In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...

. Richard Cole and Uzi Vishkin

Uzi Vishkin

Uzi Vishkin is a computer scientist at the University of Maryland, College Park, where he is Professor of Electrical and Computer Engineering at the University of Maryland Institute for Advanced Computer Studies . Uzi Vishkin is known for his work in the field of parallel computing...

show that there is a distributed algorithm that reduces the number of colors from n to O(log n) in one synchronous communication step. By iterating the same procedure, it is possible to obtain a 3-coloring of an n-cycle in O( n) communication steps (assuming that we have unique node identifiers).

The function , iterated logarithm

Iterated logarithm

In computer science, the iterated logarithm of n, written n , is the number of times the logarithm function must be iteratively applied before the result is less than or equal to 1...

, is an extremely slowly growing function, "almost constant". Hence the result by Cole and Vishkin raised the question of whether there is a constant-time distribute algorithm for 3-coloring an n-cycle. showed that this is not possible: any deterministic distributed algorithm requires Ω( n) communication steps to reduce an n-coloring to a 3-coloring in an n-cycle.

The technique by Cole and Vishkin can be applied in arbitrary bounded-degree graphs as well; the running time is poly(Δ) + O( n). The technique was extended to unit disk graph

Unit disk graph

In geometric graph theory, a unit disk graph is the intersection graph of a family of unit circles in the Euclidean plane. That is, we form a vertex for each circle, and connect two vertices by an edge whenever the corresponding circles cross each other....

s by Schneider et al. The fastest deterministic algorithms for (Δ + 1)-coloring for small Δ are due to Leonid Barenboim, Michael Elkin and Fabian Kuhn. The algorithm by Barenboim et al. runs in time O(Δ) + (n)/2, which is optimal in terms of n since the constant factor 1/2 cannot be improved due to Linial's lower bound. Panconesi et al. use network decompositions to compute a Δ+1 coloring in time

.

The problem of edge coloring has also been studied in the distributed model. achieve a (2Δ − 1)-coloring in O(Δ + n) time in this model. The lower bound for distributed vertex coloring due to applies to the distributed edge coloring problem as well.

Decentralized algorithms

Decentralized algorithms are ones where no message passing is allowed (in contrast to distributed algorithms where local message passing takes places). Somewhat surprisingly, efficient decentralized algorithms exist that will color a graph if a proper coloring exists. These assume that a vertex is able to sense whether any of its neighbors are using the same color as the vertex i.e., whether a local conflict exists. This is a mild assumption in many applications e.g. in wireless channel allocation it is usually reasonable to assume that a station will be able to detect whether other interfering transmitters are using the same channel (e.g. by measuring the SINR). This sensing information is sufficient to allow algorithms based on learning automata to find a proper graph coloring with probability one, e.g. see and .

Computational complexity

Graph coloring is computationally hard. It is NP-complete

NP-complete

In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...

to decide if a given graph admits a k-coloring for a given k except for the cases k = 1 and k = 2. Especially, it is NP-hard to compute the chromatic number.
The 3-coloring problem remains NP-complete even on planar graph

Planar graph

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...

s of degree 4.

The best known approximation algorithm

Approximation algorithm

In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...

computes a coloring of size at most within a factor O(n(log n)⁻³(log log n)²) of the chromatic number. For all ε > 0, approximating the chromatic number within n^1−ε is NP-hard

NP-hard

NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...

.

It is also NP-hard to color a 3-colorable graph with 4 colors and a k-colorable graph with k^{(log k ) / 25} colors for sufficiently large constant k.

Computing the coefficients of the chromatic polynomial is #P-hard. In fact, even computing the value of

is #P-hard at any rational point k except for k = 1 and k = 2. There is no FPRAS for evaluating the chromatic polynomial at any rational point k ≥ 1.5 except for k = 2 unless NP

NP (complexity)

In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...

= RP

RP (complexity)

In complexity theory, RP is the complexity class of problems for which a probabilistic Turing machine exists with these properties:* It always runs in polynomial time in the input size...

.

For edge coloring, the proof of Vizing’s result gives an algorithm that uses at most Δ+1 colors. However, deciding between the two candidate values for the edge chromatic number is NP-complete. In terms of approximation algorithms, Vizing’s algorithm shows that the edge chromatic number can be approximated within 4/3,
and the hardness result shows that no (4/3 − ε )-algorithm exists for any ε > 0 unless P = NP. These are among the oldest results in the literature of approximation algorithms, even though neither paper makes explicit use of that notion.

Scheduling

Vertex coloring models to a number of scheduling problems. In the cleanest form, a given set of jobs need to be assigned to time slots, each job requires one such slot. Jobs can be scheduled in any order, but pairs of jobs may be in conflict in the sense that they may not be assigned to the same time slot, for example because they both rely on a shared resource. The corresponding graph contains a vertex for every job and an edge for every conflicting pair of jobs. The chromatic number of the graph is exactly the minimum makespan, the optimal time to finish all jobs without conflicts.

Details of the scheduling problem define the structure of the graph. For example, when assigning aircraft to flights, the resulting conflict graph is an interval graph

Interval graph

, so the coloring problem can be solved efficiently. In bandwidth allocation

Bandwidth allocation

Bandwidth allocation refers to how radio frequencies are assigned to different applications. The radio spectrum is a finite resource creating the need for an effective allocation process. In the United States, the Federal Communications Commission or FCC has the responsibility allocating the...

to radio stations, the resulting conflict graph is a unit disk graph

Unit disk graph

, so the coloring problem is 3-approximable.

Register allocation

A compiler

Compiler

A compiler is a computer program that transforms source code written in a programming language into another computer language...

is a computer program

Computer program

A computer program is a sequence of instructions written to perform a specified task with a computer. A computer requires programs to function, typically executing the program's instructions in a central processor. The program has an executable form that the computer can use directly to execute...

that translates one computer language into another. To improve the execution time of the resulting code, one of the techniques of compiler optimization

Compiler optimization

Compiler optimization is the process of tuning the output of a compiler to minimize or maximize some attributes of an executable computer program. The most common requirement is to minimize the time taken to execute a program; a less common one is to minimize the amount of memory occupied...

is register allocation

In compiler optimization, register allocation is the process of assigning a large number of target program variables onto a small number of CPU registers...

, where the most frequently used values of the compiled program are kept in the fast processor registers. Ideally, values are assigned to registers so that they can all reside in the registers when they are used.

The textbook approach to this problem is to model it as a graph coloring problem. The compiler constructs an interference graph, where vertices are symbolic registers and an edge connects two nodes if they are needed at the same time. If the graph can be colored with k colors then the variables can be stored in k registers.

Other applications

The problem of coloring a graph has found a number of applications, including pattern matching

Pattern matching

In computer science, pattern matching is the act of checking some sequence of tokens for the presence of the constituents of some pattern. In contrast to pattern recognition, the match usually has to be exact. The patterns generally have the form of either sequences or tree structures...

.

The recreational puzzle Sudoku

Sudoku

can be seen as completing a 9-coloring on given specific graph with 81 vertices.

Ramsey theory

An important class of improper coloring problems is studied in Ramsey theory

Ramsey theory

Ramsey theory, named after the British mathematician and philosopher Frank P. Ramsey, is a branch of mathematics that studies the conditions under which order must appear...

, where the graph’s edges are assigned to colors, and there is no restriction on the colors of incident edges. A simple example is the friendship theorem says that in any coloring of the edges of

the complete graph of six vertices there will be a monochromatic triangle; often illustrated by saying that any group of six people either has three mutual strangers or three mutual acquaintances. Ramsey theory is concerned with generalisations of this idea to seek regularity amid disorder, finding general conditions for the existence of monochromatic subgraphs with given structure.

Other colorings

List coloring: Each vertex chooses from a list of colors
List edge-coloring:Each edge chooses from a list of colors
Total coloring

Total coloring

In graph theory, total coloring is a type of coloring on the vertices and edges of a graph.When used without any qualification, a total coloring is always assumed to be proper in the sense that no adjacent vertices, no adjacent edges, and no edge and its endvertices are assigned the same color.The...

:Vertices and edges are colored
Harmonious coloring

Harmonious coloring

In graph theory, a harmonious coloring is a vertex coloring in which every pair of colors appears on at most one pair of adjacent vertices...

: Every pair of colors appears on at most one edge
Complete coloring

Complete coloring

In graph theory, complete coloring is the opposite of harmonious coloring in the sense that it is a vertex coloring in which every pair of colors appears on at least one pair of adjacent vertices. Equivalently, a complete coloring is minimal in the sense that it cannot be transformed into a proper...

: Every pair of colors appears on at least one edge
Exact coloring

Exact coloring

In graph theory, an exact coloring is a vertex coloring in which every pair of colors appears on exactly one pair of adjacent vertices. In essence, an exact coloring is a coloring that is both harmonious and complete. Graphs that admit exact colorings have been classified.- External links :* A...

: Every pair of colors appears on exactly one edge
Acyclic coloring

Acyclic coloring

In graph theory, an acyclic coloring is a vertex coloring in which every 2-chromatic subgraph is acyclic.The acyclic chromatic number A of a graph G is the least number of colors needed in any acyclic coloring of G....

: Every 2-chromatic subgraph is acyclic
Star coloring

Star coloring

In graph-theoretic mathematics, a star coloring of a graph G is a vertex coloring in which every path on four vertices uses at least three distinct colors. Equivalently, in a star coloring, the induced subgraphs formed by the vertices of any two colors has connected components that are star graphs...

: Every 2-chromatic subgraph is a disjoint collection of stars

Star (graph theory)

In graph theory, a star Sk is the complete bipartite graph K1,k: a tree with one internal node and k leaves...

Strong coloring

In graph theory, a strong coloring, with respect to a partition of the vertices into subsets of equal sizes, is a vertex coloring in which every color appears exactly once in every partition....

: Every color appears in every partition of equal size exactly once
Strong edge coloring : Edges are colored such that each color class induces a matching (equivalent to coloring the square of the line graph)
Equitable coloring

Equitable coloring

In graph theory, an area of mathematics, an equitable coloring is an assignment of colors to the vertices of an undirected graph, in such a way that*No two adjacent vertices have the same color, and...

: The sizes of color classes differ by at most one
T-coloring : Distance between two colors of adjacent vertices must not belong to fixed set T

Rank coloring : If two vertices have the same color i, then every path between them contain a vertex with color greater than i
Interval edge-coloring : A color of edges meeting in a common vertex must be contiguous
Circular coloring

Circular coloring

In graph theory, circular coloring may be viewed as a refinement of usual graph coloring. The circular chromatic number of a graph G, denoted \chi_c can be given by any of the following definitions, all of which are equivalent .1...

: Motivated by task systems in which production proceeds in a cyclic way
Path coloring

Path coloring

In graph theory, path coloring usually refers to one of two problems:* The problem of coloring a set of paths R in graph G, in such a way that any two paths of R which share an edge in G receive different colors. Set R and graph G are provided at input. This formulation is equivalent to vertex...

: Models a routing problem in graphs
Fractional coloring

Fractional coloring

Fractional coloring is a topic in a young branch of graph theory known as fractional graph theory. It is a generalization of ordinary graph coloring. In a traditional graph coloring, each vertex in a graph is assigned some color, and adjacent vertices — those connected by edges — must be assigned...

: Vertices may have multiple colors, and on each edge the sum of the color parts of each vertex is not greater than one
Oriented coloring

Oriented coloring

In graph theory, oriented graph coloring is a special type of graph coloring. Namely, it isan assignment of "colors" to vertices of an oriented graph that* is proper: no two adjacent vertices get the same color, and...

: Takes into account orientation of edges of the graph
Cocoloring

Cocoloring

In graph theory, a cocoloring of a graph G is an assignment of colors to the vertices such that each color class forms an independent set in G or in the complement of G. The cochromatic number z of G is the least number of colors needed in any cocolorings of G...

: An improper vertex coloring where every color class induces an independent set or a clique
Subcoloring

Subcoloring

In graph theory, a subcoloring is an assignment of colors to a graph's vertices such that each color class induces a vertex disjoint union of cliques....

: An improper vertex coloring where every color class induces a union of cliques
Defective coloring

Defective coloring

In graph theory, a mathematical discipline, defective coloring is a variant of proper vertex coloring. In a proper vertex coloring, the vertices are coloured such that no adjacent vertices have the same colour. In defective coloring, on the other hand, vertices are allowed to have neighbours of the...

: An improper vertex coloring where every color class induces a bounded degree subgraph.
Weak coloring

Weak coloring

In graph theory, a weak coloring is a special case of a graph labeling. A weak -coloring of a graph assigns a color to each vertex , such that each non-isolated vertex is adjacent to at least one vertex with different color. In notation, for each non-isolated , there is a vertex with and .The...

: An improper vertex coloring where every non-isolated node has at least one neighbor with a different color
Sum-coloring : The criterion of minimalization is the sum of colors
Coloring can also be considered for signed graphs and gain graphs.

External links

Graph Coloring Page by Joseph Culberson (graph coloring programs)
CoLoRaTiOn by Jim Andrews and Mike Fellows is a graph coloring puzzle
Links to Graph Coloring source codes
Code for efficiently computing Tutte, Chromatic and Flow Polynomials by Gary Haggard, David J. Pearce and Gordon Royle
Graph Coloring Web Application

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.