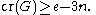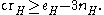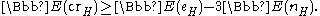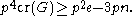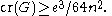Crossing number (graph theory)
Encyclopedia
In graph theory
, the crossing number cr(G) of a graph G is the lowest number of edge crossings of a planar drawing
of the graph G. For instance, a graph is planar
if and only if
its crossing number is zero.
The concept originated in
Turán's brick factory problem, in which Pál Turán
asked to determine the crossing number of the complete bipartite graph
Km,n.
attempted to solve Turán's brick factory problem; his proof contained an error,
but he established a valid upper bound of
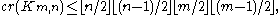
for the crossing number of a complete bipartite graph
Km,n. The conjecture that this inequality is actually an equality is now known as Zarankiewicz' Crossing Number Conjecture.
The problem of determining the crossing number of the complete graph
was first posed by Anthony Hill, and appears in print in 1960. Hill and his collaborator John Ernest
were two constructionist artists
fascinated by mathematics who not only formulated this problem but also originated a conjectural upper bound for this crossing number, which Richard Guy published in 1960. As of March 2009, both problems remain unresolved except for a few special cases; there has been some progress on lower bounds, as reported by .
The Albertson conjecture
, formulated by Michael O. Albertson in 2007, states that, among all graphs with chromatic number n, the complete graph Kn has the minimum number of crossings. That is, if Guy's conjecture on the crossing number of the complete graph is valid, every n-chromatic graph has crossing number at least equal to the formula in the conjecture. It is now known to hold for n ≤ 16.
is essentially the same as the minimum number of convex quadrilaterals determined by a set of n points in general position, closely related to the Happy Ending problem
.
and Johnson
showed in 1983 that it is an NP-hard
problem. In fact the problem remains NP-hard even when restricted to cubic graph
s. More specifically, determining the rectilinear crossing number is complete
for the existential theory of the reals
.
On the positive side, there are efficient algorithms for determining if the crossing number is less than a fixed constant k — in other words, the problem is fixed-parameter tractable. It remains difficult for larger k, such as |V|/2. There are also efficient approximation algorithm
s for approximating cr(G) on graphs of bounded degree. In practice heuristic
algorithms are used, such as the simple algorithm which starts with no edges and continually adds each new edge in a way that produces the fewest additional crossings possible. These algorithms are used in the Rectilinear Crossing Number distributed computing
project.
s with crossing numbers 1–8 are known . The smallest 1-crossing cubic graph is the complete bipartite graph
K3,3, with 6 vertices. The smallest 2-crossing cubic graph is the Petersen graph
, with 10 vertices. The smallest 3-crossing cubic graph is the Heawood graph
, with 14 vertices. The smallest 4-crossing cubic graph is the Möbius-Kantor graph, with 16 vertices. The smallest 5-crossing cubic graph is the Pappus graph
, with 18 vertices. The smallest 6-crossing cubic graph is the Desargues graph
, with 20 vertices. None of the four 7-crossing cubic graphs, with 22 vertices, are well known. The smallest 8-crossing cubic graph is the McGee graph
or (3,7)-cage graph, with 24 vertices.
In 2009, Exoo conjectured that the smallest cubic graph with crossing number 11 is the Coxeter graph
, the smallest cubic graph with crossing number 13 is the Tutte–Coxeter graph and the smallest cubic graph with crossing number 170 is the Tutte 12-cage
.
, Chvátal
, Newborn, and Szemerédi
and by Leighton, asserts that if a graph G (undirected, with no loops or multiple edges) with n vertices and e edges satisfies
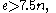
then we have
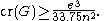
The constant 33.75 is the best known to date,
and is due to Pach and Tóth; the constant 7.5 can be lowered to 4, but at the expense of replacing 33.75 with the worse constant of 64.
The motivation of Leighton in studying crossing numbers was for applications to VLSI design in theoretical
computer science. Later, Székely also realized that this inequality yielded very simple proofs of some important theorems
in incidence geometry
, such as Beck's theorem
and the Szemerédi-Trotter theorem, and Tamal Dey used it to prove upper bounds on geometric k-sets
.
For graphs with girth larger than 2r and e ≥ 4n, Pach, Spencer and Tóth
demonstrated an improvement of this inequality to
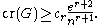
To prove this, consider a diagram of G which has exactly cr(G) crossings. Each of these crossings can be removed
by removing an edge from G. Thus we can find a graph with at least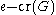
edges and n vertices
with no crossings, and is thus a planar graph
. But from Euler's formula
we must then have
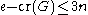, and the claim follows. (In fact we have 
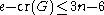for n ≥ 3).
To obtain the actual crossing number inequality, we now use a probabilistic argument
. We let 0 < p < 1 be a probability
parameter to be chosen later, and construct a random subgraph
H of G by allowing each vertex of G to lie in H independently with probability p, and allowing an edge of G to lie in H if and only if its two vertices were chosen to lie in H. Let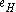
denote the number of edges of H, and let 
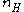denote the number of vertices.
Now consider a diagram of G with cr(G) crossings. We may assume that any two edges in this diagram with a common
vertex are disjoint, otherwise we could interchange the intersecting parts of the two edges and reduce the crossing number by one. Thus every crossing in this diagram involves four distinct vertices of G.
Since H is a subgraph of G, this diagram contains a diagram of H; let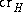
denote the number of crossings of this random graph. By the preliminary crossing number
inequality, we have
Taking expectation
s we obtain
Since each of the n vertices in G had a probability p of being in H, we have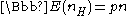
.
Similarly, since each of the edges in G has a probability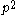
of remaining in H (since both endpoints
need to stay in H), then
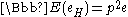. Finally, every crossing in the diagram of G has a probability 
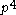of remaining in H, since every crossing involves four vertices, and so 
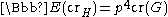. Thus we have
If we now set p to equal 4n/e (which is less than one, since we assume that e is greater than 4n),
we obtain after some algebra
A slight refinement of this argument allows one to replace 64 by 33.75 when e is greater than 7.5 n.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the crossing number cr(G) of a graph G is the lowest number of edge crossings of a planar drawing
Graph drawing
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...
of the graph G. For instance, a graph is planar
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
its crossing number is zero.
The concept originated in
Turán's brick factory problem, in which Pál Turán
Pál Turán
Paul Turán was a Hungarian mathematician who worked primarily in number theory. He had a long collaboration with fellow Hungarian mathematician Paul Erdős, lasting 46 years and resulting in 28 joint papers.- Life and education :...
asked to determine the crossing number of the complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
Km,n.
History
ZarankiewiczKazimierz Zarankiewicz
Kazimierz Zarankiewicz was a Polish mathematician. He was born in Częstochowa and died in London, England.His main interest was topology. He studied at the University of Warsaw, together with Zygmunt Janiszewski, Stefan Mazurkiewicz, Wacław Sierpiński, Kazimierz Kuratowski, and Stanisław Saks...
attempted to solve Turán's brick factory problem; his proof contained an error,
but he established a valid upper bound of
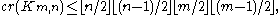
for the crossing number of a complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
Km,n. The conjecture that this inequality is actually an equality is now known as Zarankiewicz' Crossing Number Conjecture.
The problem of determining the crossing number of the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
was first posed by Anthony Hill, and appears in print in 1960. Hill and his collaborator John Ernest
John Ernest
John Ernest was an American-born constructivist abstract artist. He was born in Philadelphia, USA, in 1922. After living and working in Sweden and Paris from 1946 to 1951, he moved to London England where he lived and worked from 1951...
were two constructionist artists
Constructivism (art)
Constructivism was an artistic and architectural philosophy that originated in Russia beginning in 1919, which was a rejection of the idea of autonomous art. The movement was in favour of art as a practice for social purposes. Constructivism had a great effect on modern art movements of the 20th...
fascinated by mathematics who not only formulated this problem but also originated a conjectural upper bound for this crossing number, which Richard Guy published in 1960. As of March 2009, both problems remain unresolved except for a few special cases; there has been some progress on lower bounds, as reported by .
The Albertson conjecture
Albertson conjecture
In combinatorial mathematics, the Albertson conjecture is an unproven relationship between the crossing number and the chromatic number of a graph. It is named after Michael O. Albertson, a professor at Smith College, who stated it as a conjecture in 2007; it is one of many conjectures made by...
, formulated by Michael O. Albertson in 2007, states that, among all graphs with chromatic number n, the complete graph Kn has the minimum number of crossings. That is, if Guy's conjecture on the crossing number of the complete graph is valid, every n-chromatic graph has crossing number at least equal to the formula in the conjecture. It is now known to hold for n ≤ 16.
Variations
Without further qualification, the crossing number allows drawings in which the edges may be represented by arbitrary curves; the rectilinear crossing number requires all edges to be straight line segments, and may differ from the crossing number. In particular, the rectilinear crossing number of a complete graphComplete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
is essentially the same as the minimum number of convex quadrilaterals determined by a set of n points in general position, closely related to the Happy Ending problem
Happy Ending problem
The Happy Ending problem is the following statement:This was one of the original results that led to the development of Ramsey theory....
.
Complexity
In general, determining the crossing number of a graph is hard; GareyMichael Garey
Michael Randolph Garey is a computer science researcher, and co-author of Computers and Intractability: A Guide to the Theory of NP-completeness. He earned his PhD in computer science in 1970 from the University of Wisconsin–Madison. In 1995 he was inducted as a Fellow of the Association for...
and Johnson
David S. Johnson
David Stifler Johnson is a computer scientist specializing in algorithms and optimization. He is currently the head of the Algorithms and Optimization Department of AT&T Labs Research. He was awarded the 2010 Knuth Prize....
showed in 1983 that it is an NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
problem. In fact the problem remains NP-hard even when restricted to cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
s. More specifically, determining the rectilinear crossing number is complete
Complete (complexity)
In computational complexity theory, a computational problem is complete for a complexity class if it is, in a formal sense, one of the "hardest" or "most expressive" problems in the complexity class...
for the existential theory of the reals
Existential theory of the reals
In mathematical logic, computational complexity theory, and computer science, the existential theory of the reals is the set of all true sentences of the form...
.
On the positive side, there are efficient algorithms for determining if the crossing number is less than a fixed constant k — in other words, the problem is fixed-parameter tractable. It remains difficult for larger k, such as |V|/2. There are also efficient approximation algorithm
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
s for approximating cr(G) on graphs of bounded degree. In practice heuristic
Heuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
algorithms are used, such as the simple algorithm which starts with no edges and continually adds each new edge in a way that produces the fewest additional crossings possible. These algorithms are used in the Rectilinear Crossing Number distributed computing
Distributed computing
Distributed computing is a field of computer science that studies distributed systems. A distributed system consists of multiple autonomous computers that communicate through a computer network. The computers interact with each other in order to achieve a common goal...
project.
Crossing numbers of cubic graphs
The smallest cubic graphCubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
s with crossing numbers 1–8 are known . The smallest 1-crossing cubic graph is the complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
K3,3, with 6 vertices. The smallest 2-crossing cubic graph is the Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
, with 10 vertices. The smallest 3-crossing cubic graph is the Heawood graph
Heawood graph
In the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood.-Combinatorial properties:...
, with 14 vertices. The smallest 4-crossing cubic graph is the Möbius-Kantor graph, with 16 vertices. The smallest 5-crossing cubic graph is the Pappus graph
Pappus graph
In the mathematical field of graph theory, the Pappus graph is a 3-regular undirected graph with 18 vertices and 27 edges, formed as the Levi graph of the Pappus configuration. It is named after Pappus of Alexandria, an ancient Greek mathematician who is believed to have discovered the "hexagon...
, with 18 vertices. The smallest 6-crossing cubic graph is the Desargues graph
Desargues graph
In the mathematical field of graph theory, the Desargues graph is a distance-transitive cubic graph with 20 vertices and 30 edges. It is named after Gérard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial...
, with 20 vertices. None of the four 7-crossing cubic graphs, with 22 vertices, are well known. The smallest 8-crossing cubic graph is the McGee graph
McGee graph
In the mathematical field of graph theory, the McGee Graph or the -cage is a 3-regular graph with 24 vertices and 36 edges.The McGeeGraph is the unique -cage . It is also the smallest cubic cage that is not a Moore graph.First discovered by Sachs but unpublished, the graph is named after McGee who...
or (3,7)-cage graph, with 24 vertices.
In 2009, Exoo conjectured that the smallest cubic graph with crossing number 11 is the Coxeter graph
Coxeter graph
In the mathematical field of graph theory, the Coxeter graph is a 3-regular graph with 28 vertices and 42 edges. All the cubic distance-regular graphs are known. The Coxeter graph is one of the 13 such graphs....
, the smallest cubic graph with crossing number 13 is the Tutte–Coxeter graph and the smallest cubic graph with crossing number 170 is the Tutte 12-cage
Tutte 12-cage
In the mathematical field of graph theory, the Tutte 12-cage or Benson graph is a 3-regular graph with 126 vertices and 189 edges named after W. T. Tutte....
.
The crossing number inequality
The very useful crossing number inequality, discovered independently by AjtaiMiklós Ajtai
Miklós Ajtai is a computer scientist at the IBM Almaden Research Center. In 2003 he received the Knuth Prize for his numerous contributions to the field, including a classic sorting network algorithm Miklós Ajtai (born 2 July 1946, Budapest, Hungary) is a computer scientist at the IBM Almaden...
, Chvátal
Chvátal
Chvátal:* Martin Ferdinand Chvátal * Václav "Vašek" Chvátal , a Czech-Canadian mathematician** Chvátal graph** Bondy–Chvátal theorem, named after John Adrian Bondy** Chvatal art gallery theorem...
, Newborn, and Szemerédi
Endre Szemerédi
Endre Szemerédi is a Hungarian mathematician, working in the field of combinatorics and theoretical computer science. He is the State of New Jersey Professor of computer science at Rutgers University since 1986...
and by Leighton, asserts that if a graph G (undirected, with no loops or multiple edges) with n vertices and e edges satisfies
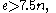
then we have
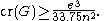
The constant 33.75 is the best known to date,
and is due to Pach and Tóth; the constant 7.5 can be lowered to 4, but at the expense of replacing 33.75 with the worse constant of 64.
The motivation of Leighton in studying crossing numbers was for applications to VLSI design in theoretical
computer science. Later, Székely also realized that this inequality yielded very simple proofs of some important theorems
in incidence geometry
Incidence (geometry)
In geometry, the relations of incidence are those such as 'lies on' between points and lines , and 'intersects' . That is, they are the binary relations describing how subsets meet...
, such as Beck's theorem
Beck's theorem (geometry)
In the context of discrete geometry, Beck's theorem may refer to several different results, two of which are given below. Both appeared, alongside several other important theorems, in a well-known paper by József Beck. The two results described below primarily concern lower bounds on the number of...
and the Szemerédi-Trotter theorem, and Tamal Dey used it to prove upper bounds on geometric k-sets
K-set (geometry)
In discrete geometry, a k-set of a finite point set S in the Euclidean plane is a subset of k elements of S that can be strictly separated from the remaining points by a line. More generally, in Euclidean space of higher dimensions, a k-set of a finite point set is a subset of k elements that can...
.
For graphs with girth larger than 2r and e ≥ 4n, Pach, Spencer and Tóth
demonstrated an improvement of this inequality to
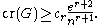
Proof of crossing number inequality
We first give a preliminary estimate: for any graph G with n vertices and e edges, we have
To prove this, consider a diagram of G which has exactly cr(G) crossings. Each of these crossings can be removed
by removing an edge from G. Thus we can find a graph with at least
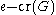edges and n verticeswith no crossings, and is thus a planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
. But from Euler's formula
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
we must then have
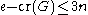, and the claim follows. (In fact we have 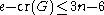for n ≥ 3).To obtain the actual crossing number inequality, we now use a probabilistic argument
Probabilistic method
The probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability that the...
. We let 0 < p < 1 be a probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
parameter to be chosen later, and construct a random subgraph
Random graph
In mathematics, a random graph is a graph that is generated by some random process. The theory of random graphs lies at the intersection between graph theory and probability theory, and studies the properties of typical random graphs.-Random graph models:...
H of G by allowing each vertex of G to lie in H independently with probability p, and allowing an edge of G to lie in H if and only if its two vertices were chosen to lie in H. Let
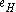denote the number of edges of H, and let 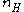denote the number of vertices.Now consider a diagram of G with cr(G) crossings. We may assume that any two edges in this diagram with a common
vertex are disjoint, otherwise we could interchange the intersecting parts of the two edges and reduce the crossing number by one. Thus every crossing in this diagram involves four distinct vertices of G.
Since H is a subgraph of G, this diagram contains a diagram of H; let
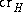denote the number of crossings of this random graph. By the preliminary crossing numberinequality, we have
Taking expectation
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
s we obtain
Since each of the n vertices in G had a probability p of being in H, we have
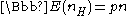.Similarly, since each of the edges in G has a probability
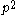of remaining in H (since both endpointsneed to stay in H), then
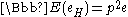. Finally, every crossing in the diagram of G has a probability 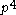of remaining in H, since every crossing involves four vertices, and so 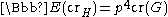. Thus we have
If we now set p to equal 4n/e (which is less than one, since we assume that e is greater than 4n),
we obtain after some algebra
A slight refinement of this argument allows one to replace 64 by 33.75 when e is greater than 7.5 n.