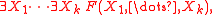Existential theory of the reals
Encyclopedia
In mathematical logic
, computational complexity theory
, and computer science
, the existential theory of the reals
is the set of all true sentences of the form
where F(X1, ..., Xk) is a quantifier-free formula in the language of ordered field
s with coefficients in a real closed field
.
The decision problem
for the existential theory of the reals is the problem of finding an algorithm
that decides, for each such formula, whether it is true or false. This decision problem is NP-hard
and lies in PSPACE
. Thus, it has significantly lower complexity than Alfred Tarski
's quantifier elimination procedure for deciding statements in the first-order theory of the reals without the restriction to existential quantifiers.
may be classified as complete
for the existential theory of the reals. These include:
Based on this, the complexity class
 has been defined as the set of problems having a polynomial-time reduction
has been defined as the set of problems having a polynomial-time reduction
to the existential theory of the reals.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, the existential theory of the reals
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
is the set of all true sentences of the form
where F(X1, ..., Xk) is a quantifier-free formula in the language of ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
s with coefficients in a real closed field
Real closed field
In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
.
The decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
for the existential theory of the reals is the problem of finding an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
that decides, for each such formula, whether it is true or false. This decision problem is NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
and lies in PSPACE
PSPACE
In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :...
. Thus, it has significantly lower complexity than Alfred Tarski
Alfred Tarski
Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
's quantifier elimination procedure for deciding statements in the first-order theory of the reals without the restriction to existential quantifiers.
Complete problems
Several problems in computational complexity and geometric graph theoryGeometric graph theory
In mathematics, a geometric graph is a graph in which the vertices or edges are associated with geometric objects or configurations. Geometric graph theory is a specialization of graph theory that studies geometric graphs...
may be classified as complete
Complete (complexity)
In computational complexity theory, a computational problem is complete for a complexity class if it is, in a formal sense, one of the "hardest" or "most expressive" problems in the complexity class...
for the existential theory of the reals. These include:
- recognition of intersection graphIntersection graphIn the mathematical area of graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph may be represented as an intersection graph, but some important special classes of graphs may be defined by the types of sets that are used to form...
s of line segmentLine segmentIn geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
s in the plane (that is, given an undirected graph, determining whether there is a set of line segments that has an isomorphic intersection graph); - recognition of unit disk graphUnit disk graphIn geometric graph theory, a unit disk graph is the intersection graph of a family of unit circles in the Euclidean plane. That is, we form a vertex for each circle, and connect two vertices by an edge whenever the corresponding circles cross each other....
s (again, given only the graph itself as input); - recognition of intersection graphs of convex sets in the plane;
- stretchability of pseudolines (that is, given a family of curves in the plane, determining whether they are homeomorphic to a line arrangement);
- determining the rectilinear crossing numberCrossing number (graph theory)In graph theory, the crossing number cr of a graph G is the lowest number of edge crossings of a planar drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero.The concept originated in...
of a graph (the minimum number of pairs of edges that cross in any drawing with edges drawn as straight line segments in the plane); - the algorithmic Steinitz problemSteinitz's theoremIn polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...
(given a latticeLattice (order)In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
, determine whether it is the face lattice of a convex polytopeConvex polytopeA convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
); and - testing whether a given graph can be drawn in the plane with a given set of edge pairs as its crossings.\
- testing whether a 4-regular graphRegular graphIn graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
whose edges are coloredEdge coloringIn graph theory, an edge coloring of a graph is an assignment of “colors” to the edges of the graph so that no two adjacent edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several...
with four colors has a drawing with edges as straight line segments of four slopes, with the slopes representing the colors in the coloring.
Based on this, the complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
 has been defined as the set of problems having a polynomial-time reduction
has been defined as the set of problems having a polynomial-time reductionPolynomial-time reduction
In computational complexity theory a polynomial-time reduction is a reduction which is computable by a deterministic Turing machine in polynomial time. If it is a many-one reduction, it is called a polynomial-time many-one reduction, polynomial transformation, or Karp reduction...
to the existential theory of the reals.