
Albertson conjecture
Encyclopedia
In combinatorial
mathematics
, the Albertson conjecture is an unproven relationship between the crossing number
and the chromatic number of a graph. It is named after Michael O. Albertson, a professor at Smith College
, who stated it as a conjecture in 2007; it is one of many conjectures made by Albertson in graph coloring theory. The conjecture states that, among all graphs requiring n colors, the complete graph
Kn is the one with the smallest crossing number.
Equivalently, if a graph can be drawn with fewer crossings than Kn, then, according to the conjecture, it may be colored with fewer than n colors.
It is straightforward to show that graphs with bounded crossing number have bounded chromatic number: one may assign distinct colors to the endpoints of all crossing edges and then 4-color the remaining planar graph
. Albertson's conjecture replaces this qualitative relationship between crossing number and coloring by a more precise quantitative relationship. Specifically,
a different conjecture of states that the crossing number of the complete graph Kn is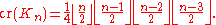
It is known how to draw complete graphs with this many crossings, by placing the vertices in two concentric circles; what is unknown is whether there exists a better drawing with fewer crossings. Therefore, a strengthened formulation of the Albertson conjecture is that every n-chromatic graph has crossing number at least as large as the right hand side of this formula. This strengthened conjecture would be true if and only if both Guy's conjecture and the Albertson conjecture are true.
The Albertson conjecture is vacuously true
for n ≤ 4: K4 has crossing number zero, and all graphs have crossing number greater than or equal to zero. The case n = 5 of Albertson's conjecture is equivalent to the four color theorem
, that any planar graph can be colored with four or fewer colors, for the only graphs requiring fewer crossings than the one crossing of K5 are the planar graphs, and the conjecture implies that these should all be at most 4-chromatic. Through the efforts of several groups of authors the conjecture is now known to hold for all n ≤ 16.
There is also a connection to the Hadwiger conjecture
, an important open problem in combinatorics concerning the relationship between chromatic number and the existence of large cliques
as minors in a graph. A variant of the Hadwiger conjecture, stated by György Hajós, is that every n-chromatic graph contains a subdivision
of Kn; if this were true, the Albertson conjecture would follow, because the crossing number of the whole graph is at least as large as the crossing number of any of its subdivisions. However, counterexamples to the Hajós conjecture are now known, so this connection does not provide an avenue for proof of the Albertson conjecture.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Albertson conjecture is an unproven relationship between the crossing number
Crossing number (graph theory)
In graph theory, the crossing number cr of a graph G is the lowest number of edge crossings of a planar drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero.The concept originated in...
and the chromatic number of a graph. It is named after Michael O. Albertson, a professor at Smith College
Smith College
Smith College is a private, independent women's liberal arts college located in Northampton, Massachusetts. It is the largest member of the Seven Sisters...
, who stated it as a conjecture in 2007; it is one of many conjectures made by Albertson in graph coloring theory. The conjecture states that, among all graphs requiring n colors, the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
Kn is the one with the smallest crossing number.
Equivalently, if a graph can be drawn with fewer crossings than Kn, then, according to the conjecture, it may be colored with fewer than n colors.
It is straightforward to show that graphs with bounded crossing number have bounded chromatic number: one may assign distinct colors to the endpoints of all crossing edges and then 4-color the remaining planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
. Albertson's conjecture replaces this qualitative relationship between crossing number and coloring by a more precise quantitative relationship. Specifically,
a different conjecture of states that the crossing number of the complete graph Kn is
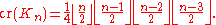
It is known how to draw complete graphs with this many crossings, by placing the vertices in two concentric circles; what is unknown is whether there exists a better drawing with fewer crossings. Therefore, a strengthened formulation of the Albertson conjecture is that every n-chromatic graph has crossing number at least as large as the right hand side of this formula. This strengthened conjecture would be true if and only if both Guy's conjecture and the Albertson conjecture are true.
The Albertson conjecture is vacuously true
Vacuous truth
A vacuous truth is a truth that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true...
for n ≤ 4: K4 has crossing number zero, and all graphs have crossing number greater than or equal to zero. The case n = 5 of Albertson's conjecture is equivalent to the four color theorem
Four color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
, that any planar graph can be colored with four or fewer colors, for the only graphs requiring fewer crossings than the one crossing of K5 are the planar graphs, and the conjecture implies that these should all be at most 4-chromatic. Through the efforts of several groups of authors the conjecture is now known to hold for all n ≤ 16.
There is also a connection to the Hadwiger conjecture
Hadwiger conjecture (graph theory)
In graph theory, the Hadwiger conjecture states that, if all proper colorings of an undirected graph G use k or more colors, then one can find k disjoint connected subgraphs of G such that each subgraph is connected by an edge to each other subgraph...
, an important open problem in combinatorics concerning the relationship between chromatic number and the existence of large cliques
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
as minors in a graph. A variant of the Hadwiger conjecture, stated by György Hajós, is that every n-chromatic graph contains a subdivision
Homeomorphism (graph theory)
In graph theory, two graphs G and G' are homeomorphic if there is an isomorphism from some subdivision of G to some subdivision of G'...
of Kn; if this were true, the Albertson conjecture would follow, because the crossing number of the whole graph is at least as large as the crossing number of any of its subdivisions. However, counterexamples to the Hajós conjecture are now known, so this connection does not provide an avenue for proof of the Albertson conjecture.

