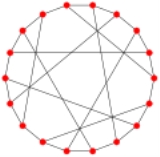
Pappus graph
Encyclopedia
In the mathematical
field of graph theory
, the Pappus graph is a 3-regular
undirected graph with 18 vertices and 27 edges, formed as the Levi graph
of the Pappus configuration. It is named after Pappus of Alexandria
, an ancient Greek mathematician
who is believed to have discovered the "hexagon theorem" describing the Pappus configuration. All the cubic
distance-regular graph
s are known; the Pappus graph is one of the 13 such graphs.
The Pappus graph has rectilinear crossing number
5, and is the smallest cubic graph with that crossing number . It has girth 6, diameter 4, radius 4, chromatic number 2, chromatic index 3 and is both 3-vertex-connected
and 3-edge-connected
.
The Pappus graph has a chromatic polynomial
equal to: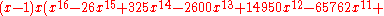

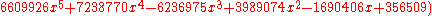 .
.
The name "Pappus graph" has also been used to refer to a related nine-vertex graph, with a vertex for each point of the Pappus configuration and an edge for every pair of points on the same line; this nine-vertex graph is 6-regular, and is the complement graph
of the union of three disjoint triangle graphs.
. It has automorphisms that take any vertex to any other vertex and any edge to any other edge. According to the Foster census, the Pappus graph, referenced as F018A, is the only cubic symmetric graph on 18 vertices.
The characteristic polynomial
of the Pappus graph is . It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
. It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Pappus graph is a 3-regular
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
undirected graph with 18 vertices and 27 edges, formed as the Levi graph
Levi graph
In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for...
of the Pappus configuration. It is named after Pappus of Alexandria
Pappus of Alexandria
Pappus of Alexandria was one of the last great Greek mathematicians of Antiquity, known for his Synagoge or Collection , and for Pappus's Theorem in projective geometry...
, an ancient Greek mathematician
Greek mathematics
Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...
who is believed to have discovered the "hexagon theorem" describing the Pappus configuration. All the cubic
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
distance-regular graph
Distance-regular graph
In mathematics, a distance-regular graph is a regular graph such that for any two vertices v and w at distance i the number of vertices adjacent to w and at distance j from v is the same. Every distance-transitive graph is distance-regular...
s are known; the Pappus graph is one of the 13 such graphs.
The Pappus graph has rectilinear crossing number
Crossing number (graph theory)
In graph theory, the crossing number cr of a graph G is the lowest number of edge crossings of a planar drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero.The concept originated in...
5, and is the smallest cubic graph with that crossing number . It has girth 6, diameter 4, radius 4, chromatic number 2, chromatic index 3 and is both 3-vertex-connected
K-vertex-connected graph
In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
and 3-edge-connected
K-edge-connected graph
In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....
.
The Pappus graph has a chromatic polynomial
Chromatic polynomial
The chromatic polynomial is a polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to attack the four color problem. It was generalised to the Tutte...
equal to:
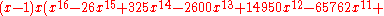

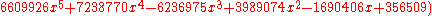 .
.The name "Pappus graph" has also been used to refer to a related nine-vertex graph, with a vertex for each point of the Pappus configuration and an edge for every pair of points on the same line; this nine-vertex graph is 6-regular, and is the complement graph
Complement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
of the union of three disjoint triangle graphs.
Algebraic properties
The automorphism group of the Pappus graph is a group of order 216. It acts transitively on the vertices, on the edges and on the arcs of the graph. Therefore the Pappus graph is a symmetric graphSymmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
. It has automorphisms that take any vertex to any other vertex and any edge to any other edge. According to the Foster census, the Pappus graph, referenced as F018A, is the only cubic symmetric graph on 18 vertices.
The characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the Pappus graph is
 . It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
. It is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.

