K-edge-connected graph
Encyclopedia
In graph theory
, a graph is k-edge-connected if it remains connected
whenever fewer than k edges are removed.
If G = (E \ X,V) is connected for all X ⊆ E where |X| < k, then G is k-edge-connected. Trivially, a graph that is k-edge-connected is also (k−1)-edge-connected.
gives a trivial upper bound on edge-connectivity. That is, if a graph G = (E,V) is k-edge-connected then it is necessary that k ≤ δ(G), where δ(G) is the minimum degree of any vertex v ∈ V. Obviously, deleting all edges incident to a vertex, v, would then disconnect v from the graph.
from u to v with the capacity of all edges in G set to 1 for both directions. A graph is k-edge-connected if and only if the maximum flow from u to v is at least k for any pair (u,v), so k is the least u-v-flow among all (u,v).
If V is the number of vertices in the graph, this simple algorithm would perform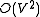
iterations of the Maximum flow problem, which can be solved in 
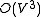time. Hence the complexity of the simple algorithm described above is 
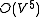in total.
A related problem: finding the minimum k-edge-connected subgraph of G (that is: select as few as possible edges in G that your selection is k-edge-connected) is NP-hard for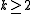
.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a graph is k-edge-connected if it remains connected
Connectivity (graph theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
whenever fewer than k edges are removed.
Formal definition
Let G = (E,V) be an arbitrary graph.If G = (E \ X,V) is connected for all X ⊆ E where |X| < k, then G is k-edge-connected. Trivially, a graph that is k-edge-connected is also (k−1)-edge-connected.
Relation to minimum vertex degree
Minimum vertex degreeDegree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
gives a trivial upper bound on edge-connectivity. That is, if a graph G = (E,V) is k-edge-connected then it is necessary that k ≤ δ(G), where δ(G) is the minimum degree of any vertex v ∈ V. Obviously, deleting all edges incident to a vertex, v, would then disconnect v from the graph.
Computational aspects
There is a polynomial-time algorithm to determine the largest k for which a graph G is k-edge-connected. A simple algorithm would, for every pair (u,v), determine the maximum flowMaximum flow problem
In optimization theory, the maximum flow problem is to find a feasible flow through a single-source, single-sink flow network that is maximum....
from u to v with the capacity of all edges in G set to 1 for both directions. A graph is k-edge-connected if and only if the maximum flow from u to v is at least k for any pair (u,v), so k is the least u-v-flow among all (u,v).
If V is the number of vertices in the graph, this simple algorithm would perform
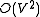iterations of the Maximum flow problem, which can be solved in 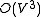time. Hence the complexity of the simple algorithm described above is 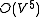in total.A related problem: finding the minimum k-edge-connected subgraph of G (that is: select as few as possible edges in G that your selection is k-edge-connected) is NP-hard for
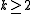.See also
- k-vertex-connected graphK-vertex-connected graphIn graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
- Connectivity (graph theory)Connectivity (graph theory)In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
- Menger's theoremMenger's theoremIn the mathematical discipline of graph theory and related areas, Menger's theorem is a basic result about connectivity in finite undirected graphs. It was proved for edge-connectivity and vertex-connectivity by Karl Menger in 1927...
- Robbins theoremRobbins theoremIn graph theory, a strong orientation of an undirected graph is an assignment of a direction to each edge that makes it into a strongly connected graph. Robbins' theorem, named after , states that the graphs that have strong orientations are exactly the 2-edge-connected graphs...