
Distance-regular graph
Encyclopedia
In mathematics
, a distance-regular graph is a regular
graph
such that for any two vertices v and w at distance
i the number of vertices adjacent to w and at distance j from v is the same. Every distance-transitive graph
is distance-regular. Indeed, distance-regular graphs were introduced as a combinatorial generalization of distance-transitive graphs, having the numerical regularity properties of the latter without necessarily having a large automorphism group
.
Alternatively, a distance-regular graph is a graph for which there exist integers bi,ci,i=0,...,d such that for any two vertices x,y in G and distance i=d(x,y), there are exactly ci neighbors of y in Gi-1(x) and bi neighbors of y in Gi+1(x), where Gi(x) is the set of vertices y of G with d(x,y)=i (Brouwer et al. 1989, p. 434). The array of integers characterizing a distance-regular graph is known as its intersection array.
A distance-regular graph with diameter 2 is strongly regular
, and conversely (unless the graph is disconnected
).
The numbers ai, bi, and ci are often displayed in a three-line array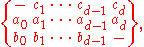
called the intersection array of G. They may also be formed into a tridiagonal matrix
called the intersection matrix.
of Gi. For instance, A1 is the adjacency matrix A of G. Also, let A0 = I, the identity matrix. This gives us d + 1 matrices A0, A1, ..., Ad, called the distance matrices of G. Their sum is the matrix J in which every entry is 1. There is an important product formula: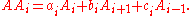
From this formula it follows that each Ai is a polynomial function of A, of degree i, and that A satisfies a polynomial of degree d + 1. Furthermore, A has exactly d + 1 distinct eigenvalues, namely the eigenvalues of the intersection matrix B,of which the largest is k, the degree.
The distance matrices span a vector subspace of the vector space of all n × n real matrices.
It is a remarkable fact that the product Ai Aj of any two distance matrices is a linear combination
of the distance matrices: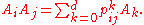
This means that the distance matrices generate an association scheme
. The theory of association schemes is central to the study of distance-regular graphs. For instance, the fact that Ai is a polynomial function of A is a fact about association schemes.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a distance-regular graph is a regular
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
such that for any two vertices v and w at distance
Distance (graph theory)
In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path connecting them. This is also known as the geodesic distance...
i the number of vertices adjacent to w and at distance j from v is the same. Every distance-transitive graph
Distance-transitive graph
In the mathematical field of graph theory, a distance-transitive graph is a graph such that, given any two vertices v and w at any distance i, and any other two vertices x and y at the same distance, there is an automorphism of the graph that carries v to x and w to y.A distance transitive...
is distance-regular. Indeed, distance-regular graphs were introduced as a combinatorial generalization of distance-transitive graphs, having the numerical regularity properties of the latter without necessarily having a large automorphism group
Graph automorphism
In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity....
.
Alternatively, a distance-regular graph is a graph for which there exist integers bi,ci,i=0,...,d such that for any two vertices x,y in G and distance i=d(x,y), there are exactly ci neighbors of y in Gi-1(x) and bi neighbors of y in Gi+1(x), where Gi(x) is the set of vertices y of G with d(x,y)=i (Brouwer et al. 1989, p. 434). The array of integers characterizing a distance-regular graph is known as its intersection array.
A distance-regular graph with diameter 2 is strongly regular
Strongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
, and conversely (unless the graph is disconnected
Connectivity (graph theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
).
Intersection numbers
It is usual to use the following notation for a distance-regular graph G. The number of vertices is n. The number of neighbors of w (that is, vertices adjacent to w) whose distance from v is i, i + 1, and i − 1 is denoted by ai, bi, and ci, respectively; these are the intersection numbers of G. Obviously, a0 = 0, c0 = 0, and b0 equals k, the degree of any vertex. If G has finite diameter, then d denotes the diameter and we have bd = 0. Also we have that ai+bi+ci= kThe numbers ai, bi, and ci are often displayed in a three-line array
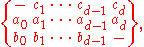
called the intersection array of G. They may also be formed into a tridiagonal matrix

called the intersection matrix.
Distance adjacency matrices
Suppose G is a connected distance-regular graph. For each distance i = 1, ..., d, we can form a graph Gi in which vertices are adjacent if their distance in G equals i. Let Ai be the adjacency matrixAdjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
of Gi. For instance, A1 is the adjacency matrix A of G. Also, let A0 = I, the identity matrix. This gives us d + 1 matrices A0, A1, ..., Ad, called the distance matrices of G. Their sum is the matrix J in which every entry is 1. There is an important product formula:
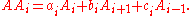
From this formula it follows that each Ai is a polynomial function of A, of degree i, and that A satisfies a polynomial of degree d + 1. Furthermore, A has exactly d + 1 distinct eigenvalues, namely the eigenvalues of the intersection matrix B,of which the largest is k, the degree.
The distance matrices span a vector subspace of the vector space of all n × n real matrices.
It is a remarkable fact that the product Ai Aj of any two distance matrices is a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the distance matrices:
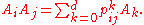
This means that the distance matrices generate an association scheme
Association scheme
The theory of association schemes arose in statistics, in the theory of experimental design for the analysis of variance. In mathematics, association schemes belong to both algebra and combinatorics. Indeed, in algebraic combinatorics, association schemes provide a unified approach to many topics,...
. The theory of association schemes is central to the study of distance-regular graphs. For instance, the fact that Ai is a polynomial function of A is a fact about association schemes.
Examples
- Complete graphComplete graphIn the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
s are distance-regular with diameter 1 and degree v−1. - CycleCycle graphIn graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
s C2d+1 of odd length are distance-regular with k = 2 and diameter d. The intersection numbers ai = 0, bi = 1, and ci = 1, except for the usual special cases (see above) and cd = 2. - All Moore graphs, in particular the Petersen graphPetersen graphIn the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
and the Hoffman-Singleton graphHoffman-Singleton graphIn the mathematical field of graph theory, the Hoffman–Singleton graph is a 7-regular undirected graph with 50 vertices and 175 edges. It is the unique strongly regular graph with parameters . It was constructed by Alan Hoffman and Robert Singleton while trying to classify all Moore graphs, and is...
, are distance-regular. - Strongly regular graphStrongly regular graphIn graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
s are distance-regular. - The odd graphOdd graphIn the mathematical field of graph theory, the odd graphs On are a family of symmetric graphs with high odd girth, defined from certain set systems. They include and generalize the Petersen graph.-Definition and examples:...
s are distance-regular.

