Tridiagonal matrix
Encyclopedia
In linear algebra
, a tridiagonal matrix is a matrix that has nonzero elements only in the main diagonal, the first diagonal below this, and the first diagonal above the main diagonal.
For example, the following matrix is tridiagonal: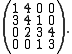
The determinant
of a tridiagonal matrix is given by a continuant
of its elements.
Determining an orthogonal transformation to tridiagonal form can be done with the Lanczos algorithm
.
; in particular, a tridiagonal matrix is a direct sum
of p 1-by-1 and q 2-by-2 matrices such that p + q/2 = n -- the dimension of the tridiagonal. Although a general tridiagonal matrix is not necessarily symmetric or Hermitian, many of those that arise when solving linear algebra problems have one of these properties. Furthermore, if a real tridiagonal matrix A satisfies ak,k+1 ak+1,k > 0, so that the signs of its entries are symmetric, then it is similar to a Hermitian matrix, and hence, its eigenvalues are real. The latter conclusion continues to hold if we replace the condition ak,k+1 ak+1,k > 0 by ak,k+1 ak+1,k ≥ 0.
The set of all n × n tridiagonal matrices forms a 3n-2
dimensional vector space
.
Many linear algebra algorithm
s require significantly less computational effort
when applied to diagonal matrices, and this improvement often carries over to tridiagonal matrices as well. For instance, the determinant
of a tridiagonal matrix A of order n can be computed by the recursive
formula for a continuant
where det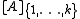
denotes the kth principal minor
, that is,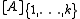
is the submatrix formed by the first k rows and columns of A. The cost of computing the determinant of a tridiagonal matrix using this formula is linear in n, while the cost is cubic for a general matrix.
s, when applied to a Hermitian matrix, reduce the input Hermitian matrix to tridiagonal form as a first step.
A tridiagonal matrix can also be stored more efficiently than a general matrix by using a special storage scheme
. For instance, the LAPACK
Fortran
package stores an unsymmetric tridiagonal matrix of order n in three one-dimensional arrays, one of length n containing the diagonal elements, and two of length n − 1 containing the subdiagonal and superdiagonal elements.
A system of tridiagonal matrix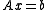
, for 
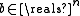can be solved by a specific algorithm called Tridiagonal matrix algorithm
, requiring O(n) operations (Golub and Van Loan).
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a tridiagonal matrix is a matrix that has nonzero elements only in the main diagonal, the first diagonal below this, and the first diagonal above the main diagonal.
For example, the following matrix is tridiagonal:
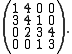
The determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of a tridiagonal matrix is given by a continuant
Continuant (mathematics)
In algebra, the continuant is a multivariate polynomial representing the determinant of a tridiagonal matrix and having applications in generalized continued fractions.-Definition:...
of its elements.
Determining an orthogonal transformation to tridiagonal form can be done with the Lanczos algorithm
Lanczos algorithm
The Lanczos algorithm is an iterative algorithm invented by Cornelius Lanczos that is an adaptation of power methods to find eigenvalues and eigenvectors of a square matrix or the singular value decomposition of a rectangular matrix. It is particularly useful for finding decompositions of very...
.
Properties
A tridiagonal matrix is of Hessenberg typeHessenberg matrix
In linear algebra, a Hessenberg matrix is a special kind of square matrix, one that is "almost" triangular. To be exact, an upper Hessenberg matrix has zero entries below the first subdiagonal, and a lower Hessenberg matrix has zero entries above the first superdiagonal...
; in particular, a tridiagonal matrix is a direct sum
Direct sum
In mathematics, one can often define a direct sum of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets , together with a suitably defined structure. More abstractly, the direct sum is often, but not always, the coproduct in the category in question...
of p 1-by-1 and q 2-by-2 matrices such that p + q/2 = n -- the dimension of the tridiagonal. Although a general tridiagonal matrix is not necessarily symmetric or Hermitian, many of those that arise when solving linear algebra problems have one of these properties. Furthermore, if a real tridiagonal matrix A satisfies ak,k+1 ak+1,k > 0, so that the signs of its entries are symmetric, then it is similar to a Hermitian matrix, and hence, its eigenvalues are real. The latter conclusion continues to hold if we replace the condition ak,k+1 ak+1,k > 0 by ak,k+1 ak+1,k ≥ 0.
The set of all n × n tridiagonal matrices forms a 3n-2
dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
.
Many linear algebra algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s require significantly less computational effort
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
when applied to diagonal matrices, and this improvement often carries over to tridiagonal matrices as well. For instance, the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of a tridiagonal matrix A of order n can be computed by the recursive
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
formula for a continuant
Continuant (mathematics)
In algebra, the continuant is a multivariate polynomial representing the determinant of a tridiagonal matrix and having applications in generalized continued fractions.-Definition:...
where det
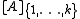denotes the kth principal minorMinor (linear algebra)
In linear algebra, a minor of a matrix A is the determinant of some smaller square matrix, cut down from A by removing one or more of its rows or columns...
, that is,
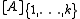is the submatrix formed by the first k rows and columns of A. The cost of computing the determinant of a tridiagonal matrix using this formula is linear in n, while the cost is cubic for a general matrix.Computer programming
A transformation that reduces a general matrix to Hessenberg form will reduce a Hermitian matrix to tridiagonal form. So, many eigenvalue algorithmEigenvalue algorithm
In linear algebra, one of the most important problems is designing efficient and stable algorithms for finding the eigenvalues of a matrix. These eigenvalue algorithms may also find eigenvectors.-Characteristic polynomial:...
s, when applied to a Hermitian matrix, reduce the input Hermitian matrix to tridiagonal form as a first step.
A tridiagonal matrix can also be stored more efficiently than a general matrix by using a special storage scheme
Matrix representation
Matrix representation is a method used by a computer language to store matrices of more than one dimension in memory.Fortran and C use different schemes. Fortran uses "Column Major", in which all the elements for a given column are stored contiguously in memory...
. For instance, the LAPACK
LAPACK
-External links:* : a modern replacement for PLAPACK and ScaLAPACK* on Netlib.org* * * : a modern replacement for LAPACK that is MultiGPU ready* on Sourceforge.net* * optimized LAPACK for Solaris OS on SPARC/x86/x64 and Linux* * *...
Fortran
Fortran
Fortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
package stores an unsymmetric tridiagonal matrix of order n in three one-dimensional arrays, one of length n containing the diagonal elements, and two of length n − 1 containing the subdiagonal and superdiagonal elements.
A system of tridiagonal matrix
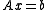, for 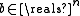can be solved by a specific algorithm called Tridiagonal matrix algorithmTridiagonal matrix algorithm
In numerical linear algebra, the tridiagonal matrix algorithm , also known as the Thomas algorithm , is a simplified form of Gaussian elimination that can be used to solve tridiagonal systems of equations...
, requiring O(n) operations (Golub and Van Loan).
External links
- Tridiagonal and Bidiagonal Matrices in the LAPACK manual.
- Module for Tri-Diagonal Linear Systems
- High performance algorithms for reduction to condensed (Hessenberg, tridiagonal, bidiagonal) form