
Lanczos algorithm
Encyclopedia
The Lanczos algorithm is an iterative algorithm invented by Cornelius Lanczos
that is an adaptation of power methods
to find eigenvalues and eigenvectors of a square matrix or the singular value decomposition
of a rectangular matrix. It is particularly useful for finding decompositions of very large sparse matrices. In latent semantic indexing
, for instance, matrices relating millions of documents to hundreds of thousands of terms must be reduced to singular-value form.
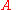 can be summarized by noting that if
can be summarized by noting that if  is a random vector and
is a random vector and  , then in the large
, then in the large  limit,
limit, 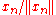 approaches the normed eigenvector corresponding to the largest eigenvalue.
approaches the normed eigenvector corresponding to the largest eigenvalue.
If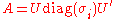 is the eigenvalue decomposition of
is the eigenvalue decomposition of  , then
, then  . As
. As  gets very large, the diagonal matrix of eigenvalues will be dominated by whichever eigenvalue is largest (neglecting the case where there are large equal eigenvalues, of course). As this happens,
gets very large, the diagonal matrix of eigenvalues will be dominated by whichever eigenvalue is largest (neglecting the case where there are large equal eigenvalues, of course). As this happens,  will converge to the largest eigenvalue and
will converge to the largest eigenvalue and  to the associated eigenvector. If the largest eigenvalue is multiple, then
to the associated eigenvector. If the largest eigenvalue is multiple, then 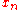 will converge to a vector in the subspace spanned by the eigenvectors associated with those largest eigenvalues. After you get the first eigenvector/value, you can successively restrict the algorithm to the null space of the known eigenvectors to get the other eigenvector/values.
will converge to a vector in the subspace spanned by the eigenvectors associated with those largest eigenvalues. After you get the first eigenvector/value, you can successively restrict the algorithm to the null space of the known eigenvectors to get the other eigenvector/values.
In practice, this simple algorithm does not work very well for computing very many of the eigenvectors because any round-off error
will tend to introduce slight components of the more significant eigenvectors back into the computation, degrading the accuracy of the computation. Pure power methods also can converge slowly, even for the first eigenvector.
 , we also got a series of vectors
, we also got a series of vectors 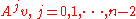 which were eventually discarded. As
which were eventually discarded. As  is often taken to be quite large, this can result in a large amount of disregarded information. More advanced algorithms, such as Arnoldi's algorithm and the Lanczos algorithm, save this information and use the Gram–Schmidt process
is often taken to be quite large, this can result in a large amount of disregarded information. More advanced algorithms, such as Arnoldi's algorithm and the Lanczos algorithm, save this information and use the Gram–Schmidt process
or Householder algorithm to reorthogonalize them into a basis spanning the Krylov subspace
corresponding to the matrix .
.
 'th step of the algorithm transforms the matrix
'th step of the algorithm transforms the matrix  into a tridiagonal matrix
into a tridiagonal matrix  ; when
; when  is equal to the dimension of
is equal to the dimension of  ,
,  is similar to
is similar to  .
.
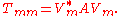
The diagonal elements are denoted by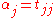 , and the off-diagonal elements are denoted by
, and the off-diagonal elements are denoted by 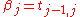 .
.
Note that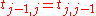 , due to its symmetry.
, due to its symmetry.
There are in principle four ways to write the iteration procedure. Paige[1972] and other works show that the following procedure is the most numerically stable.
 random vector with norm 1.
random vector with norm 1.


Iteration: for
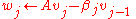
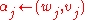


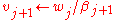
return
Note that (x,y) represents the dot product of vectors x and y here.
After the iteration, we get the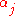 and
and 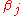 which constructs a tridiagonal matrix
which constructs a tridiagonal matrix

The vectors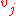 (Lanczos vectors) generated on the fly constructs the transformation matrix
(Lanczos vectors) generated on the fly constructs the transformation matrix
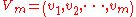 ,
,
which is useful for calculating the eigenvectors (see below). In practice, it could be saved after generation (but takes a lot of memory), or could be regenerated when needed, as long as one keeps the first vector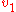 . At each iteration the algorithm executes a matrix-vector multiplication
. At each iteration the algorithm executes a matrix-vector multiplication
and 7n further floating point operations.
 is calculated, one can solve its eigenvalues
is calculated, one can solve its eigenvalues 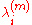 and their corresponding eigenvectors
and their corresponding eigenvectors  (for example, using the QR algorithm
(for example, using the QR algorithm
or Multiple Relatively Robust Representations (MRRR)). The eigenvalues and eigenvectors of can be obtained in as little as
can be obtained in as little as 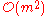 work with MRRR; obtaining just the eigenvalues is much simpler and can be done in
work with MRRR; obtaining just the eigenvalues is much simpler and can be done in 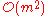 work with spectral bisection.
work with spectral bisection.
It can be proved that the eigenvalues are approximate eigenvalues of the original matrix .
.
The Ritz eigenvectors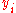 of
of  can be calculated by
can be calculated by 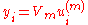 , where
, where 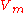 is the transformation matrix whose column vectors are
is the transformation matrix whose column vectors are  .
.
For the Lanczos algorithm, it can be proved that with exact arithmetic, the set of vectors constructs an orthogonal basis, and the eigenvalues/vectors solved are good approximations to those of the original matrix. However, in practice (as the calculations are performed in floating point arithmetic where inaccuracy is inevitable), the orthogonality is quickly lost and in some cases the new vector could even be linearly dependent on the set that is already constructed. As a result, some of the eigenvalues of the resultant tridiagonal matrix may not be approximations to the original matrix. Therefore, the Lanczos algorithm is not very stable.
constructs an orthogonal basis, and the eigenvalues/vectors solved are good approximations to those of the original matrix. However, in practice (as the calculations are performed in floating point arithmetic where inaccuracy is inevitable), the orthogonality is quickly lost and in some cases the new vector could even be linearly dependent on the set that is already constructed. As a result, some of the eigenvalues of the resultant tridiagonal matrix may not be approximations to the original matrix. Therefore, the Lanczos algorithm is not very stable.
Users of this algorithm must be able to find and remove those "spurious" eigenvalues. Practical implementations of the Lanczos algorithm go in three directions to fight this stability issue:
Many implementations of the Lanczos algorithm restart after a certain number of iterations. One of the most influential restarted variations is the implicitly restarted Lanczos method, which is implemented in ARPACK
. This has led into a number of other restarted variations such as restarted Lanczos bidiagonalization. Another successful restarted variation is the Thick-Restart Lanczos method, which has been implemented in a software package called TRLan.
; since the set of people interested in large sparse matrices over finite fields and the set of people interested in large eigenvalue problems scarcely overlap, this is often also called the block Lanczos algorithm without causing unreasonable confusion. See Block Lanczos algorithm for nullspace of a matrix over a finite field
.
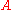 is the only large-scale linear operation. Since weighted-term text retrieval engines implement just this operation, the Lanczos algorithm can be applied efficiently to text documents (see Latent Semantic Indexing
is the only large-scale linear operation. Since weighted-term text retrieval engines implement just this operation, the Lanczos algorithm can be applied efficiently to text documents (see Latent Semantic Indexing
). Eigenvectors are also important for large-scale ranking methods such as the HITS algorithm
developed by Jon Kleinberg
, or the PageRank
algorithm used by Google.
Cornelius Lanczos
Cornelius Lanczos Löwy Kornél was a Hungarian-Jewish mathematician and physicist, who was born on February 2, 1893, and died on June 25, 1974....
that is an adaptation of power methods
Power iteration
In mathematics, the power iteration is an eigenvalue algorithm: given a matrix A, the algorithm will produce a number λ and a nonzero vector v , such that Av = λv....
to find eigenvalues and eigenvectors of a square matrix or the singular value decomposition
Singular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
of a rectangular matrix. It is particularly useful for finding decompositions of very large sparse matrices. In latent semantic indexing
Latent semantic indexing
Latent Semantic Indexing is an indexing and retrieval method that uses a mathematical technique called Singular value decomposition to identify patterns in the relationships between the terms and concepts contained in an unstructured collection of text. LSI is based on the principle that words...
, for instance, matrices relating millions of documents to hundreds of thousands of terms must be reduced to singular-value form.
Power method for finding eigenvalues
The power method for finding the largest eigenvalue of a matrix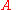 can be summarized by noting that if
can be summarized by noting that if  is a random vector and
is a random vector and  , then in the large
, then in the large  limit,
limit, 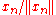 approaches the normed eigenvector corresponding to the largest eigenvalue.
approaches the normed eigenvector corresponding to the largest eigenvalue.If
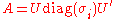 is the eigenvalue decomposition of
is the eigenvalue decomposition of  , then
, then  . As
. As  gets very large, the diagonal matrix of eigenvalues will be dominated by whichever eigenvalue is largest (neglecting the case where there are large equal eigenvalues, of course). As this happens,
gets very large, the diagonal matrix of eigenvalues will be dominated by whichever eigenvalue is largest (neglecting the case where there are large equal eigenvalues, of course). As this happens,  will converge to the largest eigenvalue and
will converge to the largest eigenvalue and  to the associated eigenvector. If the largest eigenvalue is multiple, then
to the associated eigenvector. If the largest eigenvalue is multiple, then 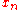 will converge to a vector in the subspace spanned by the eigenvectors associated with those largest eigenvalues. After you get the first eigenvector/value, you can successively restrict the algorithm to the null space of the known eigenvectors to get the other eigenvector/values.
will converge to a vector in the subspace spanned by the eigenvectors associated with those largest eigenvalues. After you get the first eigenvector/value, you can successively restrict the algorithm to the null space of the known eigenvectors to get the other eigenvector/values.In practice, this simple algorithm does not work very well for computing very many of the eigenvectors because any round-off error
Round-off error
A round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...
will tend to introduce slight components of the more significant eigenvectors back into the computation, degrading the accuracy of the computation. Pure power methods also can converge slowly, even for the first eigenvector.
Lanczos method
During the procedure of applying the power method, while getting the ultimate eigenvector , we also got a series of vectors
, we also got a series of vectors 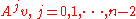 which were eventually discarded. As
which were eventually discarded. As  is often taken to be quite large, this can result in a large amount of disregarded information. More advanced algorithms, such as Arnoldi's algorithm and the Lanczos algorithm, save this information and use the Gram–Schmidt process
is often taken to be quite large, this can result in a large amount of disregarded information. More advanced algorithms, such as Arnoldi's algorithm and the Lanczos algorithm, save this information and use the Gram–Schmidt processGram–Schmidt process
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process is a method for orthonormalising a set of vectors in an inner product space, most commonly the Euclidean space Rn...
or Householder algorithm to reorthogonalize them into a basis spanning the Krylov subspace
Krylov subspace
In linear algebra, the order-r Krylov subspace generated by an n-by-n matrix A and a vector b of dimension n is the linear subspace spanned by the images of b under the first r powers of A , that is,...
corresponding to the matrix
 .
.The algorithm
The Lanczos algorithm can be viewed as a simplified Arnoldi's algorithm in that it applies to Hermitian matrices. The 'th step of the algorithm transforms the matrix
'th step of the algorithm transforms the matrix  into a tridiagonal matrix
into a tridiagonal matrix  ; when
; when  is equal to the dimension of
is equal to the dimension of  ,
,  is similar to
is similar to  .
.Definitions
We hope to calculate the tridiagonal and symmetric matrix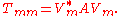
The diagonal elements are denoted by
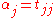 , and the off-diagonal elements are denoted by
, and the off-diagonal elements are denoted by 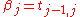 .
.Note that
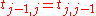 , due to its symmetry.
, due to its symmetry.Iteration
(Note: Following these steps alone will not give you the correct eigenvalue and eigenvectors. More consideration must be applied to correct for the numerical errors. See the section Numerical stability in the following.)There are in principle four ways to write the iteration procedure. Paige[1972] and other works show that the following procedure is the most numerically stable.
 random vector with norm 1.
random vector with norm 1.

Iteration: for

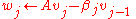
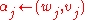


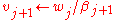
return
Note that (x,y) represents the dot product of vectors x and y here.
After the iteration, we get the
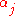 and
and 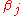 which constructs a tridiagonal matrix
which constructs a tridiagonal matrix
The vectors
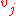 (Lanczos vectors) generated on the fly constructs the transformation matrix
(Lanczos vectors) generated on the fly constructs the transformation matrix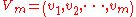 ,
,which is useful for calculating the eigenvectors (see below). In practice, it could be saved after generation (but takes a lot of memory), or could be regenerated when needed, as long as one keeps the first vector
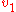 . At each iteration the algorithm executes a matrix-vector multiplication
. At each iteration the algorithm executes a matrix-vector multiplicationand 7n further floating point operations.
Solve for eigenvalues and eigenvectors
After the matrix is calculated, one can solve its eigenvalues
is calculated, one can solve its eigenvalues 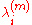 and their corresponding eigenvectors
and their corresponding eigenvectors  (for example, using the QR algorithm
(for example, using the QR algorithmQR algorithm
In numerical linear algebra, the QR algorithm is an eigenvalue algorithm: that is, a procedure to calculate the eigenvalues and eigenvectors of a matrix. The QR transformation was developed in the late 1950s by John G.F. Francis and by Vera N. Kublanovskaya , working independently...
or Multiple Relatively Robust Representations (MRRR)). The eigenvalues and eigenvectors of
 can be obtained in as little as
can be obtained in as little as 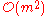 work with MRRR; obtaining just the eigenvalues is much simpler and can be done in
work with MRRR; obtaining just the eigenvalues is much simpler and can be done in 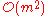 work with spectral bisection.
work with spectral bisection.It can be proved that the eigenvalues are approximate eigenvalues of the original matrix
 .
.The Ritz eigenvectors
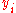 of
of  can be calculated by
can be calculated by 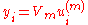 , where
, where 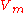 is the transformation matrix whose column vectors are
is the transformation matrix whose column vectors are  .
.Numerical stability
Stability means how much the algorithm will be affected (i.e. will it produce the approximate result close to the original one) if there are small numerical errors introduced and accumulated. Numerical stability is the central criterion for judging the usefulness of implementing an algorithm on a computer with roundoff.For the Lanczos algorithm, it can be proved that with exact arithmetic, the set of vectors
 constructs an orthogonal basis, and the eigenvalues/vectors solved are good approximations to those of the original matrix. However, in practice (as the calculations are performed in floating point arithmetic where inaccuracy is inevitable), the orthogonality is quickly lost and in some cases the new vector could even be linearly dependent on the set that is already constructed. As a result, some of the eigenvalues of the resultant tridiagonal matrix may not be approximations to the original matrix. Therefore, the Lanczos algorithm is not very stable.
constructs an orthogonal basis, and the eigenvalues/vectors solved are good approximations to those of the original matrix. However, in practice (as the calculations are performed in floating point arithmetic where inaccuracy is inevitable), the orthogonality is quickly lost and in some cases the new vector could even be linearly dependent on the set that is already constructed. As a result, some of the eigenvalues of the resultant tridiagonal matrix may not be approximations to the original matrix. Therefore, the Lanczos algorithm is not very stable.Users of this algorithm must be able to find and remove those "spurious" eigenvalues. Practical implementations of the Lanczos algorithm go in three directions to fight this stability issue:
- Prevent the loss of orthogonality
- Recover the orthogonality after the basis is generated
- After the good and "spurious" eigenvalues are all identified, remove the spurious ones.
Variations
Variations on the Lanczos algorithm exist where the vectors involved are tall, narrow matrices instead of vectors and the normalizing constants are small square matrices. These are called "block" Lanczos algorithms and can be much faster on computers with large numbers of registers and long memory-fetch times.Many implementations of the Lanczos algorithm restart after a certain number of iterations. One of the most influential restarted variations is the implicitly restarted Lanczos method, which is implemented in ARPACK
ARPACK
ARPACK, the ARnoldi PACKage, is a numericalsoftware library written in FORTRAN 77 for solving large scale eigenvalue problems.The package is designed to compute a few eigenvalues and corresponding...
. This has led into a number of other restarted variations such as restarted Lanczos bidiagonalization. Another successful restarted variation is the Thick-Restart Lanczos method, which has been implemented in a software package called TRLan.
Nullspace over a finite field
Peter Montgomery published in 1995 an algorithm, based on the Lanczos algorithm, for finding elements of the nullspace of a large sparse matrix over GF(2)GF(2)
GF is the Galois field of two elements. It is the smallest finite field.- Definition :The two elements are nearly always called 0 and 1, being the additive and multiplicative identities, respectively...
; since the set of people interested in large sparse matrices over finite fields and the set of people interested in large eigenvalue problems scarcely overlap, this is often also called the block Lanczos algorithm without causing unreasonable confusion. See Block Lanczos algorithm for nullspace of a matrix over a finite field
Block Lanczos algorithm for nullspace of a matrix over a finite field
The block Lanczos algorithm for nullspace of a matrix over a finite field is a procedure for finding the nullspace of a matrix using only multiplication of the matrix by long, thin matrices...
.
Applications
Lanczos algorithms are very attractive because the multiplication by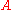 is the only large-scale linear operation. Since weighted-term text retrieval engines implement just this operation, the Lanczos algorithm can be applied efficiently to text documents (see Latent Semantic Indexing
is the only large-scale linear operation. Since weighted-term text retrieval engines implement just this operation, the Lanczos algorithm can be applied efficiently to text documents (see Latent Semantic IndexingLatent semantic indexing
Latent Semantic Indexing is an indexing and retrieval method that uses a mathematical technique called Singular value decomposition to identify patterns in the relationships between the terms and concepts contained in an unstructured collection of text. LSI is based on the principle that words...
). Eigenvectors are also important for large-scale ranking methods such as the HITS algorithm
HITS algorithm
Hyperlink-Induced Topic Search is a link analysis algorithm that rates Web pages, developed by Jon Kleinberg. It was a precursor to PageRank...
developed by Jon Kleinberg
Jon Kleinberg
-External links:**** Stephen Ibaraki*Yury Lifshits,...
, or the PageRank
PageRank
PageRank is a link analysis algorithm, named after Larry Page and used by the Google Internet search engine, that assigns a numerical weighting to each element of a hyperlinked set of documents, such as the World Wide Web, with the purpose of "measuring" its relative importance within the set...
algorithm used by Google.
External links
- Golub and van Loan give very good descriptions of the various forms of Lanczos algorithms in their book Matrix Computations
- Andrew Ng et al., an analysis of PageRank
- Lanczos and conjugate gradient methods B. A. LaMacchia and A. M. Odlyzko, Solving Large Sparse Linear Systems Over Finite Fields
- Matlab comes with ARPACK built-in. Both stored and implicit matrices can be analyzed through the eigs function.
- A Matlab implementation of the above algorithm (note precision issues) is available as apart of the Gaussian Belief Propagation Matlab Package.
- GraphLab GraphLab collaborative filtering library, large scale parallel implementation of Lanczos (in C++) for multicore.

