
Continuant (mathematics)
Encyclopedia
In algebra
, the continuant is a multivariate polynomial representing the determinant
of a tridiagonal matrix and having applications in generalized continued fraction
s.
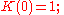
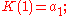

It may also be obtained by taking the sum of all possible products of a1,...,an in which any pairs of consecutive terms are deleted.
An extended definition takes the continuant with respect to three sequences a, b and c, so that K(n) is a polynomial of a1,...,an, b1,...,bn−1 and c1,...,cn−1. In this case the recurrence relation
becomes
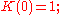
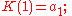
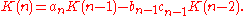
Since br and cr enter into K only as a product brcr there is no loss of generality in assuming that the br are all equal to 1.
of the form . The n-th convergent is
. The n-th convergent is

The extended continuant is precisely the determinant of the tridiagonal matrix

Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, the continuant is a multivariate polynomial representing the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of a tridiagonal matrix and having applications in generalized continued fraction
Generalized continued fraction
In complex analysis, a branch of mathematics, a generalized continued fraction is a generalization of regular continued fractions in canonical form, in which the partial numerators and partial denominators can assume arbitrary real or complex values....
s.
Definition
The n-th continuant, K(n), of a sequence a = a1,...,an,... is defined recursively by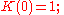
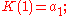

It may also be obtained by taking the sum of all possible products of a1,...,an in which any pairs of consecutive terms are deleted.
An extended definition takes the continuant with respect to three sequences a, b and c, so that K(n) is a polynomial of a1,...,an, b1,...,bn−1 and c1,...,cn−1. In this case the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
becomes
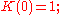
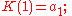
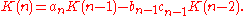
Since br and cr enter into K only as a product brcr there is no loss of generality in assuming that the br are all equal to 1.
Applications
The simple continuant gives the value of a continued fractionContinued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
of the form
 . The n-th convergent is
. The n-th convergent is
The extended continuant is precisely the determinant of the tridiagonal matrix


