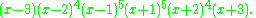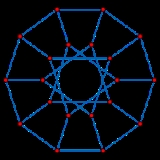
Desargues graph
Encyclopedia
In the mathematical
field of graph theory
, the Desargues graph is a distance-transitive
cubic graph
with 20 vertices and 30 edges. It is named after Gérard Desargues
, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar
cubic partial cube
, and has been applied in chemical databases.
The name "Desargues graph" has also been used to refer to the complement of the Petersen graph
.
: it has symmetries that take any vertex to any other vertex and any edge to any other edge. Its symmetry group has order 240, and is isomorphic to the product of a symmetric group
on 5 points with a group of order 2.
One can interpret this product representation of the symmetry group in terms of the constructions of the Desargues graph: the symmetric group on five points is the symmetry group of the Desargues configuration, and the order-2 subgroup swaps the roles of the vertices that represent points of the Desargues configuration and the vertices that represent lines. Alternatively, in terms of the bipartite Kneser graph, the symmetric group on five points acts separately on the two-element and three-element subsets of the five points, and complementation of subsets forms a group of order two that transforms one type of subset into the other. The symmetric group on five points is also the symmetry group of the Petersen graph, and the order-2 subgroup swaps the vertices within each pair of vertices formed in the double cover construction.
The generalized Petersen graph G(n, k) is vertex-transitive if and only if n = 10 and k = 2 or if k2 ≡ ±1 (mod n) and is edge-transitive only in the following seven cases: (n, k) = (4, 1), (5, 2), (8, 3), (10, 2), (10, 3), (12, 5), (24, 5). So the Desargues graph is one of only seven symmetric Generalized Petersen graphs. Among these seven graphs are the cubical graph
G(4, 1), the Petersen graph
G(5, 2), the Möbius–Kantor graph
G(8, 3), the dodecahedral graph G(10, 2) and the Nauru graph
G(12, 5).
The characteristic polynomial
of the Desargues graph is
Therefore the Desargues graph is an integral graph
: its spectrum
consists entirely of integers.
, the Desargues graph is known as the Desargues–Levi graph; it is used to organize systems of stereoisomers of 5-ligand
compounds. In this application, the thirty edges of the graph correspond to pseudorotation
s of the ligands.
6, and is the smallest cubic graph with that crossing number . It is the only known nonplanar cubic partial cube
.
The Desargues graph has chromatic number 2, chromatic index 3, radius 5, diameter 5 and girth 6. It is also a 3-vertex-connected
and a 3-edge-connected
Hamiltonian graph.
All the cubic
distance-regular graph
s are known. The Desargues graph is one of the 13 such graphs.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Desargues graph is a distance-transitive
Distance-transitive graph
In the mathematical field of graph theory, a distance-transitive graph is a graph such that, given any two vertices v and w at any distance i, and any other two vertices x and y at the same distance, there is an automorphism of the graph that carries v to x and w to y.A distance transitive...
cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
with 20 vertices and 30 edges. It is named after Gérard Desargues
Gérard Desargues
Girard Desargues was a French mathematician and engineer, who is considered one of the founders of projective geometry. Desargues' theorem, the Desargues graph, and the crater Desargues on the Moon are named in his honour.Born in Lyon, Desargues came from a family devoted to service to the French...
, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
cubic partial cube
Partial cube
In graph theory, a partial cube is a graph that is an isometric subgraph of a hypercube. In other words, a partial cube is a subgraph of a hypercube that preserves distances—the distance between any two vertices in the subgraph is the same as the distance between those vertices in the hypercube...
, and has been applied in chemical databases.
The name "Desargues graph" has also been used to refer to the complement of the Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
.
Constructions
There are several different ways of constructing the Desargues graph:- It is the generalized Petersen graphGeneralized Petersen graphIn graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized...
G(10, 3). To form the Desargues graph in this way, connect ten of the vertices into a regular decagonDecagonIn geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°...
, and connect the other ten vertices into a ten-pointed star that connects pairs of vertices at distance three in a second decagon. The Desargue graph consists of the 20 edges of these two polygons together with an additional 10 edges connecting points of one decagon to the corresponding points of the other. - It is the Levi graphLevi graphIn combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for...
of the Desargues configuration. This configuration consists of ten points and ten lines describing two perspective trianglesPerspective (geometry)In geometry, two triangles are perspective if, when the sides of each triangle are extended, they meet at three collinear points. The line which goes through the three points is known as the perspectrix, perspective axis, homology axis, or axis of perspectivity. The triangles are said to be...
, their center of perspectivity, and their axis of perspectivity. The Desargues graph has one vertex for each point, one vertex for each line, and one edge for every incident point-line pair. Desargues' theoremDesargues' theoremIn projective geometry, Desargues' theorem, named in honor of Gérard Desargues, states:Denote the three vertices of one triangle by a, b, and c, and those of the other by A, B, and C...
, named after 17th-century French mathematician Gérard DesarguesGérard DesarguesGirard Desargues was a French mathematician and engineer, who is considered one of the founders of projective geometry. Desargues' theorem, the Desargues graph, and the crater Desargues on the Moon are named in his honour.Born in Lyon, Desargues came from a family devoted to service to the French...
, describes a set of points and lines forming this configuration, and the configuration and the graph take their name from it. - It is the bipartite double coverBipartite double coverIn graph theoretic mathematics, the bipartite double cover of an undirected graph G is a bipartite covering graph of G, with twice as many vertices as G. It can be constructed as the tensor product of graphs G × K2...
of the Petersen graphPetersen graphIn the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
, formed by replacing each Petersen graph vertex by a pair of vertices and each Petersen graph edge by a pair of crossed edges. - It is the bipartite Kneser graphKneser graphIn graph theory, the Kneser graph is the graph whose vertices correspond to the -element subsets of a set of elements, and where two vertices are connected if and only if the two corresponding sets are disjoint...
H5,2. Its vertices can be labeled by the ten two-element subsets and the ten three-element subsets of a five-element set, with an edge connecting two vertices when one of the corresponding sets is a subset of the other. - The Desargues graph is Hamiltonian and can be constructed from the LCF notationLCF notationIn combinatorial mathematics, LCF notation or LCF code is a notation devised by Joshua Lederberg, and extended by Coxeter and Frucht, for the representation of cubic graphs that are Hamiltonian. Since the graphs are Hamiltonian, the vertices can be arranged in a cycle, which accounts for two edges...
: [5,−5,9,−9]5
Algebraic properties
The Desargues graph is a symmetric graphSymmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
: it has symmetries that take any vertex to any other vertex and any edge to any other edge. Its symmetry group has order 240, and is isomorphic to the product of a symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on 5 points with a group of order 2.
One can interpret this product representation of the symmetry group in terms of the constructions of the Desargues graph: the symmetric group on five points is the symmetry group of the Desargues configuration, and the order-2 subgroup swaps the roles of the vertices that represent points of the Desargues configuration and the vertices that represent lines. Alternatively, in terms of the bipartite Kneser graph, the symmetric group on five points acts separately on the two-element and three-element subsets of the five points, and complementation of subsets forms a group of order two that transforms one type of subset into the other. The symmetric group on five points is also the symmetry group of the Petersen graph, and the order-2 subgroup swaps the vertices within each pair of vertices formed in the double cover construction.
The generalized Petersen graph G(n, k) is vertex-transitive if and only if n = 10 and k = 2 or if k2 ≡ ±1 (mod n) and is edge-transitive only in the following seven cases: (n, k) = (4, 1), (5, 2), (8, 3), (10, 2), (10, 3), (12, 5), (24, 5). So the Desargues graph is one of only seven symmetric Generalized Petersen graphs. Among these seven graphs are the cubical graph
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
G(4, 1), the Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
G(5, 2), the Möbius–Kantor graph
Möbius–Kantor graph
In the mathematical field of graph theory, the Möbius–Kantor graph is a symmetric bipartite cubic graph with 16 vertices and 24 edges named after August Ferdinand Möbius and Seligmann Kantor...
G(8, 3), the dodecahedral graph G(10, 2) and the Nauru graph
Nauru graph
In the mathematical field of graph theory, the Nauru graph is a symmetric bipartite cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru....
G(12, 5).
The characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
of the Desargues graph is
Therefore the Desargues graph is an integral graph
Integral graph
In the mathematical field of graph theory, an integral graph is a graph whose spectrum consists entirely of integers. In other words, a graphs is an integral graph if all the eigenvalues of its characteristic polynomial are integers....
: its spectrum
Spectral graph theory
In mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....
consists entirely of integers.
Applications
In chemistryChemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
, the Desargues graph is known as the Desargues–Levi graph; it is used to organize systems of stereoisomers of 5-ligand
Ligand
In coordination chemistry, a ligand is an ion or molecule that binds to a central metal atom to form a coordination complex. The bonding between metal and ligand generally involves formal donation of one or more of the ligand's electron pairs. The nature of metal-ligand bonding can range from...
compounds. In this application, the thirty edges of the graph correspond to pseudorotation
Pseudorotation
The IUPAC defines pseudorotation as "a conformational change resulting in a structure that appears to have been produced by rotation of the entire initial molecule and is superimposable on the initial one, unless different positions are distinguished by substitution or isotopic labeling...
s of the ligands.
Other properties
The Desargues graph has rectilinear crossing numberCrossing number (graph theory)
In graph theory, the crossing number cr of a graph G is the lowest number of edge crossings of a planar drawing of the graph G. For instance, a graph is planar if and only if its crossing number is zero.The concept originated in...
6, and is the smallest cubic graph with that crossing number . It is the only known nonplanar cubic partial cube
Partial cube
In graph theory, a partial cube is a graph that is an isometric subgraph of a hypercube. In other words, a partial cube is a subgraph of a hypercube that preserves distances—the distance between any two vertices in the subgraph is the same as the distance between those vertices in the hypercube...
.
The Desargues graph has chromatic number 2, chromatic index 3, radius 5, diameter 5 and girth 6. It is also a 3-vertex-connected
K-vertex-connected graph
In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...
and a 3-edge-connected
K-edge-connected graph
In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....
Hamiltonian graph.
All the cubic
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
distance-regular graph
Distance-regular graph
In mathematics, a distance-regular graph is a regular graph such that for any two vertices v and w at distance i the number of vertices adjacent to w and at distance j from v is the same. Every distance-transitive graph is distance-regular...
s are known. The Desargues graph is one of the 13 such graphs.