Partial cube
Encyclopedia
In graph theory
, a partial cube is a graph
that is an isometric
subgraph of a hypercube. In other words, a partial cube is a subgraph of a hypercube that preserves distance
s—the distance between any two vertices in the subgraph is the same as the distance between those vertices in the hypercube. Equivalently, a partial cube is a graph whose vertices can be labeled with bit strings of equal length in such a way that the distance between two vertices in the graph is equal to the Hamming distance
between their labels. Such a labeling is called a Hamming labeling; it represents an isometric embedding
of the partial cube into a hypercube.
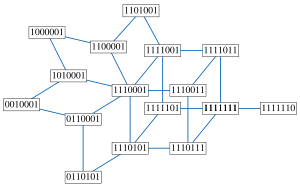The Desargues graph
is a partial cube, as is more generally any bipartite Kneser graph
H. In this bipartite Kneser graph, the labels consist of all possible -digit bitstrings that have either n or nonzero bits; the Desargues graph is constructed in this way with .
All median graph
s are partial cubes. Since the median graphs include the squaregraph
s, simplex graph
s, and Fibonacci cube
s, as well as the covering graphs of finite distributive lattice
s, these are all partial cubes. The planar dual graph of an arrangement of lines
in the Euclidean plane, is a partial cube; more generally, for any hyperplane arrangement in Euclidean space
of any number of dimensions, the graph that has a vertex for each cell of the arrangement and an edge for each two adjacent cells is a partial cube.
A partial cube in which every vertex has exactly three neighbors is known as a cubic
partial cube. Although several infinite families of cubic partial cubes are known, together with many other sporadic examples, the only known cubic partial cube that is not a planar graph
is the Desargues graph.
The underlying graph of any antimatroid
, having a vertex for each set in the antimatroid and an edge for every two sets that differ by a single element, is always a partial cube.
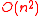time, where 
is the number of vertices in the graph.
defined on the edges of the graph. This relation, first described by and given an equivalent definition in terms of distances by , is denoted by
. Two edges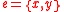 
and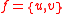 
are defined to be in the relation 
, written 
, if
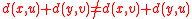. This relation is reflexive
and symmetric
, but in general it is not transitive
.
Winkler showed that a connected
graph is a partial cube if and only if it is bipartite
and the relation
is transitive. In this case, it forms an equivalence relation
and each equivalence class separates two connected subgraphs of the graph from each other. A Hamming labeling may be obtained by assigning one bit of each label to each of the equivalence classes of the Djoković–Winkler relation; in one of the two connected subgraphs separated by an equivalence class of edges, all of the vertices have a 0 in that position of their labels, and in the other connected subgraph all of the vertices have a 1 in the same position.
. A benzenoid graph is a graph consisting of all vertices and edges lying on and in the interior of a cycle in a hexagonal lattice
. Such graphs are the molecular graph
s of the benzenoid hydrocarbons, a large class of organic molecules. Every such graph is a partial cube. A Hamming labeling of such a graph can be used to compute the Wiener index
of the corresponding molecule, which can then be used to predict certain of its chemical properties.
A different molecular structure formed from carbon, the diamond cubic
, also forms partial cube graphs.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a partial cube is a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
that is an isometric
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
subgraph of a hypercube. In other words, a partial cube is a subgraph of a hypercube that preserves distance
Distance (graph theory)
In the mathematical field of graph theory, the distance between two vertices in a graph is the number of edges in a shortest path connecting them. This is also known as the geodesic distance...
s—the distance between any two vertices in the subgraph is the same as the distance between those vertices in the hypercube. Equivalently, a partial cube is a graph whose vertices can be labeled with bit strings of equal length in such a way that the distance between two vertices in the graph is equal to the Hamming distance
Hamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
between their labels. Such a labeling is called a Hamming labeling; it represents an isometric embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
of the partial cube into a hypercube.
Examples
Desargues graph
In the mathematical field of graph theory, the Desargues graph is a distance-transitive cubic graph with 20 vertices and 30 edges. It is named after Gérard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial...
is a partial cube, as is more generally any bipartite Kneser graph
Kneser graph
In graph theory, the Kneser graph is the graph whose vertices correspond to the -element subsets of a set of elements, and where two vertices are connected if and only if the two corresponding sets are disjoint...
H. In this bipartite Kneser graph, the labels consist of all possible -digit bitstrings that have either n or nonzero bits; the Desargues graph is constructed in this way with .
All median graph
Median graph
In mathematics, and more specifically graph theory, a median graph is an undirected graph in which any three vertices a, b, and c have a unique median: a vertex m that belongs to shortest paths between any two of a, b, and c.The concept of median graphs has long been studied, for instance by or ...
s are partial cubes. Since the median graphs include the squaregraph
Squaregraph
In graph theory, a branch of mathematics, a squaregraph is a type of undirected graph that can be drawn in the plane in such a way that every bounded face is a quadrilateral and every vertex with three or fewer neighbors is incident to an unbounded face....
s, simplex graph
Simplex graph
In graph theory, a branch of mathematics, the simplex graph κ of an undirected graph G is itself a graph, with one node for each clique in G...
s, and Fibonacci cube
Fibonacci cube
The Fibonacci cubes or Fibonacci networks are a family of undirected graphs with rich recursive properties derived from its origin in Number Theory. Mathematically they are similar to the hypercube graphs, but with a Fibonacci number of vertices, studied in graph-theoretic mathematics...
s, as well as the covering graphs of finite distributive lattice
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
s, these are all partial cubes. The planar dual graph of an arrangement of lines
Arrangement of lines
In geometry an arrangement of lines is the partition of the plane formed by a collection of lines. Bounds on the complexity of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.-Definition:For any...
in the Euclidean plane, is a partial cube; more generally, for any hyperplane arrangement in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
of any number of dimensions, the graph that has a vertex for each cell of the arrangement and an edge for each two adjacent cells is a partial cube.
A partial cube in which every vertex has exactly three neighbors is known as a cubic
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
partial cube. Although several infinite families of cubic partial cubes are known, together with many other sporadic examples, the only known cubic partial cube that is not a planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
is the Desargues graph.
The underlying graph of any antimatroid
Antimatroid
In mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included...
, having a vertex for each set in the antimatroid and an edge for every two sets that differ by a single element, is always a partial cube.
Recognition
Partial cubes can be recognized, and a Hamming labeling constructed, in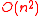 time, where is the number of vertices in the graph.The Djoković–Winkler relation
Many of the theorems about partial cubes, including the recognition algorithm mentioned above, are based directly or indirectly upon a certain binary relationBinary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
defined on the edges of the graph. This relation, first described by and given an equivalent definition in terms of distances by , is denoted by
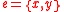. Two edges and 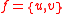are defined to be in the relation , written , if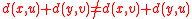. This relation is reflexiveReflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
and symmetric
Symmetric relation
In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
, but in general it is not transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
.
Winkler showed that a connected
Connectivity (graph theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
graph is a partial cube if and only if it is bipartite
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
and the relation
is transitive. In this case, it forms an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
and each equivalence class separates two connected subgraphs of the graph from each other. A Hamming labeling may be obtained by assigning one bit of each label to each of the equivalence classes of the Djoković–Winkler relation; in one of the two connected subgraphs separated by an equivalence class of edges, all of the vertices have a 0 in that position of their labels, and in the other connected subgraph all of the vertices have a 1 in the same position.
Application to chemical graph theory
Isometric embeddings of graphs into hypercubes have an important application in chemical graph theoryChemical graph theory
Chemical graph theory is the topology branch of mathematical chemistry which applies graph theory to mathematical modelling of chemical phenomena....
. A benzenoid graph is a graph consisting of all vertices and edges lying on and in the interior of a cycle in a hexagonal lattice
Hexagonal lattice
The hexagonal lattice or equilateral triangular lattice is one of the five 2D lattice types.Three nearby points form an equilateral triangle. In images four orientations of such a triangle are by far the most common...
. Such graphs are the molecular graph
Molecular graph
In chemical graph theory and in mathematical chemistry, a molecular graph or chemical graph is a representation of the structural formula of a chemical compound in terms of graph theory. A chemical graph is a labeled graph whose vertices correspond to the atoms of the compound and edges correspond...
s of the benzenoid hydrocarbons, a large class of organic molecules. Every such graph is a partial cube. A Hamming labeling of such a graph can be used to compute the Wiener index
Wiener index
In chemical graph theory, the Wiener index is a topological index of a molecule, defined as the sum of the numbers of edges in the shortest paths in a chemical graph between all pairs of non-hydrogen atoms in a molecule. It was introduced by Harry Wiener in 1947. Wiener index may be calculated...
of the corresponding molecule, which can then be used to predict certain of its chemical properties.
A different molecular structure formed from carbon, the diamond cubic
Diamond cubic
The diamond cubic crystal structure is a repeating pattern of 8 atoms that certain materials may adopt as they solidify. While the first known example was diamond, other elements in group IV also adopt this structure, including tin, the semiconductors silicon and germanium, and silicon/germanium...
, also forms partial cube graphs.