In graph theory

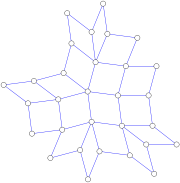
Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, a branch of mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a squaregraph is a type of undirected graph that can be drawn in the plane

Graph drawing

Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...

 in such a way that every bounded face is a quadrilateral

Quadrilateral

In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...

 and every vertex with three or fewer neighbors is incident to an unbounded face.

Characterization

Squaregraphs may be characterized in several ways other than via their planar embeddings:

• They are the median graph
  Median graph
  In mathematics, and more specifically graph theory, a median graph is an undirected graph in which any three vertices a, b, and c have a unique median: a vertex m that belongs to shortest paths between any two of a, b, and c.The concept of median graphs has long been studied, for instance by or ...
  
  s that do not contain as an induced subgraph any member of an infinite family of forbidden graphs. These forbidden graphs are the cube (the simplex graph
  Simplex graph
  In graph theory, a branch of mathematics, the simplex graph κ of an undirected graph G is itself a graph, with one node for each clique in G...
  
   of K₃), the Cartesian product
  Cartesian product of graphs
  In graph theory, the Cartesian product G \square H of graphs G and H is a graph such that* the vertex set of G \square H is the Cartesian product V × V; and...
  
   of an edge and a claw
  Claw (graph theory)
  In graph theory, an area of mathematics, a claw-free graph is a graph that does not have a claw as an induced subgraph.A claw is another name for the complete bipartite graph K1,3...
  
   K_1,3 (the simplex graph of a claw), and the graphs formed from a gear graph by adding one more vertex connected to the hub of the wheel (the simplex graph of the disjoint union of a cycle with an isolated vertex).
• They are the graphs that are connected and bipartite
  Bipartite
  Bipartite means having two parts, or an agreement between two parties. More specifically, it may refer to any of the following:-Mathematics:* 2 * bipartite graph* bipartite cubic, a type of cubic function-Medicine:...
  
  , such that (if an arbitrary vertex r is picked as a root
  Rooted graph
  In mathematics, and, in particular, in graph theory, a rooted graph is a mathematical graph in which one node is labelled in a special way to distinguish it from the graph's other nodes. This special node is called the root of the graph....
  
  ) every vertex has at most two neighbors closer to r, and such that at every vertex v, the link of v (a graph with a vertex for each edge incident to v and an edge for each 4-cycle containing v) is either a cycle of length greater than three or a disjoint union of paths.
• They are the dual graphs of arrangements of lines
  Arrangement of lines
  In geometry an arrangement of lines is the partition of the plane formed by a collection of lines. Bounds on the complexity of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.-Definition:For any...
  
   in the hyperbolic plane
  Hyperbolic space
  In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
  
   that do not have three mutually-crossing lines.

Related graph classes

Squaregraphs are a type of planar

Planar graph

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...

 median graph

Median graph

In mathematics, and more specifically graph theory, a median graph is an undirected graph in which any three vertices a, b, and c have a unique median: a vertex m that belongs to shortest paths between any two of a, b, and c.The concept of median graphs has long been studied, for instance by or ...

; as with median graphs more generally, they are also partial cube

Partial cube

In graph theory, a partial cube is a graph that is an isometric subgraph of a hypercube. In other words, a partial cube is a subgraph of a hypercube that preserves distances—the distance between any two vertices in the subgraph is the same as the distance between those vertices in the hypercube...

s. The squaregraphs include as special cases trees

Tree (graph theory)

In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...

, grid graphs, gear graphs, and the graphs of polyomino

Polyomino

A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling with a connected interior....

s.

Algorithms

The characterization of squaregraphs in terms of distance from a root and links of vertices can be used together with breadth first search as part of a linear time algorithm

Algorithm

In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...

 for testing whether a given graph is a squaregraph, without any need to use the more complex linear-time algorithms for planarity testing

Planarity testing

In graph theory, the planarity testing problem asks whether, given a graph, that graph is a planar graph . This is a well-studied problem in computer science for which many practical algorithms have emerged, many taking advantage of novel data structures...

 of arbitrary graphs.

Several algorithmic problems on squaregraphs may be computed more efficiently than in more general planar or median graphs; for instance, and present linear time algorithms for computing the diameter

Diameter

In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...

of squaregraphs, and for finding a vertex minimizing the maximum distance to all other vertices.