
Claw (graph theory)
Encyclopedia
In graph theory
, an area of mathematics, a claw-free graph is a graph that does not have a claw
as an induced subgraph.
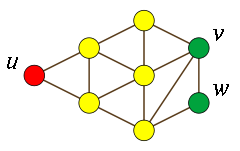
A claw is another name for the complete bipartite graph
K1,3 (that is, a star graph with three edges, three leaves, and one central vertex). A claw-free graph is a graph in which no induced subgraph is a claw; i.e., any subset of four vertices has other than only three edges connecting them in this pattern. Equivalently, a claw-free graph is a graph in which the neighborhood of any vertex
is the complement of a triangle-free graph
.
 Claw-free graphs were initially studied as a generalization of line graph
Claw-free graphs were initially studied as a generalization of line graph
s, and gained additional motivation through three key discoveries about them: the fact that all claw-free connected graphs of even order have perfect matchings, the discovery of polynomial time algorithms for finding maximum independent sets in claw-free graphs, and the characterization of claw-free perfect graph
s. They are the subject of hundreds of mathematical research papers and several surveys.

of its neighbors does not contain a triangle. A graph contains a triangle if and only if the cube of its adjacency matrix
contains a nonzero diagonal element, so finding a triangle may be performed in the same asymptotic time bound as n × n matrix multiplication
. Therefore, using the Coppersmith–Winograd algorithm
, the total time for this claw-free recognition algorithm would be O(n3.376).
observe that in any claw-free graph, each vertex has at most 2√m neighbors; for otherwise by Turán's theorem
the neighbors of the vertex would not have enough remaining edges to form the complement of a triangle-free graph. This observation allows the check of each neighborhood in the fast matrix multiplication based algorithm outlined above to be performed in the same asymptotic time bound as 2√m × 2√m matrix multiplication, or faster for vertices with even lower degrees. The worst case for this algorithm occurs when Ω(√m) vertices have Ω(√m) neighbors each, and the remaining vertices have few neighbors, so its total time is O(m3.376/2) = O(m1.688).
The numbers of connected claw-free graphs on n nodes, for n = 1, 2, ... are
If the graphs are allowed to be disconnected, the numbers of graphs are even larger: they are
A technique of allows the number of claw-free cubic graph
s to be counted very efficiently, unusually for graph enumeration
problems.
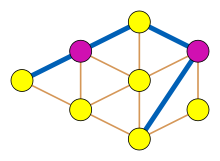
 and, independently, proved that every claw-free connected graph with an even number of vertices has a perfect matching. That is, there exists a set of edges in the graph such that each vertex is an endpoint of exactly one of the matched edges. The special case of this result for line graphs implies that, in any graph with an even number of edges, one can partition the edges into paths of length two. Perfect matchings may be used to provide another characterization of the claw-free graphs: they are exactly the graphs in which every connected induced subgraph of even order has a perfect matching.
and, independently, proved that every claw-free connected graph with an even number of vertices has a perfect matching. That is, there exists a set of edges in the graph such that each vertex is an endpoint of exactly one of the matched edges. The special case of this result for line graphs implies that, in any graph with an even number of edges, one can partition the edges into paths of length two. Perfect matchings may be used to provide another characterization of the claw-free graphs: they are exactly the graphs in which every connected induced subgraph of even order has a perfect matching.
Sumner's proof shows, more strongly, that in any connected claw-free graph one can find a pair of adjacent vertices the removal of which leaves the remaining graph connected. To show this, Sumner finds a pair of vertices u and v that are as far apart as possible in the graph, and chooses w to be a neighbor of v that is as far from u as possible; as he shows, neither v nor w can lie on any shortest path from any other node to u, so the removal of v and w leaves the remaining graph connected. Repeatedly removing matched pairs of vertices in this way forms a perfect matching in the given claw-free graph.
The same proof idea holds more generally if u is any vertex, v is any vertex that is maximally far from u, and w is any neighbor of v that is maximally far from u. Further, the removal of v and w from the graph does not change any of the other distances from u. Therefore, the process of forming a matching by finding and removing pairs vw that are maximally far from u may be performed by a single postorder traversal of a breadth first search tree of the graph, rooted at u, in linear time. provide an alternative linear-time algorithm based on depth-first search
, as well as efficient parallel algorithm
s for the same problem.
list several related results, including the following: (r − 1)-connected K1,r-free graphs of even order have perfect matchings for any r ≥ 2; claw-free graphs of odd order with at most one degree-one vertex may be partitioned into an odd cycle and a matching; for any k that is at most half the minimum degree of a claw-free graph in which either k or the number of vertices is even, the graph has a k-factor; and, if a claw-free graph is (2k + 1)-connected, then any k-edge matching can be extended to a perfect matching.
 An independent set
An independent set
in a line graph corresponds to a matching in its underlying graph, a set of edges no two of which share an endpoint. As showed, a maximum matching in any graph may be found in polynomial time; extended this algorithm to one that computes a maximum independent set in any claw-free graph. (corrected by ) independently provided an alternative extension of Edmonds' algorithms to claw-free graphs, that transforms the problem into one of finding a matching in an auxiliary graph derived from the input claw-free graph. Minty's approach may also be used to solve in polynomial time the more general problem of finding an independent set of maximum weight, and generalizations of these results to wider classes of graphs are also known.
As Sbihi observed, if I is an independent set in a claw-free graph, then any vertex of the graph may have at most two neighbors in I: three neighbors would form a claw. Sbihi calls a vertex saturated if it has two neighbors in I and unsaturated if it is not in I but has fewer than two neighbors in I. It follows from Sbihi's observation that if I and J are both independent sets, the graph induced by I ∪ J must have degree at most two; that is, it is a union of paths and cycles.
In particular, if I is a non-maximum independent set, it differs from any maximum independent set by cycles and augmenting paths, induced path
s which alternate between vertices in I and vertices not in I, and for which both endpoints are unsaturated. The symmetric difference of I with an augmenting path is a larger independent set; Sbihi's algorithm repeatedly increases the size of an independent set by searching for augmenting paths until no more can be found.
Searching for an augmenting path is complicated by the fact that a path may fail to be augmenting if it contains an edge between two vertices that are not in I, so that it is not an induced path. Fortunately, this can only happen in two cases: the two adjacent vertices may be the endpoints of the path, or they may be two steps away from each other; any other adjacency would lead to a claw. Adjacent endpoints may be avoided by temporarily removing the neighbors of v when searching for a path starting from a vertex v; if no path is found, v can be removed from the graph for the remainder of the algorithm. Although Sbihi does not describe it in these terms, the problem remaining after this reduction may be described in terms of a switch graph
, an undirected graph in which the edges incident to each vertex are partitioned into two subsets and in which paths through the vertex are constrained to use one edge from each subset. One may form a switch graph that has as its vertices the unsaturated and saturated vertices of the given claw-free graph, with an edge between two vertices of the switch graph whenever they are nonadjacent in the claw-free graph and there exists a length-two path between them that passes through a vertex of I. The two subsets of edges at each vertex are formed by the two vertices of I that these length-two paths pass through. A path in this switch graph between two unsaturated vertices corresponds to an augmenting path in the original graph. The switch graph has quadratic complexity, paths in it may be found in linear time, and O(n) augmenting paths may need to be found over the course of the overall algorithm. Therefore, Sbihi's algorithm runs in O(n3) total time.
is a graph in which the chromatic number and the size of the maximum clique are equal, and in which this equality persists in every induced subgraph. It is now known (the strong perfect graph theorem) that perfect graphs may be characterized as the graphs that do not have as induced subgraphs either an odd cycle or the complement of an odd cycle (a so-called odd hole). However, for many years this remained an unsolved conjecture, only proven for special subclasses of graphs. One of these subclasses was the family of claw-free graphs: it was discovered by several authors that claw-free graphs without odd cycles and odd holes are perfect. Perfect claw-free graphs may be recognized in polynomial time. In a perfect claw-free graph, the neighborhood of any vertex forms the complement of a bipartite graph
. It is possible to color
perfect claw-free graphs, or to find maximum cliques in them, in polynomial time.
If a claw-free graph is not perfect, it is NP-hard to find to find its largest clique. It is also NP-hard to find an optimal coloring of the graph, because (via line graphs) this problem generalizes the NP-hard problem of computing the chromatic index of a graph. For the same reason, it is NP-hard to find a coloring that achieves an approximation ratio better than 4/3. However, an approximation ratio of two can be achieved by a greedy coloring
algorithm, because the chromatic number of a claw-free graph is greater than half its maximum degree.
Although not every claw-free graph is perfect, claw-free graphs satisfy another property, related to perfection. A graph is called domination perfect if it has a minimum dominating set
that is independent, and if the same property holds in all of its induced subgraphs. Claw-free graphs have this property. To see this, let D be a dominating set in a claw-free graph, and suppose that v and w are two adjacent vertices in D; then the set of vertices dominated by v but not by w must be a clique (else v would be the center of a claw). If every vertex in this clique is already dominated by at least one other member of D, then v can be removed producing a smaller independent dominating set, and otherwise v can be replaced by one of the undominated vertices in its clique producing a dominating set with fewer adjacencies. By repeating this replacement process one eventually reaches a dominating set no larger than D, so in particular when the starting set D is a minimum dominating set this process forms an equally small independent dominating set.
Despite this domination perfectness property, it is NP-hard to determine the size of the minimum dominating set in a claw-free graph. However, in contrast to the situation for more general classes of graphs, finding the minimum dominating set or the minimum connected dominating set in a claw-free graph is fixed-parameter tractable
: it can be solved in time bounded by a polynomial in the size of the graph multiplied by an exponential function of the dominating set size.
for minor-closed graph families proven by Robertson and Seymour, and to the structure theory for perfect graphs that Chudnovsky, Seymour and their co-authors used to prove the strong perfect graph theorem. The theory is too complex to describe in detail here, but to give a flavor of it, it suffices to outline two of their results. First, for a special subclass of claw-free graphs which they call quasi-line graphs (equivalently, locally co-bipartite graphs), they state that every such graph has one of two forms:
Chudnovsky and Seymour classify arbitrary connected claw-free graphs into one of the following:
Much of the work in their structure theory involves a further analysis of antiprismatic graphs. The Schläfli graph
, a claw-free strongly regular graph
with parameters srg(27,16,10,8), plays an important role in this part of the analysis. This structure theory has led to new advances in polyhedral combinatorics
and new bounds on the chromatic number of claw-free graphs, as well as to new fixed-parameter-tractable algorithms for dominating sets in claw-free graphs.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, an area of mathematics, a claw-free graph is a graph that does not have a claw
Claw (graph theory)
In graph theory, an area of mathematics, a claw-free graph is a graph that does not have a claw as an induced subgraph.A claw is another name for the complete bipartite graph K1,3...
as an induced subgraph.
A claw is another name for the complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
K1,3 (that is, a star graph with three edges, three leaves, and one central vertex). A claw-free graph is a graph in which no induced subgraph is a claw; i.e., any subset of four vertices has other than only three edges connecting them in this pattern. Equivalently, a claw-free graph is a graph in which the neighborhood of any vertex
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
is the complement of a triangle-free graph
Triangle-free graph
In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally...
.

Line graph
In graph theory, the line graph L of undirected graph G is another graph L that represents the adjacencies between edges of G...
s, and gained additional motivation through three key discoveries about them: the fact that all claw-free connected graphs of even order have perfect matchings, the discovery of polynomial time algorithms for finding maximum independent sets in claw-free graphs, and the characterization of claw-free perfect graph
Perfect graph
In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....
s. They are the subject of hundreds of mathematical research papers and several surveys.
Examples

- The line graphLine graphIn graph theory, the line graph L of undirected graph G is another graph L that represents the adjacencies between edges of G...
L(G) of any graph G is claw-free; L(G) has a vertex for every edge of G, and vertices are adjacent in L(G) whenever the corresponding edges share an endpoint in G. A line graph L(G) cannot contain a claw, because if three edges e1, e2, and e3 in G all share endpoints with another edge e4 then by the pigeonhole principle at least two of e1, e2, and e3 must share one of those endpoints with each other. Line graphs may be characterized in terms of nine forbidden subgraphs; the claw is the simplest of these nine graphs. This characterization provided the initial motivation for studying claw-free graphs. - The de Bruijn graphDe Bruijn graphIn graph theory, an n-dimensional De Bruijn graph of m symbols is a directed graph representing overlaps between sequences of symbols. It has mn vertices, consisting of all possible length-n sequences of the given symbols; the same symbol may appear multiple times in a sequence...
s (graphs whose vertices represent n-bit binary strings for some n, and whose edges represent (n − 1)-bit overlaps between two strings) are claw-free. One way to show this is via the construction of the de Bruijn graph for n-bit strings as the line graph of the de Bruijn graph for (n − 1)-bit strings. - The complementComplement graphIn graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
of any triangle-free graphTriangle-free graphIn the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally...
is claw-free. These graphs include as a special case any complete graphComplete graphIn the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
. - Proper interval graphs, the interval graphInterval graphIn graph theory, an interval graph is the intersection graph of a multiset of intervals on the real line. It has one vertex for each interval in the set, and an edge between every pair of vertices corresponding to intervals that intersect.-Definition:...
s formed as intersection graphIntersection graphIn the mathematical area of graph theory, an intersection graph is a graph that represents the pattern of intersections of a family of sets. Any graph may be represented as an intersection graph, but some important special classes of graphs may be defined by the types of sets that are used to form...
s of families of intervals in which no interval contains another interval, are claw-free, because four properly intersecting intervals cannot intersect in the pattern of a claw. - The Moser spindleMoser spindleIn graph theory, a branch of mathematics, the Moser spindle is an undirected graph, named after mathematicians Leo Moser and his brother William, with seven vertices and eleven edges...
, a seven-vertex graph used to provide a lower bound for the chromatic number of the planeHadwiger–Nelson problemIn geometric graph theory, the Hadwiger–Nelson problem, named after Hugo Hadwiger and Edward Nelson, asks for the minimum number of colors required to color the plane such that no two points at distance one from each other have the same color. The answer is unknown, but has been narrowed down to...
, is claw-free. - The graphs of several polyhedraPolyhedronIn elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
and polytopePolytopeIn elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
s are claw-free, including the graph of the tetrahedronTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
and more generally of any simplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
(a complete graph), the graph of the octahedronOctahedronIn geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
and more generally of any cross polytope (isomorphicGraph isomorphismIn graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
to the cocktail party graph formed by removing a perfect matching from a complete graph), the graph of the regular icosahedronIcosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
, and the graph of the 16-cell16-cellIn four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....
. - The Schläfli graphSchläfli graphIn the mathematical field of graph theory, the Schläfli graph, named after Ludwig Schläfli, is a 16-regular undirected graph with 27 vertices and 216 edges. It is a strongly regular graph with parameters srg.-Construction:...
, a strongly regular graphStrongly regular graphIn graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
with 27 vertices, is claw-free.
Recognition
It is straightforward to verify that a given graph with n vertices and m edges is claw-free in time O(n4), by testing each 4-tuple of vertices to determine whether they induce a claw. Somewhat more efficiently, but more complicatedly, one can test whether a graph is claw-free by checking, for each vertex of the graph, that the complement graphComplement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
of its neighbors does not contain a triangle. A graph contains a triangle if and only if the cube of its adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
contains a nonzero diagonal element, so finding a triangle may be performed in the same asymptotic time bound as n × n matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. Therefore, using the Coppersmith–Winograd algorithm
Coppersmith–Winograd algorithm
In the mathematical discipline of linear algebra, the Coppersmith–Winograd algorithm, named after Don Coppersmith and Shmuel Winograd, is the asymptotically fastest known algorithm for square matrix multiplication. It can multiply two n \times n matrices in O time...
, the total time for this claw-free recognition algorithm would be O(n3.376).
observe that in any claw-free graph, each vertex has at most 2√m neighbors; for otherwise by Turán's theorem
Turán's theorem
In graph theory, Turán's theorem is a result on the number of edges in a Kr+1-free graph.An n-vertex graph that does not contain any -vertex clique may be formed by partitioning the set of vertices into r parts of equal or nearly-equal size, and connecting two vertices by an edge whenever they...
the neighbors of the vertex would not have enough remaining edges to form the complement of a triangle-free graph. This observation allows the check of each neighborhood in the fast matrix multiplication based algorithm outlined above to be performed in the same asymptotic time bound as 2√m × 2√m matrix multiplication, or faster for vertices with even lower degrees. The worst case for this algorithm occurs when Ω(√m) vertices have Ω(√m) neighbors each, and the remaining vertices have few neighbors, so its total time is O(m3.376/2) = O(m1.688).
Enumeration
Because claw-free graphs include complements of triangle-free graphs, the number of claw-free graphs on n vertices grows at least as quickly as the number of triangle-free graphs, exponentially in the square of n.The numbers of connected claw-free graphs on n nodes, for n = 1, 2, ... are
- 1, 1, 2, 5, 14, 50, 191, 881, 4494, 26389, 184749, ... .
If the graphs are allowed to be disconnected, the numbers of graphs are even larger: they are
- 1, 2, 4, 10, 26, 85, 302, 1285, 6170, ... .
A technique of allows the number of claw-free cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
s to be counted very efficiently, unusually for graph enumeration
Graph enumeration
In combinatorics, an area of mathematics, graph enumeration describes a class of combinatorial enumeration problems in which one must count undirected or directed graphs of certain types, typically as a function of the number of vertices of the graph...
problems.
Matchings

Sumner's proof shows, more strongly, that in any connected claw-free graph one can find a pair of adjacent vertices the removal of which leaves the remaining graph connected. To show this, Sumner finds a pair of vertices u and v that are as far apart as possible in the graph, and chooses w to be a neighbor of v that is as far from u as possible; as he shows, neither v nor w can lie on any shortest path from any other node to u, so the removal of v and w leaves the remaining graph connected. Repeatedly removing matched pairs of vertices in this way forms a perfect matching in the given claw-free graph.
The same proof idea holds more generally if u is any vertex, v is any vertex that is maximally far from u, and w is any neighbor of v that is maximally far from u. Further, the removal of v and w from the graph does not change any of the other distances from u. Therefore, the process of forming a matching by finding and removing pairs vw that are maximally far from u may be performed by a single postorder traversal of a breadth first search tree of the graph, rooted at u, in linear time. provide an alternative linear-time algorithm based on depth-first search
Depth-first search
Depth-first search is an algorithm for traversing or searching a tree, tree structure, or graph. One starts at the root and explores as far as possible along each branch before backtracking....
, as well as efficient parallel algorithm
Parallel algorithm
In computer science, a parallel algorithm or concurrent algorithm, as opposed to a traditional sequential algorithm, is an algorithm which can be executed a piece at a time on many different processing devices, and then put back together again at the end to get the correct result.Some algorithms...
s for the same problem.
list several related results, including the following: (r − 1)-connected K1,r-free graphs of even order have perfect matchings for any r ≥ 2; claw-free graphs of odd order with at most one degree-one vertex may be partitioned into an odd cycle and a matching; for any k that is at most half the minimum degree of a claw-free graph in which either k or the number of vertices is even, the graph has a k-factor; and, if a claw-free graph is (2k + 1)-connected, then any k-edge matching can be extended to a perfect matching.
Independent sets

Independent set (graph theory)
In graph theory, an independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I...
in a line graph corresponds to a matching in its underlying graph, a set of edges no two of which share an endpoint. As showed, a maximum matching in any graph may be found in polynomial time; extended this algorithm to one that computes a maximum independent set in any claw-free graph. (corrected by ) independently provided an alternative extension of Edmonds' algorithms to claw-free graphs, that transforms the problem into one of finding a matching in an auxiliary graph derived from the input claw-free graph. Minty's approach may also be used to solve in polynomial time the more general problem of finding an independent set of maximum weight, and generalizations of these results to wider classes of graphs are also known.
As Sbihi observed, if I is an independent set in a claw-free graph, then any vertex of the graph may have at most two neighbors in I: three neighbors would form a claw. Sbihi calls a vertex saturated if it has two neighbors in I and unsaturated if it is not in I but has fewer than two neighbors in I. It follows from Sbihi's observation that if I and J are both independent sets, the graph induced by I ∪ J must have degree at most two; that is, it is a union of paths and cycles.
In particular, if I is a non-maximum independent set, it differs from any maximum independent set by cycles and augmenting paths, induced path
Induced path
In the mathematical area of graph theory, an induced path in an undirected graph G is a path that is an induced subgraph of G. That is, it is a sequence of vertices in G such that each two adjacent vertices in the sequence are connected by an edge in G, and each two nonadjacent vertices in the...
s which alternate between vertices in I and vertices not in I, and for which both endpoints are unsaturated. The symmetric difference of I with an augmenting path is a larger independent set; Sbihi's algorithm repeatedly increases the size of an independent set by searching for augmenting paths until no more can be found.
Searching for an augmenting path is complicated by the fact that a path may fail to be augmenting if it contains an edge between two vertices that are not in I, so that it is not an induced path. Fortunately, this can only happen in two cases: the two adjacent vertices may be the endpoints of the path, or they may be two steps away from each other; any other adjacency would lead to a claw. Adjacent endpoints may be avoided by temporarily removing the neighbors of v when searching for a path starting from a vertex v; if no path is found, v can be removed from the graph for the remainder of the algorithm. Although Sbihi does not describe it in these terms, the problem remaining after this reduction may be described in terms of a switch graph
Skew-symmetric graph
In graph theory, a branch of mathematics, a skew-symmetric graph is a directed graph that is isomorphic to its own transpose graph, the graph formed by reversing all of its edges. The isomorphism is required to be an involution without any fixed points....
, an undirected graph in which the edges incident to each vertex are partitioned into two subsets and in which paths through the vertex are constrained to use one edge from each subset. One may form a switch graph that has as its vertices the unsaturated and saturated vertices of the given claw-free graph, with an edge between two vertices of the switch graph whenever they are nonadjacent in the claw-free graph and there exists a length-two path between them that passes through a vertex of I. The two subsets of edges at each vertex are formed by the two vertices of I that these length-two paths pass through. A path in this switch graph between two unsaturated vertices corresponds to an augmenting path in the original graph. The switch graph has quadratic complexity, paths in it may be found in linear time, and O(n) augmenting paths may need to be found over the course of the overall algorithm. Therefore, Sbihi's algorithm runs in O(n3) total time.
Coloring, cliques, and domination
A perfect graphPerfect graph
In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....
is a graph in which the chromatic number and the size of the maximum clique are equal, and in which this equality persists in every induced subgraph. It is now known (the strong perfect graph theorem) that perfect graphs may be characterized as the graphs that do not have as induced subgraphs either an odd cycle or the complement of an odd cycle (a so-called odd hole). However, for many years this remained an unsolved conjecture, only proven for special subclasses of graphs. One of these subclasses was the family of claw-free graphs: it was discovered by several authors that claw-free graphs without odd cycles and odd holes are perfect. Perfect claw-free graphs may be recognized in polynomial time. In a perfect claw-free graph, the neighborhood of any vertex forms the complement of a bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
. It is possible to color
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
perfect claw-free graphs, or to find maximum cliques in them, in polynomial time.
If a claw-free graph is not perfect, it is NP-hard to find to find its largest clique. It is also NP-hard to find an optimal coloring of the graph, because (via line graphs) this problem generalizes the NP-hard problem of computing the chromatic index of a graph. For the same reason, it is NP-hard to find a coloring that achieves an approximation ratio better than 4/3. However, an approximation ratio of two can be achieved by a greedy coloring
Greedy coloring
In the study of graph coloring problems in mathematics and computer science, a greedy coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color...
algorithm, because the chromatic number of a claw-free graph is greater than half its maximum degree.
Although not every claw-free graph is perfect, claw-free graphs satisfy another property, related to perfection. A graph is called domination perfect if it has a minimum dominating set
Dominating set
In graph theory, a dominating set for a graph G = is a subset D of V such that every vertex not in D is joined to at least one member of D by some edge...
that is independent, and if the same property holds in all of its induced subgraphs. Claw-free graphs have this property. To see this, let D be a dominating set in a claw-free graph, and suppose that v and w are two adjacent vertices in D; then the set of vertices dominated by v but not by w must be a clique (else v would be the center of a claw). If every vertex in this clique is already dominated by at least one other member of D, then v can be removed producing a smaller independent dominating set, and otherwise v can be replaced by one of the undominated vertices in its clique producing a dominating set with fewer adjacencies. By repeating this replacement process one eventually reaches a dominating set no larger than D, so in particular when the starting set D is a minimum dominating set this process forms an equally small independent dominating set.
Despite this domination perfectness property, it is NP-hard to determine the size of the minimum dominating set in a claw-free graph. However, in contrast to the situation for more general classes of graphs, finding the minimum dominating set or the minimum connected dominating set in a claw-free graph is fixed-parameter tractable
Parameterized complexity
Parameterized complexity is a branch of computational complexity theory in computer science that focuses on classifying computational problems according to their inherent difficulty with respect to multiple parameters of the input. The complexity of a problem is then measured as a function in those...
: it can be solved in time bounded by a polynomial in the size of the graph multiplied by an exponential function of the dominating set size.
Structure
overview a series of papers in which they prove a structure theory for claw-free graphs, analogous to the graph structure theoremGraph structure theorem
In mathematics, the graph structure theorem is a major result in the area of graph theory. The result establishes a deep and fundamental connection between the theory of graph minors and topological embeddings. The theorem is stated in the seventeenth of a series of 23 papers by Neil Robertson and...
for minor-closed graph families proven by Robertson and Seymour, and to the structure theory for perfect graphs that Chudnovsky, Seymour and their co-authors used to prove the strong perfect graph theorem. The theory is too complex to describe in detail here, but to give a flavor of it, it suffices to outline two of their results. First, for a special subclass of claw-free graphs which they call quasi-line graphs (equivalently, locally co-bipartite graphs), they state that every such graph has one of two forms:
- A fuzzy circular interval graph, a class of graphs represented geometrically by points and arcs on a circle, generalizing proper circular arc graphs.
- A graph constructed from a multigraph by replacing each edge by a fuzzy linear interval graph. This generalizes the construction of a line graph, in which every edge of the multigraph is replaced by a vertex. Fuzzy linear interval graphs are constructed in the same way as fuzzy circular interval graphs, but on a line rather than on a circle.
Chudnovsky and Seymour classify arbitrary connected claw-free graphs into one of the following:
- Six specific subclasses of claw-free graphs. Three of these are line graphs, proper circular arc graphs, and the induced subgraphs of an icosahedron; the other three involve additional definitions.
- Graphs formed in four simple ways from smaller claw-free graphs.
- Antiprismatic graphs, a class of dense graphDense graphIn mathematics, a dense graph is a graph in which the number of edges is close to the maximal number of edges. The opposite, a graph with only a few edges, is a sparse graph...
s defined as the claw-free graphs in which every four vertices induce a subgraph with at least two edges.
Much of the work in their structure theory involves a further analysis of antiprismatic graphs. The Schläfli graph
Schläfli graph
In the mathematical field of graph theory, the Schläfli graph, named after Ludwig Schläfli, is a 16-regular undirected graph with 27 vertices and 216 edges. It is a strongly regular graph with parameters srg.-Construction:...
, a claw-free strongly regular graph
Strongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
with parameters srg(27,16,10,8), plays an important role in this part of the analysis. This structure theory has led to new advances in polyhedral combinatorics
Polyhedral combinatorics
Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing the faces of convex polyhedra and higher dimensional convex polytopes....
and new bounds on the chromatic number of claw-free graphs, as well as to new fixed-parameter-tractable algorithms for dominating sets in claw-free graphs.
External links
- Claw-free graphs, Information System on Graph Class Inclusions

