Triangle-free graph
Encyclopedia
In the mathematical
area of graph theory
, a triangle-free graph is an undirected graph in which no three vertices form a triangle
of edges. Triangle-free graphs may be equivalently defined as graphs with clique number
≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle
, or locally independent
graphs.
By Turán's theorem
, the n-vertex triangle-free graph with the maximum number of edges is a complete bipartite graph
in which the numbers of vertices on each side of the bipartition are as equal as possible.
It is possible to test whether a graph with m edges is triangle-free in time O(m1.41) . Another approach is to find the trace
of A3, where A is the adjacency matrix
of the graph. The trace is zero if and only if the graph is triangle-free. For dense graphs, it is more efficient to use this simple algorithm which relies on matrix multiplication
, since it gets the time complexity down to O(n2.373), where n is the number of vertices.
As show, triangle-free graph recognition is equivalent in complexity to median graph
recognition; however, the current best algorithms for median graph recognition use triangle detection as a subroutine rather than vice versa.
The decision tree complexity or query complexity of the problem, where the queries are to an oracle which stores the adjacency matrix of a graph, is Θ(n2). However, for quantum algorithm
s, the best known lower bound is Ω(n), but the best known algorithm is O(n1.29) due to .
of √n vertices in an n-vertex triangle-free graph is easy to find: either there is a vertex with √n neighbors (in which case those neighbors are an independent set) or all vertices have fewer than √n neighbors (in which case any maximal independent set
must have at least √n vertices). This bound can be tightened slightly: in every triangle-free graph there exists an independent set of
vertices, and in some triangle-free graphs every independent set has 
vertices . One way to generate triangle-free graphs in which all independent sets are small is the triangle-free process in which one generates a maximal triangle-free graph by repeatedly adding randomly chosen edges that do not complete a triangle. With high probability, this process produces a graph with independence number 
. It is also possible to find regular graph
s with the same properties .
These results may also be interpreted as giving asymptotic bounds on the Ramsey numbers R(3,t) of the form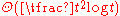
: if the edges of a complete graph on 
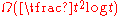vertices are colored red and blue, then either the red graph contains a triangle or, if it is triangle-free, then it must have an independent set of size t corresponding to a clique of the same size in the blue graph.
. Every bipartite graph
(that is, every 2-colorable graph) is triangle-free, and Grötzsch's theorem
states that every triangle-free planar graph
may be 3-colored . However, nonplanar triangle-free graphs may require many more than three colors.
defined a construction, now called the Mycielskian
, for forming a new triangle-free graph from another triangle-free graph. If a graph has chromatic number k, its Mycielskian has chromatic number k + 1, so this construction may be used to show that arbitrarily large numbers of colors may be needed to color nonplanar triangle-free graphs. In particular the Grötzsch graph
, an 11-vertex graph formed by repeated application of Mycielski's construction, is a triangle-free graph that cannot be colored with fewer than four colors, and is the smallest graph with this property . showed that the number of colors needed to color any m-edge triangle-free graph is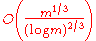
and that there exist triangle-free graphs that have chromatic numbers proportional to this bound.
There have also been several results relating coloring to minimum degree in triangle-free graphs. proved that any n-vertex triangle-free graph in which each vertex has more than 2n/5 neighbors must be bipartite. This is the best possible result of this type, as the 5-cycle requires three colors but has exactly 2n/5 neighbors per vertex. Motivated by this result, conjectured that any n-vertex triangle-free graph in which each vertex has at least n/3 neighbors can be colored with only three colors; however, disproved this conjecture by finding a counterexample in which each vertex of the Grötzsch graph is replaced by an independent set of a carefully chosen size. showed that any n-vertex triangle-free graph in which each vertex has more than 10n/29 neighbors must be 3-colorable; this is the best possible result of this type, because Häggkvist's graph requires four colors and has exactly 10n/29 neighbors per vertex. Finally, proved that any n-vertex triangle-free graph in which each vertex has more than n/3 neighbors must be 4-colorable. Additional results of this type are not possible, as Hajnal (see ) found examples of triangle-free graphs with arbitrarily large chromatic number and minimum degree (1/3 − ε)n for any ε > 0.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
area of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a triangle-free graph is an undirected graph in which no three vertices form a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
of edges. Triangle-free graphs may be equivalently defined as graphs with clique number
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle
Induced path
In the mathematical area of graph theory, an induced path in an undirected graph G is a path that is an induced subgraph of G. That is, it is a sequence of vertices in G such that each two adjacent vertices in the sequence are connected by an edge in G, and each two nonadjacent vertices in the...
, or locally independent
Neighbourhood (graph theory)
In graph theory, an adjacent vertex of a vertex v in a graph is a vertex that is connected to v by an edge. The neighbourhood of a vertex v in a graph G is the induced subgraph of G consisting of all vertices adjacent to v and all edges connecting two such vertices. For example, the image shows a...
graphs.
By Turán's theorem
Turán's theorem
In graph theory, Turán's theorem is a result on the number of edges in a Kr+1-free graph.An n-vertex graph that does not contain any -vertex clique may be formed by partitioning the set of vertices into r parts of equal or nearly-equal size, and connecting two vertices by an edge whenever they...
, the n-vertex triangle-free graph with the maximum number of edges is a complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
in which the numbers of vertices on each side of the bipartition are as equal as possible.
Triangle finding problem
The triangle finding problem is the problem of determining whether a graph is triangle-free or not. When the graph does contain a triangle, algorithms are often required to output three vertices which form a triangle in the graph.It is possible to test whether a graph with m edges is triangle-free in time O(m1.41) . Another approach is to find the trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
of A3, where A is the adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
of the graph. The trace is zero if and only if the graph is triangle-free. For dense graphs, it is more efficient to use this simple algorithm which relies on matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
, since it gets the time complexity down to O(n2.373), where n is the number of vertices.
As show, triangle-free graph recognition is equivalent in complexity to median graph
Median graph
In mathematics, and more specifically graph theory, a median graph is an undirected graph in which any three vertices a, b, and c have a unique median: a vertex m that belongs to shortest paths between any two of a, b, and c.The concept of median graphs has long been studied, for instance by or ...
recognition; however, the current best algorithms for median graph recognition use triangle detection as a subroutine rather than vice versa.
The decision tree complexity or query complexity of the problem, where the queries are to an oracle which stores the adjacency matrix of a graph, is Θ(n2). However, for quantum algorithm
Quantum algorithm
In quantum computing, a quantum algorithm is an algorithm which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a...
s, the best known lower bound is Ω(n), but the best known algorithm is O(n1.29) due to .
Independence number and Ramsey theory
An independent setIndependent set (graph theory)
In graph theory, an independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I...
of √n vertices in an n-vertex triangle-free graph is easy to find: either there is a vertex with √n neighbors (in which case those neighbors are an independent set) or all vertices have fewer than √n neighbors (in which case any maximal independent set
Maximal independent set
In graph theory, a maximal independent set or maximal stable set is an independent set that is not a subset of any other independent set. That is, it is a set S such that every edge of the graph has at least one endpoint not in S and every vertex not in S has at least one neighbor in S...
must have at least √n vertices). This bound can be tightened slightly: in every triangle-free graph there exists an independent set of
vertices, and in some triangle-free graphs every independent set has vertices . One way to generate triangle-free graphs in which all independent sets are small is the triangle-free process in which one generates a maximal triangle-free graph by repeatedly adding randomly chosen edges that do not complete a triangle. With high probability, this process produces a graph with independence number . It is also possible to find regular graphRegular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
s with the same properties .
These results may also be interpreted as giving asymptotic bounds on the Ramsey numbers R(3,t) of the form
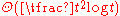: if the edges of a complete graph on 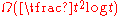vertices are colored red and blue, then either the red graph contains a triangle or, if it is triangle-free, then it must have an independent set of size t corresponding to a clique of the same size in the blue graph.Coloring triangle-free graphs
Much research about triangle-free graphs has focused on graph coloringGraph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
. Every bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
(that is, every 2-colorable graph) is triangle-free, and Grötzsch's theorem
Grötzsch's theorem
In the mathematical field of graph theory, Grötzsch's theorem is the statement that every triangle-free planar graph can be colored with only three colors...
states that every triangle-free planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
may be 3-colored . However, nonplanar triangle-free graphs may require many more than three colors.
defined a construction, now called the Mycielskian
Mycielskian
In the mathematical area of graph theory, the Mycielskian or Mycielski graph of an undirected graph G is a graph μ formed from G by a construction of , who used it to show that there exist triangle-free graphs with arbitrarily large chromatic number.-Construction:Let the n vertices of the given...
, for forming a new triangle-free graph from another triangle-free graph. If a graph has chromatic number k, its Mycielskian has chromatic number k + 1, so this construction may be used to show that arbitrarily large numbers of colors may be needed to color nonplanar triangle-free graphs. In particular the Grötzsch graph
Grötzsch graph
In the mathematical field of graph theory, the Grötzsch graph is a triangle-free graph with 11 vertices, 20 edges, and chromatic number 4. It is named after German mathematician Herbert Grötzsch, and its existence demonstrates that the assumption of planarity is necessary in Grötzsch's theorem ...
, an 11-vertex graph formed by repeated application of Mycielski's construction, is a triangle-free graph that cannot be colored with fewer than four colors, and is the smallest graph with this property . showed that the number of colors needed to color any m-edge triangle-free graph is
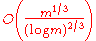
and that there exist triangle-free graphs that have chromatic numbers proportional to this bound.
There have also been several results relating coloring to minimum degree in triangle-free graphs. proved that any n-vertex triangle-free graph in which each vertex has more than 2n/5 neighbors must be bipartite. This is the best possible result of this type, as the 5-cycle requires three colors but has exactly 2n/5 neighbors per vertex. Motivated by this result, conjectured that any n-vertex triangle-free graph in which each vertex has at least n/3 neighbors can be colored with only three colors; however, disproved this conjecture by finding a counterexample in which each vertex of the Grötzsch graph is replaced by an independent set of a carefully chosen size. showed that any n-vertex triangle-free graph in which each vertex has more than 10n/29 neighbors must be 3-colorable; this is the best possible result of this type, because Häggkvist's graph requires four colors and has exactly 10n/29 neighbors per vertex. Finally, proved that any n-vertex triangle-free graph in which each vertex has more than n/3 neighbors must be 4-colorable. Additional results of this type are not possible, as Hajnal (see ) found examples of triangle-free graphs with arbitrarily large chromatic number and minimum degree (1/3 − ε)n for any ε > 0.