Quantum algorithm
Encyclopedia
In quantum computing, a quantum algorithm is an algorithm
which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit
model of computation. A classical (or non-quantum) algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a problem, where each step or instruction can be performed on a classical computer
. Similarly, a quantum algorithm is a step-by-step procedure, where each of the steps can be performed on a quantum computer
. Although all classical algorithms can also be performed on a quantum computer, the term quantum algorithm is usually used for those algorithms which seem inherently quantum, or use some essential feature of quantum computation such as quantum superposition
or quantum entanglement
.
All problems which can be solved on a quantum computer can be solved on a classical computer. In particular, problems which are undecidable
using classical computers remain undecidable using quantum computers. What makes quantum algorithms interesting is that they might be able to solve some problems faster than classical algorithms.
The most well known algorithms are Shor's algorithm
for factoring, and Grover's algorithm
for searching an unstructured database or an unordered list. Shor's algorithms runs exponentially faster than the best known classical algorithm for factoring, the general number field sieve
. Grover's algorithm runs quadratically faster than the best possible classical algorithm for the same task.
which acts on some input qubit
s and terminates with a measurement
. A quantum circuit consists of simple quantum gate
s which act on at most a fixed number of qubits, usually 2 or 3. Quantum algorithms may also be stated in other models of quantum computation, such as the Hamiltonian oracle model.
Quantum algorithms can be categorized by the main techniques used by the algorithm. Some commonly used techniques/ideas in quantum algorithms include phase kick-back, phase estimation
, the quantum Fourier transform
, quantum walks, amplitude amplification
and topological quantum field theory
. Quantum algorithms may also be grouped by the type of problem solved, for instance see the survey on quantum algorithms for algebraic problems.
is the quantum analogue of the discrete Fourier transform
, and is used in several quantum algorithms. The Hadamard transform
is also an example of a quantum Fourier transform over an n-dimensional vector space over the field F2. The quantum Fourier transform can be efficiently implemented on a quantum computer using only a polynomial number of quantum gate
s.
problem and the integer factorization
problem in polynomial time, whereas the best known classical algorithms take super-polynomial time. These problems are not known to be in P
or NP-complete
. It is also one of the few quantum algorithms that solves a non–black-box problem in polynomial time where the best-known classical algorithms run in super-polynomial time.
hidden subgroup problem
is a generalization of many problems that can be solved by a quantum computer, such as Simon's problem, solving Pell's equation
, testing the principal ideal
of a ring
R and factoring
. There are efficient quantum algorithms known for the Abelian hidden subgroup problem. The more general hidden subgroup problem, where the group isn't necessarily abelian, is a generalization of the previously-mentioned problems and graph isomorphism
and certain lattice problems
. Efficient quantum algorithms are known for certain non-abelian groups. However, no efficient algorithms are known for the symmetric group
, which would give an efficient algorithm for graph isomorphis and the dihedral group
, which would solve certain lattice problems.
is a type of exponential sum
. The best known classical algorithm for estimating these sums takes exponential time. Since the discrete logarithm problem reduces to Gauss sum estimation, an efficient classical algorithm for estimating Gauss sums would imply an efficient classical algorithm for computing discrete logarithms, which is considered unlikely. However, quantum computers can estimate Gauss sums to polynomial precision in polynomial time.
consisting of n random Boolean functions mapping n-bit strings to a Boolean value. We are required to find n n-bit strings z1,..., zn such that for the Hadamard-Fourier transform, at least 3/4 of the strings satisfy
and at least 1/4 satisfies
.
This can be done in BQP
.
is a technique that allows the amplification of a chosen subspace of a quantum state. Applications of amplitude amplification usually lead to quadratic speedups over the corresponding classical algorithms. It can be considered to be a generalization of Grover's algorithm.
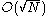queries instead of the Ω(N) queries required classically. Classically, Ω(N) queries are required, even if we allow bounded-error probabilistic algorithms.
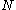-element list, with error 
making only 
queries, where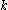 
is the number of marked elements in the list. More precisely, the algorithm outputs an estimate 
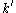for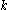 
, the number of marked entries, with the following accuracy: 
.
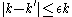. Similar to a classical random walk, which can be described by a probability distribution
over some states, a quantum walk can be described by a quantum superposition
over states. Quantum walks are known to give exponential speedups for some black-box problems. They also provide polynomial speedups for many problems. A framework for the creation quantum walk algorithms exists and is quite a versatile tool.
queries on a quantum computer. The optimal algorithm is by Andris Ambainis
. Scott Aaronson
and Yaoyun Shi first proved a tight lower bound for a large but restricted class of functions. Ambainis and Kutin independently (and via different proofs) extended their work to obtain the lower bound for all functions.
of size 3). The best-known lower bound for quantum algorithms is Ω(N), but the best algorithm known requires O(N1.3) queries.
A well studied formula is the balanced binary tree with only NAND gates. This type of formula requires Θ(Nc) queries using randomness (where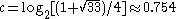
), but can be solved in Θ(N0.5) queries by a quantum algorithm. No better quantum algorithm for this case was known until one was found for the unconventional Hamiltonian oracle model. The same result for the standard setting soon followed.
Fast quantum algorithms for more complicated formulas are also known.
, given by k generators, is commutative
. A black box group is a group with an oracle function, which must be used to perform the group operations (multiplication, inversion, and comparison with identity). We are interested in the query complexity, which is the number of oracle calls needed to solve the problem. The deterministic and randomized query complexities are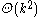
and 
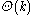respectively. A quantum algorithm requires 
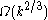queries but the best known algorithm uses 
queries.
can be solved in terms of Jones polynomials. A quantum computer can simulate a TQFT, and thereby approximate the Jones polynomial, which as far as we know, is hard to compute classically in the worst case scenario.
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit
Quantum circuit
In quantum information theory, a quantum circuit is a model for quantum computation in which a computation is a sequence of quantum gates, which are reversible transformations on a quantum mechanical analog of an n-bit register...
model of computation. A classical (or non-quantum) algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a problem, where each step or instruction can be performed on a classical computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
. Similarly, a quantum algorithm is a step-by-step procedure, where each of the steps can be performed on a quantum computer
Quantum computer
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
. Although all classical algorithms can also be performed on a quantum computer, the term quantum algorithm is usually used for those algorithms which seem inherently quantum, or use some essential feature of quantum computation such as quantum superposition
Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
or quantum entanglement
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
.
All problems which can be solved on a quantum computer can be solved on a classical computer. In particular, problems which are undecidable
Undecidable problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
using classical computers remain undecidable using quantum computers. What makes quantum algorithms interesting is that they might be able to solve some problems faster than classical algorithms.
The most well known algorithms are Shor's algorithm
Shor's algorithm
Shor's algorithm, named after mathematician Peter Shor, is a quantum algorithm for integer factorization formulated in 1994...
for factoring, and Grover's algorithm
Grover's algorithm
Grover's algorithm is a quantum algorithm for searching an unsorted database with N entries in O time and using O storage space . It was invented by Lov Grover in 1996....
for searching an unstructured database or an unordered list. Shor's algorithms runs exponentially faster than the best known classical algorithm for factoring, the general number field sieve
General number field sieve
In number theory, the general number field sieve is the most efficient classical algorithm known for factoring integers larger than 100 digits...
. Grover's algorithm runs quadratically faster than the best possible classical algorithm for the same task.
Overview
Quantum algorithms are usually described, in the commonly-used circuit model of quantum computation, by a quantum circuitQuantum circuit
In quantum information theory, a quantum circuit is a model for quantum computation in which a computation is a sequence of quantum gates, which are reversible transformations on a quantum mechanical analog of an n-bit register...
which acts on some input qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s and terminates with a measurement
Measurement
Measurement is the process or the result of determining the ratio of a physical quantity, such as a length, time, temperature etc., to a unit of measurement, such as the metre, second or degree Celsius...
. A quantum circuit consists of simple quantum gate
Quantum gate
In quantum computing and specifically the quantum circuit model of computation, a quantum gate is a basic quantum circuit operating on a small number of qubits. They are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits.Unlike many classical...
s which act on at most a fixed number of qubits, usually 2 or 3. Quantum algorithms may also be stated in other models of quantum computation, such as the Hamiltonian oracle model.
Quantum algorithms can be categorized by the main techniques used by the algorithm. Some commonly used techniques/ideas in quantum algorithms include phase kick-back, phase estimation
Quantum phase estimation algorithm
In quantum computing, the quantum phase estimation algorithm is a quantum algorithm that finds many applications as a subroutine in other algorithms...
, the quantum Fourier transform
Quantum Fourier transform
In quantum computing, the quantum Fourier transform is a linear transformation on quantum bits, and is the quantum analogue of the discrete Fourier transform...
, quantum walks, amplitude amplification
Amplitude amplification
Amplitude amplification is a technique in quantum computing which generalizes the idea behindthe Grover's search algorithm, and gives rise to a family ofquantum algorithms.It was discovered by Gilles Brassard andPeter Høyer in 1997,...
and topological quantum field theory
Topological quantum field theory
A topological quantum field theory is a quantum field theory which computes topological invariants....
. Quantum algorithms may also be grouped by the type of problem solved, for instance see the survey on quantum algorithms for algebraic problems.
Algorithms based on the quantum Fourier transform
The quantum Fourier transformQuantum Fourier transform
In quantum computing, the quantum Fourier transform is a linear transformation on quantum bits, and is the quantum analogue of the discrete Fourier transform...
is the quantum analogue of the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
, and is used in several quantum algorithms. The Hadamard transform
Hadamard transform
The Hadamard transform is an example of a generalized class of Fourier transforms...
is also an example of a quantum Fourier transform over an n-dimensional vector space over the field F2. The quantum Fourier transform can be efficiently implemented on a quantum computer using only a polynomial number of quantum gate
Quantum gate
In quantum computing and specifically the quantum circuit model of computation, a quantum gate is a basic quantum circuit operating on a small number of qubits. They are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits.Unlike many classical...
s.
Deutsch–Jozsa algorithm
The Deutsch–Jozsa algorithm solves a black-box problem which provably requires exponentially many queries to the black box for any deterministic classical computer, but can be done with exactly 1 query by a quantum computer. If we allow both bounded-error quantum and classical algorithms, then there is no speedup since a classical probabilistic algorithm can solve the problem with a constant number of queries with small probability of error.Simon's algorithm
Simon's algorithm solves a black-box problem exponentially faster than any classical algorithm, including bounded-error probabilistic algorithms. This algorithm, which achieves an exponential speedup over all classical algorithms that we consider efficient, was the motivation for Shor's factoring algorithm.Shor's algorithm
Shor's algorithm solves the discrete logarithmDiscrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
problem and the integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
problem in polynomial time, whereas the best known classical algorithms take super-polynomial time. These problems are not known to be in P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
or NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
. It is also one of the few quantum algorithms that solves a non–black-box problem in polynomial time where the best-known classical algorithms run in super-polynomial time.
Hidden subgroup problem
The abelianAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
hidden subgroup problem
Hidden subgroup problem
The hidden subgroup problem is a topic of research in mathematics and theoretical computer science.-Problem statement:Given a group G, a subgroup H ≤ G, and a set X, we say a function f : G → X hides the subgroup H if for all g1, g2 ∈ G,f = f if and only if g1H = g2H for the cosets of...
is a generalization of many problems that can be solved by a quantum computer, such as Simon's problem, solving Pell's equation
Pell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
, testing the principal ideal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
of a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R and factoring
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
. There are efficient quantum algorithms known for the Abelian hidden subgroup problem. The more general hidden subgroup problem, where the group isn't necessarily abelian, is a generalization of the previously-mentioned problems and graph isomorphism
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
and certain lattice problems
Lattice problems
In computer science, lattice problems are a class of optimization problems on lattices. The conjectured intractability of such problems is central to construction of secure lattice-based cryptosystems...
. Efficient quantum algorithms are known for certain non-abelian groups. However, no efficient algorithms are known for the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
, which would give an efficient algorithm for graph isomorphis and the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
, which would solve certain lattice problems.
Estimating Gauss sums
A Gauss sumGauss sum
In mathematics, a Gauss sum or Gaussian sum is a particular kind of finite sum of roots of unity, typicallyG := G= \sum \chi\cdot \psi...
is a type of exponential sum
Exponential sum
In mathematics, an exponential sum may be a finite Fourier series , or other finite sum formed using the exponential function, usually expressed by means of the functione = \exp.\,...
. The best known classical algorithm for estimating these sums takes exponential time. Since the discrete logarithm problem reduces to Gauss sum estimation, an efficient classical algorithm for estimating Gauss sums would imply an efficient classical algorithm for computing discrete logarithms, which is considered unlikely. However, quantum computers can estimate Gauss sums to polynomial precision in polynomial time.
Fourier fishing and Fourier checking
We have an oracleOracle
In Classical Antiquity, an oracle was a person or agency considered to be a source of wise counsel or prophetic predictions or precognition of the future, inspired by the gods. As such it is a form of divination....
consisting of n random Boolean functions mapping n-bit strings to a Boolean value. We are required to find n n-bit strings z1,..., zn such that for the Hadamard-Fourier transform, at least 3/4 of the strings satisfy
and at least 1/4 satisfies
.This can be done in BQP
BQP
In computational complexity theory BQP is the class of decision problems solvable by a quantum computer in polynomial time, with an error probability of at most 1/3 for all instances...
.
Algorithms based on amplitude amplification
Amplitude amplificationAmplitude amplification
Amplitude amplification is a technique in quantum computing which generalizes the idea behindthe Grover's search algorithm, and gives rise to a family ofquantum algorithms.It was discovered by Gilles Brassard andPeter Høyer in 1997,...
is a technique that allows the amplification of a chosen subspace of a quantum state. Applications of amplitude amplification usually lead to quadratic speedups over the corresponding classical algorithms. It can be considered to be a generalization of Grover's algorithm.
Grover's algorithm
Grover's algorithm searches an unstructured database (or an unordered list) with N entries, for a marked entry, using only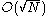 queries instead of the Ω(N) queries required classically. Classically, Ω(N) queries are required, even if we allow bounded-error probabilistic algorithms.Quantum counting
Quantum counting solves a generalization of the search problem. It solves the problem of counting the number of marked entries in an unordered list, instead of just detecting if one exists. Specifically, it counts the number of marked entries in an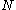-element list, with error making only queries, where 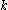is the number of marked elements in the list. More precisely, the algorithm outputs an estimate 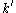for 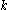, the number of marked entries, with the following accuracy: 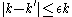.Algorithms based on quantum walks
A quantum walk is the quantum analogue of a classical random walkRandom walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
. Similar to a classical random walk, which can be described by a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
over some states, a quantum walk can be described by a quantum superposition
Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
over states. Quantum walks are known to give exponential speedups for some black-box problems. They also provide polynomial speedups for many problems. A framework for the creation quantum walk algorithms exists and is quite a versatile tool.
Element distinctness problem
The element distinctness problem is the problem of determining whether all the elements of a list are distinct. Classically, Ω(N) queries are required for a list of size N, since this problem is harder than the search problem which requires Ω(N) queries. However, it can be solved in queries on a quantum computer. The optimal algorithm is by Andris AmbainisAndris Ambainis
Andris Ambainis is a Latvian computer scientist active in the fields of quantum information theory and quantum computing. He has held past positions at the Institute for Advanced Study at Princeton, New Jersey and the Institute for Quantum Computing at the University of Waterloo. He is currently a...
. Scott Aaronson
Scott Aaronson
Scott Joel Aaronson is a theoretical computer scientist and faculty member in the Electrical Engineering and Computer Science department at the Massachusetts Institute of Technology.-Education:...
and Yaoyun Shi first proved a tight lower bound for a large but restricted class of functions. Ambainis and Kutin independently (and via different proofs) extended their work to obtain the lower bound for all functions.
Triangle-finding problem
The triangle-finding problem is the problem of determining whether a given graph contains a triangle (a cliqueClique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
of size 3). The best-known lower bound for quantum algorithms is Ω(N), but the best algorithm known requires O(N1.3) queries.
Formula Evaluation
A formula is a tree with a gate at each internal node and an input bit at each leaf node. The problem is to evaluate the formula, which is the output of the root node, given oracle access to the input.A well studied formula is the balanced binary tree with only NAND gates. This type of formula requires Θ(Nc) queries using randomness (where
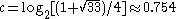), but can be solved in Θ(N0.5) queries by a quantum algorithm. No better quantum algorithm for this case was known until one was found for the unconventional Hamiltonian oracle model. The same result for the standard setting soon followed.Fast quantum algorithms for more complicated formulas are also known.
Group Commutativity
The problem is to determine if a black box groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, given by k generators, is commutative
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
. A black box group is a group with an oracle function, which must be used to perform the group operations (multiplication, inversion, and comparison with identity). We are interested in the query complexity, which is the number of oracle calls needed to solve the problem. The deterministic and randomized query complexities are
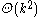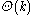and respectively. A quantum algorithm requires 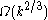queries but the best known algorithm uses queries.Computing knot invariants
Witten had shown that the Chern-Simons topological quantum field theoryTopological quantum field theory
A topological quantum field theory is a quantum field theory which computes topological invariants....
can be solved in terms of Jones polynomials. A quantum computer can simulate a TQFT, and thereby approximate the Jones polynomial, which as far as we know, is hard to compute classically in the worst case scenario.
Quantum Simulation
The idea that quantum computers might be more powerful than classical computers originated in Richard Feynman's observation that classical computers seem to require exponential time to simulate many-particle quantum systems. Since then, the idea that quantum computers can simulate quantum physical processes exponentially faster than classical computers has been greatly fleshed out and elaborated. Efficient (that is, polynomial-time) quantum algorithms have been developed for simulating both Bosonic and Fermionic systems and in particular, the simulation of chemical reactions beyond the capabilities of current classical supercomputers requires only a few hundred qubits. Quantum computers can also efficiently simulate topological quantum field theories. In addition to its intrinsic interest, this result has led to efficient quantum algorithms for estimating "quantum" topological invariants such as Jones and HOMFLY polynomials, and the Turaev-Viro invariant of three-dimensional manifolds.External links
- The Quantum Algorithm Zoo: A comprehensive list of quantum algorithms that provide a speedup over the fastest known classical algorithms.