
Discrete logarithm
Encyclopedia
In mathematics
, specifically in abstract algebra
and its applications, discrete logarithms are group-theoretic
analogues of ordinary logarithm
s. In particular, an ordinary logarithm loga(b) is a solution of the equation ax = b over the real or complex numbers. Similarly, if g and h are elements of a finite cyclic group
G then a solution x of the equation gx = h is called a discrete logarithm to the base g of h in the group G.
. This is the set {1, …, p − 1} of congruence classes under multiplication modulo
the prime
p.
If we want to find the kth power
of one of the numbers in this group, we can do so by finding its kth power as an integer and then finding the remainder after division by p. This process is called discrete exponentiation. For example, consider (Z17)×. To compute 34 in this group, we first compute 34 = 81, and then we divide 81 by 17, obtaining a remainder of 13. Thus 34 = 13 in the group (Z17)×.
Discrete logarithm is just the inverse operation. For example, take the equation 3k ≡ 13 (mod 17) for k. As shown above k=4 is a solution, but it is not the only solution. Since 316 ≡ 1 (mod 17) it also follows that if n is an integer then 34+16 n ≡ 13 × 1n ≡ 13 (mod 17). Hence the equation has infinitely many solutions of the form 4 + 16n. Moreover, since 16 is the smallest positive integer m satisfying 3m ≡ 1 (mod 17), i.e. 16 is the order
of 3 in (Z17)×, these are the only solutions. Equivalently, the solution can be expressed as k ≡ 4 (mod 16).
with n elements. We assume that the group is written multiplicatively. Let b be a generator
of G; then every element g of G can be written in the form g = bk for some integer k. Furthermore, any two such integers k1 and k2 representing g will be congruent modulo
n. We can thus define a function
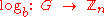
(where Zn denotes the ring of integers modulo n) by assigning to each g the congruence class of k modulo n. This function is a group isomorphism
, called the discrete logarithm to base b.
The familiar base change formula for ordinary logarithms remains valid: If c is another generator of G, then we have
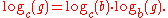
linear in the size of the group G and thus exponential in the number of digits in the size of the group. There exists an efficient quantum algorithm due to Peter Shor
.
More sophisticated algorithms exist, usually inspired by similar algorithms for integer factorization. These algorithms run faster than the naive algorithm, but none of them runs in polynomial time (in the number of digits in the size of the group).
are distinct problems they share some properties:
can be shown to be about as hard as the worst case using random self-reducibility
.
At the same time, the inverse problem of discrete exponentiation is not difficult (it can be computed efficiently using exponentiation by squaring
, for example). This asymmetry is analogous to the one between integer factorization and integer multiplication
. Both asymmetries have been exploited in the construction of cryptographic systems.
Popular choices for the group G in discrete logarithm cryptography
are the cyclic groups (Zp)×; see ElGamal encryption
, Diffie–Hellman key exchange, and the Digital Signature Algorithm
.
Newer cryptography applications use discrete logarithms in cyclic subgroups of elliptic curve
s over finite field
s; see elliptic curve cryptography
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and its applications, discrete logarithms are group-theoretic
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
analogues of ordinary logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
s. In particular, an ordinary logarithm loga(b) is a solution of the equation ax = b over the real or complex numbers. Similarly, if g and h are elements of a finite cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
G then a solution x of the equation gx = h is called a discrete logarithm to the base g of h in the group G.
Example
Discrete logarithms are perhaps simplest to understand in the group (Zp)×Multiplicative group of integers modulo n
In modular arithmetic the set of congruence classes relatively prime to the modulus n form a group under multiplication called the multiplicative group of integers modulo n. It is also called the group of primitive residue classes modulo n. In the theory of rings, a branch of abstract algebra, it...
. This is the set {1, …, p − 1} of congruence classes under multiplication modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
the prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p.
If we want to find the kth power
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
of one of the numbers in this group, we can do so by finding its kth power as an integer and then finding the remainder after division by p. This process is called discrete exponentiation. For example, consider (Z17)×. To compute 34 in this group, we first compute 34 = 81, and then we divide 81 by 17, obtaining a remainder of 13. Thus 34 = 13 in the group (Z17)×.
Discrete logarithm is just the inverse operation. For example, take the equation 3k ≡ 13 (mod 17) for k. As shown above k=4 is a solution, but it is not the only solution. Since 316 ≡ 1 (mod 17) it also follows that if n is an integer then 34+16 n ≡ 13 × 1n ≡ 13 (mod 17). Hence the equation has infinitely many solutions of the form 4 + 16n. Moreover, since 16 is the smallest positive integer m satisfying 3m ≡ 1 (mod 17), i.e. 16 is the order
Multiplicative order
In number theory, given an integer a and a positive integer n with gcd = 1, the multiplicative order of a modulo n is the smallest positive integer k withThe order of a modulo n is usually written ordn, or On.- Example :To determine the multiplicative order of 4 modulo 7, we compute 42 = 16 ≡ 2 ...
of 3 in (Z17)×, these are the only solutions. Equivalently, the solution can be expressed as k ≡ 4 (mod 16).
Definition
In general, let G be a finite cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
with n elements. We assume that the group is written multiplicatively. Let b be a generator
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
of G; then every element g of G can be written in the form g = bk for some integer k. Furthermore, any two such integers k1 and k2 representing g will be congruent modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
n. We can thus define a function
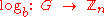
(where Zn denotes the ring of integers modulo n) by assigning to each g the congruence class of k modulo n. This function is a group isomorphism
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
, called the discrete logarithm to base b.
The familiar base change formula for ordinary logarithms remains valid: If c is another generator of G, then we have
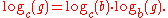
Algorithms
No efficient classical algorithm for computing general discrete logarithms logb g is known. The naive algorithm is to raise b to higher and higher powers k until the desired g is found; this is sometimes called trial multiplication. This algorithm requires running timeRunning Time
Running Time may refer to:* Running Time * see Analysis of algorithms...
linear in the size of the group G and thus exponential in the number of digits in the size of the group. There exists an efficient quantum algorithm due to Peter Shor
Peter Shor
Peter Williston Shor is an American professor of applied mathematics at MIT, most famous for his work on quantum computation, in particular for devising Shor's algorithm, a quantum algorithm for factoring exponentially faster than the best currently-known algorithm running on a classical...
.
More sophisticated algorithms exist, usually inspired by similar algorithms for integer factorization. These algorithms run faster than the naive algorithm, but none of them runs in polynomial time (in the number of digits in the size of the group).
- Baby-step giant-stepBaby-step giant-stepIn group theory, a branch of mathematics, the baby-step giant-step is a meet-in-the-middle algorithm computing the discrete logarithm. The discrete log problem is of fundamental importance to the area of public key cryptography...
- Pollard's rho algorithm for logarithmsPollard's rho algorithm for logarithmsPollard's rho algorithm for logarithms is an algorithm for solving the discrete logarithm problem analogous to Pollard's rho algorithm for solving the Integer factorization problem....
- Pollard's kangaroo algorithm (aka Pollard's lambda algorithm)
- Pohlig–Hellman algorithm
- Index calculus algorithm
- Number field sieve
- Function field sieveFunction field sieveIn mathematics, the function field sieve was introduced in 1994 by Adleman as an efficient technique for extracting discrete logarithms over finite fields of small characteristic, and elaborated by Adleman and Huang in 1999....
Comparison with integer factorization
While the problem of computing discrete logarithms and the problem of integer factorizationInteger factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
are distinct problems they share some properties:
- both problems are difficult (no efficient algorithmAlgorithmIn mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s are known for non-quantum computerQuantum computerA quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
s), - for both problems efficient algorithms on quantum computers are known,
- algorithms from one problem are often adapted to the other, and
- the difficulty of both problems has been utilized to construct various cryptographicCryptographyCryptography is the practice and study of techniques for secure communication in the presence of third parties...
systems.
Cryptography
There exist groups for which computing discrete logarithms is apparently difficult. In some cases (e.g. large prime order subgroups of groups (Zp)×) there is not only no efficient algorithm known for the worst case, but the average-case complexityAverage-case complexity
Average-case complexity is a subfield of computational complexity theory that studies the complexity of algorithms on random inputs.The study of average-case complexity has applications in the theory of cryptography....
can be shown to be about as hard as the worst case using random self-reducibility
Random Self-reducibility
Random self-reducibility is the rule that a good algorithm for the average case implies a good algorithm for the worst case. RSR is the ability to solve all instances of a problem by solving a large fraction of the instances.-Definition:...
.
At the same time, the inverse problem of discrete exponentiation is not difficult (it can be computed efficiently using exponentiation by squaring
Exponentiation by squaring
Exponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add...
, for example). This asymmetry is analogous to the one between integer factorization and integer multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
. Both asymmetries have been exploited in the construction of cryptographic systems.
Popular choices for the group G in discrete logarithm cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
are the cyclic groups (Zp)×; see ElGamal encryption
ElGamal encryption
In cryptography, the ElGamal encryption system is an asymmetric key encryption algorithm for public-key cryptography which is based on the Diffie–Hellman key exchange. It was described by Taher Elgamal in 1984. ElGamal encryption is used in the free GNU Privacy Guard software, recent versions of...
, Diffie–Hellman key exchange, and the Digital Signature Algorithm
Digital Signature Algorithm
The Digital Signature Algorithm is a United States Federal Government standard or FIPS for digital signatures. It was proposed by the National Institute of Standards and Technology in August 1991 for use in their Digital Signature Standard , specified in FIPS 186, adopted in 1993. A minor...
.
Newer cryptography applications use discrete logarithms in cyclic subgroups of elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s over finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s; see elliptic curve cryptography
Elliptic curve cryptography
Elliptic curve cryptography is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S...
.

